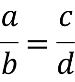Урок математики у 6 класі на тему: "Пропорція. Основна властивість пропорції"

Тема: Пропорція. Основна властивість пропорції.

Мета уроку: сформувати поняття пропорції, ознайомити з основною властивістю пропорції, правилами знаходження її членів; розвивати творчі здібності, пам’ять уміння; виховувати культуру математичної мови, інтерес до нових знань і прагнення їх набути.

Тип уроку: засвоєння нових знань і умінь.

Обладнання. Презентація.

Хід уроку.

 

Девіз уроку:Математику вже навіть задля того потрібно вивчати,що вона розум до ладу приводить.

М.В. Ломоносов

1. Організаційний етап.

Доброго дня, діти!

Дзвоник щойно пролунав,

Нас до класу всіх позвав –

Труд наш знову починаймо!

Тож всім успіхів бажаю!

Перевірте готовність робочих місць. Ми розпочинаємо урок.

2. Перевірка домашнього завдання.

Взаємоперевірка за зразком.

Я задоволена, що всі готові до уроку і маю надію, що він буде для вас цікавим і корисним.

Я бажаю вам знання подвоїти,

Уміння потроїти,

Здібності піднести до квадрата.

А поганий настрій помножити на нуль!

3. Оголошення теми та мети уроку.Мотивація навчального процесу.

У житті  часто трапляються ситуації, коли треба поділити: цукерки, торт, на підприємствах ділять між працівниками премії(залежно від їх внеску у роботу). У всіх цих випадках, коли мова йде про поділ, користуються математичним поняттям «пропорція». Щоб добре засвоїти термін «пропорція» та саме це поняття, потрібно чітко розуміти значення та межі застосування поняття відношення. А на попередніх уроках ми вже вивчили означення та основну властивість відношення. Сьогодні ми розширимо з вами знання про відношення, розглянемо особливості вживання цього терміна в українській мові та вивчимо поняття пропорції, її основну властивість.

 В зошитах запишіть число та тему.

 

4. Актуалізація опорних знань учнів. Так само, як силові тренування тренують наші м’язи, людський мозок, як біцепс, постійно потребує тренування, інакше він дуже швидко втрачає теж «форму» Але як же змусити свій мозок працювати? У цьому нам допоможе математика, її різноманітні й цікаві завдання. Тож будемо тренувати мозок.

Гра «Мозковий штурм»

 

1.Яку назву ми можемо дати записам 2:7 або 12:17? (відношення)

2. Що називається відношенням двох чисел?(частку цих чисел)

3. На що вказує відношення? (У скільки разів одне число більше за інше або яку частину становить одне число від іншого)

4. У скільки разів 6 га більше за 2 га?

5.Чому дорівнює відношення чисел 44 до 11?

5. Вивчення нового матеріалу.

1.Гра «Знайди рівні відношення»

Знайдемо відношення 36 до 9 і 24 до 6.

36:9=24:6

Приклад  18 : 6 = 3 : 1, 21:3=49:7

2.Пояснення нового матеріалу.

         Рівність двох відношень називаються пропорцією.

У нас на черзі ще одна

знань важлива порція.

Така рівність чарівна

На ім’я пропорція.

Слово «пропорція» походить від латинського «proportio», що означає співрозмірність, тобто має правильне співвідношення між частинами і цілими.

Першими відношення та пропорції вивчали давньогрецькі математики. 2500 років тому у Греції існувала математична школа, послідовники якої називали себе Піфагорійцями тому, що засновником цієї школи був Піфагор. Зараз  ми продовжимо вивчати відкриття піфагорійців. Серед них є вчення про пропорції, яке застосовується майже в усіх галузях людської діяльності.

До ХVІ ст.. пропорції записували переважно словесно.

 Г.В.Лейбніц у 1693 році ввів запис за допомогою двокрапки і дорівнює, яким ми й користуємося.

Розглянемо презентацією.

Сьогодні на уроці ми вивчимо:

• Означення пропорції;
• Елементи пропорції;
• Основну  властивість пропорції.

А також навчимося

   застосовувати вивчені властивості для виконання вправ.

1. Означення пропорції

Рівність двох відношень називається пропорцією.

    a : b = c : d         або    

 

2. Елементи пропорції:

 

середні члени пропорції                                    середні члени пропорції

 

          a : b = c : d                             або              

                                         

крайні члени пропорції                                      крайні члени пропорції

3. Основна властивість пропорції

Знайдемо добутки крайніх і середніх членів пропорції 18:6=3:1.

18*1=18; 6*3=18

Добуток крайніх членів пропорції дорівнює добутку її середніх членів.

якщо    a : b = c : d    або                 , то  

                      

                                                                      ad = bc  

 

6. Закріплення нових знань

1.Виконання письмових вправ.

Відомо, що відношення 15 до 5 дорівнює відношенню 18 до деякого числа  х. Чи можна знайти число  х?

Розв’язування:

Перший спосіб.                                                 Спосіб другий.

15 : 5 = 18 : х                                                    15 : 5 = 18 : х

15 : 5 = 3, то 18 : х = 3                                    використавши основну

                        х = 18 : 3                                    властивість пропорції, маємо:

                        х = 6                                           15 ∙ х = 5 ∙ 18

                                                                            х =

Відповідь: 6                                                       Відповідь: 6

2.Робота з підручником  

вправа 552 с.97

вправа 572

3.Пропорція «Золотий переріз».

• Як ви вважаєте, слово «пропорція» суто математичне, чи його можна використовувати в інших галузях? (відповіді учнів).
• Пропорція має багато спільного з музикою, архітектурою, і навіть з природою.  А що саме, нам допоможе розібратися кросворд.

 

4. Розгадування кросворда.

						1
				2
3
					4
					5

 

 

Запитання:

    1. Як називаються члени пропорції а і д?

   2. Як називають у пропорції члени в і с ?

   З. Як називається пропорція, значення лівої і правої частини    якої є одне й те саме число?

   4. У правильній пропорції добуток крайніх членів дорівнює    добутку середніх.  Як називається ця властивість?

   5. Яким математичним терміном    можна замінити слово  «відношення»?

• Отже, це – краса.
• Чому ми захоплені, коли слухаємо музику, читаємо вірші, розглядаємо витвори архітектури, живопису, дивимося на павутинку, на розташування насіння соняшника? Бо все це створено за законами краси. Виявляється, що кришталик людського ока найкраще сприймає предмети, розміри яких перебувають у відношенні 618:1000. Таке відношення називають золотим перерізом. Золотий переріз – гармонічна пропорція. Видатні майстри живопису Леонардо да Вінчі,  Рафаель та інші в основу своїх творінь поклали золоту пропорцію або «золотий переріз». Й. Кеплер говорив, що геометрія володіє двома скарбами – теоремою Піфагора та золотим перерізом.
• Природа – теж справжній знавець пропорцій.
• Щодо пропорції людини. Розміри і форми тіла кожної людини генетично запрограмовані. Під пропорціями тіла маються на увазі співвідношення розмірів окремих частин тіла. І ось що цікаво (деякі доведення):
  • Довжина витягнутих рук дорівнюватиме зросту.
  • Три долоні дорівнюють стопі , шість долонь становлять один лікоть , чотири лікті - зріст людини.

Маса мозку людини становить 1/46 загальної маси тіла .

• Майстри Стародавньої Греції вміло користувалися золотою пропорцією, використовували її гармонічні величини в усіх видах мистецтва і досягли такої досконалості побудови форм, яка рідко зустрічається в практиці світового мистецтва. Вершиною світового мистецтва вважається афінський Парфенон.
•        Учення про відношення і пропорції стародавні греки називали музикою, яку вважали галуззю математики.  Вони знали, що чим слабше натягнуто струну, тим нижчий звук, який вона дає, а чим тугіше натягнуто струну, тим вищий дає вона звук. Але в кожному музичному інструменті є кілька струн.
     Щоб усі струни під час гри звучали приємно для вуха, довжини струн повинні перебувати в певному відношенні. Великий майстер Антоніо Страдіварі використовував співвідношення «золотого перерізу» у своїх знаменитих скрипках . І тому почувши одного разу такі твори хочеться їх слухати, слухати, слухати…… (відео скрипальниці)

1.  

7. Підсумок  уроку.

-Що ми повторили сьогодні ?

Що нового навчилися?

8. Домашнє завдання

 Вивчити п.13. Вправа 558, 561, 577*

 Додаток № 1

Золота пропорція в архітектурі

 

Недарма кажуть, що архітектура - це математика в камені. «Золотий переріз» використовують  архітектори для знаходження гармонійних пропорцій споруд.

Вершиною світового мистецтва вважається шедевр давньогрецької архітектури Парфенон – храм в Афінах, побудований в V столітті до нашої ери. Парфенон підкорює красою форм і закономірністю пропорцій.  Відношення висоти храму до його довжини дорівнює відношенню золотого перерізу.

 

Золотий переріз можна побачити в будівлі  Собора Паризької Богоматері (Собор Нотр-Дам де Пари  в Парижі)

 

Відношення висоти найкрасивіших будівель до їх довжини складає золоту пропорцію. Серед архітектурних шедеврів, які є символом гармонії й архітектурної досконалості хочеться відзначити:

Капелу Пацці у Флоренції Єгипетські піраміди

Будинок із химерами в Києві Храм Софії Київської.

 

Додаток № 2

Золота пропорція в мистецтві

Золота пропорція – головний естетичний принцип у мистецтві.

Золота пропорція або «Золотий переріз» був особливо популярним в епоху Відродження. Цей термін уперше увів Леонардо да Вінчі. Композиція його відомої картини «Мона Ліза» заснована на золотих трикутниках, що являють собою  рівнобедрені трикутники, у яких відношення довжини основи до довжини бічної сторони є золотою пропорцією.

Вибираючи розміри самої картини, художники намагалися, щоб її сторони перебували в золотому відношенні. Такий прямокутник стали називати «золотим».

Прикладом такого прямокутника є картина Сальвадора Далі «Таємна вечеря».

Сальвадор Далі «Таємна вечеря»	І.А. Айвазовський «Італійський пейзаж»

На картинах з пейзажем видатних художників лінія горизонту не проходить по середині полотна. Вона обов'язково ділить його на частини, відношення площ яких є золотою пропорцією... Саме таке відношення виявляється найбільш сприятливим для сприйняття зображення глядачами.

 

Додаток № 3

Золота пропорція в скульптурі

 

Відомо, що ще в давнину основу скульптури складала пропорція. Співвідношення частин людського тіла пов’язувалось з формулою золотого перерізу. Мармурова статуя Венери Мілоської вважається ідеалом краси жіночого тіла, а  статуя Аполлона Бельведерського – ідеалом краси чоловічого тіла. І все тому, що будова тіла людини - теж «золота пропорція».

Скульптори стверджують, що талія ділить довершене людське тіло в співвідношенні «золотого перерізу». Встановлено, що пропорції чоловіків ближче до золотого перерізу, ніж пропорції жінок. І щоб наблизитися до ідеальної золотої пропорції, жінки носять взуття на підборах.

Художники , вчені , модельєри , дизайнери роблять свої розрахунки та креслення, виходячи зі співвідношення "золотого перерізу".

 

Венера Мілоська	Аполлон Бельведерський

 

 

 

 

Додаток № 4

 

1.     Складіть пропорцію з чисел  12; 2;   8;    3

К	Л	М
12:3=8:2	12:8=2:3	2:8=12:3

 

2.     У пропорції 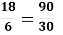 середніми членами є числа…

А	Н	Р
18 і 30	18 і 90	6 і 90

 

3.     У пропорції 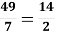крайніми членами є числа…

А	О	У
49 і 2	7 і 14	49 і 14

 

4.     Яка рівність випливає з пропорції 16:12=32:24 відповідно

до основної властивості пропорції

Д	С	Т
16·32=12·24	16·24=12·32	16:32=12:24

 

5.     Знайдіть невідомий член пропорції 36:6=х:5

І	А	Е
25	30	20

 

                

1	2	3	4	5