Урок математики в 6 класі "Побудова точок на координатній площині"

Тема.                        Побудова точок на координатній площині

Мета.                       Відпрацювання навичок побудови точок на координатній площині і вміння  знаходити координати точок, побудованих на площині, формувати вміння застосовувати вивчений матеріал до розв’язування завдань; розвивати пізнавальну активність, творчі здібності, навички самостійної роботи; виховувати інтерес до математики, усвідомленість своїх дій і їх використання в реальному житті

Тип уроку:              формування вмінь та навичок

Обладннання:        екран, мультимедійний проектор, картки з завданнями для самостійної роботи, презентація

Форми та методи:  самостійна робота з використанням мультимедійних матеріалів та    роздаткового матеріалу, колективна форма роботи, проблемно-пошуковий метод

 

Хід уроку

І. Організаційний момент

 

ІІ. Актуалізація опорних знань

 

1. Яку тему ми опрацювали на попередньому уроці?

За допомогою математичного диктанту перевіримо ваші знання з теми «Координатна площина»

2. Математичний диктант (з наступною самоперевіркою)

1. Як називається горизонтальна вісь?

               

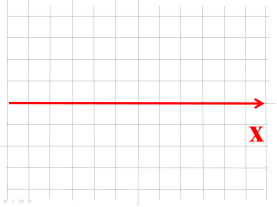
2. Як називається вертикальна вісь?

              

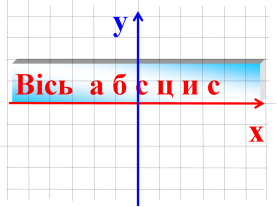
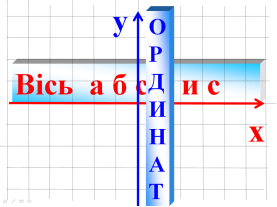
3. Як називається точка перетину числових прямих?

                

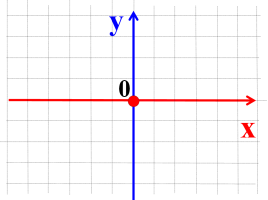
4. Що необхідно додати, щоб утворилась прямокутна система координат?

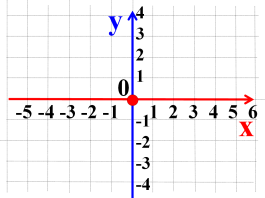
5. Як інакше називають прямокутну систему координат? (Декартова система координат)

Рене Декарт ввів поняття прямокутної системи координат в математику і першим застосував її для розв’язування геометричних завдань.

 

 

 

 

 

6. Скільки чисел необхілно вказати, щоб задати місце знаходження точки на координатній площині? Як вони називаються?

Повторимо як будуються точки за їх координатами.

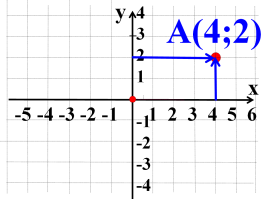
7. Вказати ординати (абсциси) точок

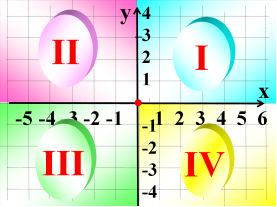
8. Вкажіть нумерацію координатних чвертей.

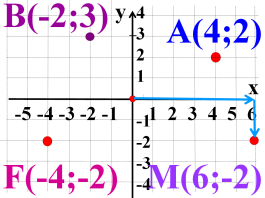
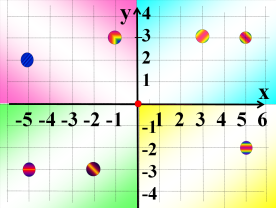
9. Запишіть координати точок, зображених на малюнку

10) Побудуйте точки: А(4;0), В(-2;0), F(-4;0), M(6;0)

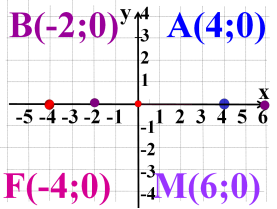
11.    Де розташовані побудовані точки?
12.    Побудуйте точки: A(0;2), B(0;3), F(0;-2), M(0;-4)

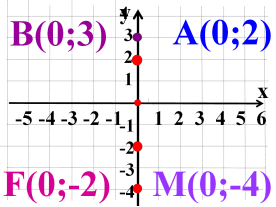
13.    Де розташовані ці точки?
14.    Чи правильно побудована точка? Якщо ні, то вкажіть її місце розташування.

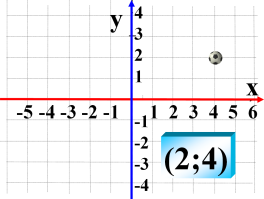
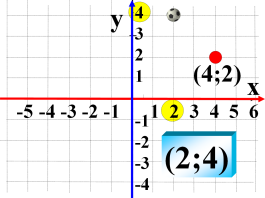
15.    Вкажіть координати точок перетину сторін трикутника з віссю абсцис, з віссю ординат

Підрахуйте кількість балів отриманих за математичний диктант

Кіл-ть правильних відповідей	Кіл-ть отриманих балів
1-6	0
7-12	1
13-18	2
19-24	3
25-30	4

3. Перевірка домашнього завдання

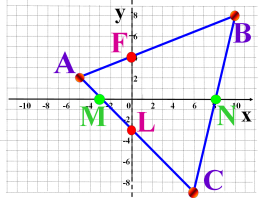
№1334. Вкажіть координати точок E, F, L, M, A.

№1336. Вкажіть ті точки, які розташовані в ІІ та ІІІ координатних чвертях.

Учні отримують по 0,5 бала за кожен правильно розв’язане завдання.

 

 

 

ІІІ. Мотивація

 

Звертаючись один до одного, люди часто говорять: «Залиште свої координати». Для чого? Щоб людину можна було легко знайти. Це може бути: номер вашого телефону, домашня адреса, місце роботи. Суть системи координат полягає в тому, що це правило, за яким визначають положення об’єкта. Системи координат оточують нас усюди. Наприклад, ми купили квиток до кінозалу. Там обов’язково вказані ряд і місце.

Приведіть інші подібні приклади.

Прикладами можуть бути: білет на поїзд, положення географічного об’єкта на карті чи глобусі, визначення місця розташування корабля на ігровому полі в грі «Морський бій», розташування фігур на шаховій дошці, визначення місця знаходження об’єктів льотчиками, моряками, визначення розташування зірок на зоряній карті. (Відповіді супроводжуються показом малюнків).

 

ІV. Оголошення теми та мети уроку

 

V. Місце уроку в темі

 

Цей урок є ключовим уроком в темі.

 

VІ. Очікувані результати

 

Після уроку ви зможете:

• будувати точки за вказаними координатами, при цьому отримувати малюнок;
• визначати необхідні точки та вказувати їх координати;
• розв’язувати завдання з використанням отриманих знань з теми.

 

VІІ. Застосування вивченого матеріалу до розв’язування завдань

 

1. Як знайти периметр та площу прямокутника?
2. Колективне розв’язування задачі.

Дано координати трьох послідовних вершин прямокутника ABCD.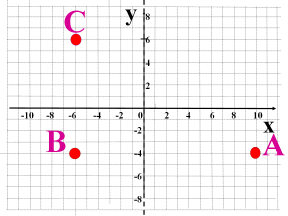

1. Накресліть цей прямокутник.
2. Запишіть координати точки D.
3. Знайдіть периметр і площу прямокутника.
4. Вкажіть координати точок перетину з віссю абсцис, з віссю ординат.
5. Побудуйте діагоналі та запишіть координати точки перетину діагоналей.

Учні мають можливість отримати 1 бал за правильне виконання  одного з пунктів завдання.

3. Самостійна робота.

Учням пропонуються завдання різні за рівнем складності та за формою виконання.

Діти самостійно обирають собі завдання. Кожне завдання дає можливість отримати певну кількість балів. Самостійна робота завершується взаємоперевіркою

Завдання для самостійної роботи.

1. У координатній площині побудуйте точки та назвіть фігуру, вершинами якої є ці точки: P(-2;5), Q(-4;3), R(4;-5), S(6;-3)  [A(1;3), B(-2;-3), C(2;-5), D(5;1)]                                                                                              (1 бал)
2. Запишіть координати точок, зображеного на малюнку сузір’я Цефея [Персея]                                                                                           (1 бал)
3. Побудуйте фігуру за даними точками, послідовно їх з’єднуючи: A: (7;0), (5;-2), (3;-2), (2;-4), (0;4), (-1;-2), (-5;0), (-7;-2), (-8;-1), (-7;1), (-8;3), (-7,4), (-5;2), (-3;2), (0;3), (3;3), (5;2), (7;0)   B:  (-4;-2), (-3;4), (2;4), (3;3).

[(6;1), (3;-3), (1;-4), (-4;4), (-2;-3), (-5;-2), (-5;2), (-3;3), (-6;3), (-3;4), (-5;7), (-3;6), (1;7), (3;5), (-1;2), (1;2), (3;0), (6;1).]                             (2 бали)

4. Обчисліть другу координату точки-зірочки, побудуйте сузір’я Великої Ведмедиці

а) x=5, y=2x-9;

б) x=3, y=x;

в) x=-10+11, y=4;

г) x=-1, y=7x+11;

д) x=-4, y=x+7;

е) x=-5, y=|x|;

є) x=-2, y=2x+10

[Малої Ведмедиці]

a) y=1, x=3y-10;

б) x=-3, y=|x|-3;

в) x=-1, y=2x;

г) x=1, y=-x-2;

д) x=6, y=x-10;

е) x=5, y=-11+x;

є) x=1, y=2-7x;        (2 бали)

 5)           За двома вершинами В та С прямокутника АВС та точкою О – перетину

                         його діагоналей добудуйте прямокутник. Вкажіть координати вершин A

                         і D. Запишіть координати точок перетину сторін прямокутника з віссю

                         абсцис та віссю ординат. Знайдіть периметр та площу прямокутника. 3 бали

         

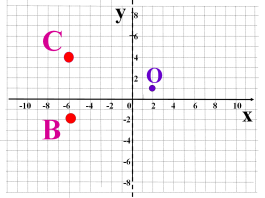
Учні виконують взаємоперевірку та підраховують кількість набраних балів за самостійну роботу.

 

VІІІ. Підсумок уроку

 

1. Підрахуйте кількість балів, отриманих за урок
2. Що нового дізналися?
3. Чи сподобався вам урок?

 

ІХ. Домашнє завдання

 

Повторити п.45, №1342, 1347, 1349*.