Урок математики з теми "Тригонометричні функції"
Дану розробку уроку можна використовувати під час систематизації знань учнів з теми "Тригонометричні функції". Вона містить завдання, розроблені у вигляді гри для оцінювання знань учнів, такі як: "Математичне доміно", "Чи вірете ви, що...?".
Основна мета застосування ділової гри на уроці математики – це розвиток стійкого пізнавального інтересу в учнів до предмету, вироблення критичного ставлення до себе, уміння бачити свої помилки та адекватно ставитися до них.
Тема уроку: Тригонометричні функції
Мета уроку:
навчальна:
- узагальнити знання про графіки тригонометричних функцій та їх властивості; вміння виконувати перетворення графіків функції;
- формувати вміння і навички користуватися тригонометричними формулами додавання для перетворення тригонометричних виразів;
розвиваюча:
- розвивати розумові здібності, здатність до самостійного мислення, пам’ять, увагу;
- розвивати комунікативні здібності учнів, вміння працювати в групах;
виховна:
- виховувати працьовитість, охайність, культуру поведінки та математичної мови, інтерес до вивчення предмету;
- прищеплювати бажання мати якісні знання;
- сприяти розширенню кругозору учнів.
Тип уроку: систематизації та узагальнення знань, урок – гра.
Методи навчання, прийоми: математичний диктант, фронтальне опитування, гра «Чи вірите ви, що…», робота в групах.
Міжпредметні зв’язки: геометрія, література.
Наочність: презентація «Тригонометричні функції», лист самоконтролю, картки – завдання.
Технічні засоби навчання: комп`ютер, інтерактивна дошка, програма Power Point.
Хід уроку
- Організаційний момент.
1.1. Привітання учнів.
1.2. Перевірка готовності до заняття учнів, обладнання.
1.3. Розміщення учнів по групах.
- Повідомлення теми заняття, формування мети та основних завдань заняття. (слайд 1-3)
Слово викладача
Епіграф до заняття
ЩАСТЯ ДАЄТЬСЯ ТОМУ, ХТО БАГАТО ПРАЦЮЄ
ЛЕОНАРДО ДА ВІНЧІ
Працюємо по групах. Давайте визначимо капітанів у кожній з груп.
Команди: (Слайд 4)
- Синус
- Косинус
- Тангенс
- Котангенс
Протягом заняття заповнюємо лист самооцінки, в якому вказано кількість балів, які можна отримати за кожне завдання та вказуєте набрані бали.
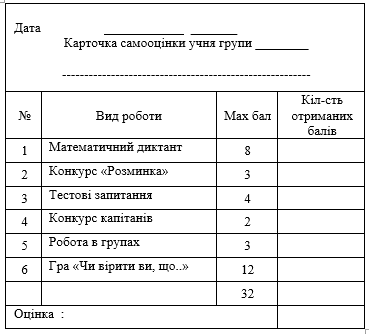
Норми оцінювання:
- 31-32 бали - оцінка «12»;
- 28-30 - оцінка «11»;
- 25-27 – оцінка «10»;
- 22-24 - оцінка «9»;
- 19-21 - оцінка «8»;
- 17-18 - оцінка «7»;
- 13-16 – оцінка «6»;
- 10-12 – оцінка «5»;
- 7-9 – оцінка «4»;
- 5-6 – оцінка «3»;
- 3-4 - оцінка «2»;
- 1-2 - оцінка «1».
Розпочнемо з першого завдання.
- Привітання гостей (математичний диктант). Вам необхідно відповісти на питання та вписати в таблицю перші літери відповідей. (Слайд 5)
- Синусоїда, косинусоїда, тангенсоїда, котангенсоїда – назви …
(графіків)
- Вісь Оу – це вісь …
(ординат)
- Яка функція відсутня:
(синус)
y = cosx
y = tgx
y = ctgx
4.Синус, косинус, тангенс, котангенс – це … функції
(тригонометричні)
5. Я
6. Значення, яке приймає залежна змінна…
(множина)
7. Міра виміру кута…
(радіан)
8. Пряма, до якої крива при віддаленні в нескінченність наближається як завгодно близько, але не перетинає її….
(асимптота)
9. Частина кола …
(дуга)
10. І
Перевірка правильності виконання завдання(Слайд 6)
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
|
Г |
о |
с |
т |
я |
м |
р |
а |
д |
і |
- Розминка Кожна команда отримує по 3 питання. Правильна відповідь на запитання оцінюється в 1 бал. (Слайд 7)
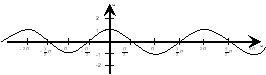
Завдання для 1 команди
- Вкажіть графік якої функції зображено на малюнку?
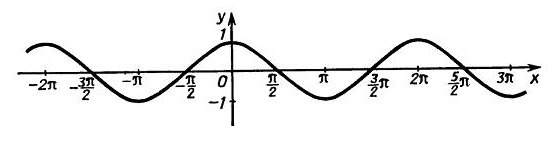
(косинус).
- Симетрія графіка парної функції.
(відносно осі ОУ).
- y = 0,5sinx. Яке перетворення необхідно виконати з графіком даної функції?
(виконати стиск відносно осі oy)
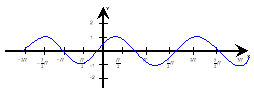
Завдання для 2 команди
- Вкажіть графік якої функції зображено на малюнку?
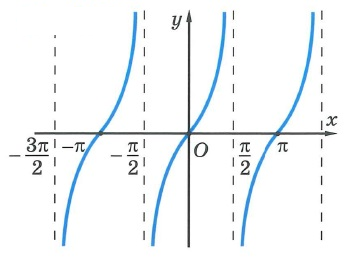
(тангенс).
- Період функції y = sinx?
(Т = 2π).
- y = sinx – парна чи непарна функція?
( непарна).
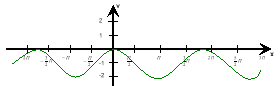
Завдання для 3 команди
- Вкажіть графік якої функції зображено на малюнку?
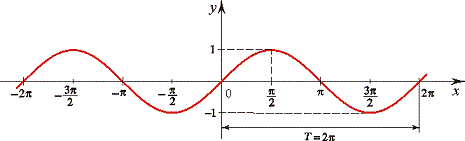
(синус).
- Період функції y = cosx?
(Т = 2π).
- y = tgx – парна чи не парна функція?
(не парна).
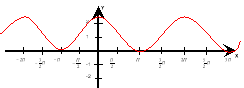
Завдання для 4 команди
- Вкажіть графік якої функції зображено на малюнку?
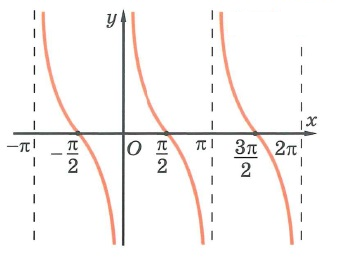
(котангенс).
- Область визначення функції y = sinx, y = cosx.
(R)
- Множина значень функції y = sinx, y = cosx.
([-1;1])
4.Тестові завдання (На бланку відповідей відмітити правильну відповідь)
Питання 1. На якому з малюнків зображено графік функції y = sin2x,
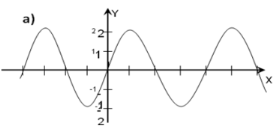

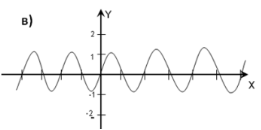
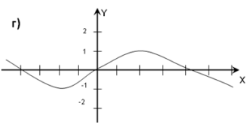
Питання 2. Який із малюнків відповідає графіку функції y = cos(x+1)?
|
А |
Б |
|
В |
Г |
Питання 3. Для кожної із названих функцій вказати її область визначення
|
Функція |
Область визначення |
|||
|
R |
R |
|
|
|
|
Cosx |
|
|
|
|
|
Sinx |
|
|
|
|
|
Ctgx |
|
|
|
|
|
Tgx |
|
|
|
|
Питання 4. Установіть відповідність між функціями та геометричними перетвореннями графіка функції y=sinх
- y=sinx+4
- y=sin(x+4)
- y=sin (x-4)
- y=4sinx
A Графік функції y=sinx перенесли паралельно осі Оу на чотири одиниці ліворуч
Б Графік функції y=sinx перенесли паралельно осі Ох на чотири одиниці вгору
В Графік функції y=sinx стиснули до осі Оy у чотири рази
Г Графік функції y=sinx розтягнули від осі Ох у чотири рази
Д Графік функції y=sinx перенесли паралельно на чотири одиниці праворуч
Перевірка правильності відповідей (Слайд 8-11)
5. Конкурс капітанів (Слайд 12)
Капітан кожної команди виходить до дошки і розв’язує завдання.
Скласти алгоритм побудови графіка функції.
Завдання для команди «Синус» y = 2cos(x + ![]() ) – 1
) – 1
Завдання для команди «Косинус» ![]()
Завдання для команди «Тангенс» ![]()
Завдання для команди «Котангенс» ![]()
Поки капітани працюють, кожна команда отримує своє завдання. Користуючись графіком функції y=sinx, необхідно побудувати графік функції:
Для команди «Синус» - y= sin(x-![]()
Для команди «Косинус» - y=sin(x+![]()
Для команди «Тангенс» - y=sinx+1
Для команди «Котангенс» - y=sinx-1,5
Правильність виконання завдання (Слайд 13)
6. Гра «Чи вірите ви, що…?» (Слайд 14-15)
Учаснику команди будуть ставитись запитання, в залежності від відповіді -«так» або «ні» - буде формуватись вислів. Частини вислову учасники збирають у себе на парті.
1. Найбільше значення функції у=sinx дорівнює 1
2. Найменше значення функції у=cosx дорівнює -1
3. Найбільше табличне значення функції у=tgx дорівнює ![]()
4. Найбільшого табличного значення функції у= сtgx не існує.
5.Чи правильно вказана формула ![]() ?
?
6. Чи вірно вказана формула ![]() ??
??
7. Графік функції у= tgx проходить через початок координат?
8. Функція у=sinx може бути або парною, або не парною залежно від значення х
9. Період тригонометричних функцій дорівнює 2π
10. З усіх тригонометричних функцій тільки функція у=cosx парна.
11. tg![]() =1
=1
12. ![]() =1
=1
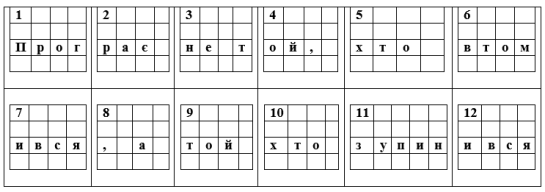 Правильне формулювання вислову: (Слайд 16)
Правильне формулювання вислову: (Слайд 16)
- Підведення підсумків.
Викладач:
Всі команди – молодці
Працювали від душі
Знаємо тепер ми і синус і косинус і тангенс і котангенс
І як графік будувати і рівняння як рішать
А просто все це треба добре знать
І ніколи не забувати
Урок успішно пройшов
А це значить, що у нас
Все добре в даний час.
Остаточно перевірити свої листки самооцінки, поставити кількість балів за останнє завдання і віддати їх капітану своєї групи. Капітани зберіть листки і віддавайте мені на перевірку. На наступному уроці обов’язково оголошу.
-
Домашнє завдання: Підручник В.Г.Бевз, Г.П.Бевз «Математика 10», розділ II, повторити основні формули тригонометрії, підготуватися до контрольної роботи. Побудувати графік функції: y= -tg (x+
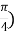 .
.


про публікацію авторської розробки
Додати розробку