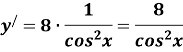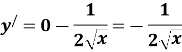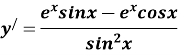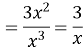Методична розробка уроку з математики на тему: «Похідна складеної функції»

БЕРДЯНСЬКИЙ ЕКОНОМІКО-ГУМАНІТАРНИЙ КОЛЕДЖ

БЕРДЯНСЬКОГО ДЕРЖАВНОГО ПЕДАГОГІЧНОГО УНІВЕРСИТЕТУ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Методична розробка

відкритого уроку з математики

 

Тема: «Похідна складеної функції»

 

 

 

Підготував викладач математики

Костюкович Вікторія Володимирівна

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема: Похідна складеної функції

Мета  уроку:

•    навчальна – продовжувати формувати вміння, навички знаходження похідних елементарних функцій за таблицею та правилами, сформувати поняття «складена функція», формувати вміння розрізняти складені функції від елементарних, вміння вказувати зовнішню та внутрішню функції у складеній, ознайомити з алгоритмом знаходження похідної складеної функції, формувати вміння знаходити похідні складених функцій за алгоритмом;
•    розвивальна – розвивати логічне, аналітичне, критичне мислення, пам’ять, вміння концентрувати увагу, правильне математичне мовлення; формувати навички самоконтролю.
•    виховна – виховувати активність, цілеспрямованість, любов до навчання, повагу один до одного.

Типу року: засвоєння нових знань.

Обладнання: інтелект-карта «Похідна» (формат А-1); таблиці: «Похідні елементарних функцій», «Правила знаходження похідних», «Утворення складеної функції (Рис.3)», «Тренувальна таблиця (Таблиця 3)»; роздатковий матеріал: алгоритм знаходження похідної складеної функції, картки для фронтального розв’язування вправ, картки для самостійної роботи, картки-розв`язки до завдань самостійної роботи; підручники (Бевз Г.П. Математика: 11 кл.: підруч. для загальноосвіт. навч. закл.: рівень стандарту / Г.П.Бевз, В.Г.Бевз. – К.: Генеза, 2011); матрьошки.

Хід уроку

I.     Організаційний момент. Перевірка готовності учнів до уроку, відмітка присутніх (відсутніх), налаштування на роботу.

II.     Перевірка домашнього завдання. Шляхом з`ясування труднощів (викладач відповідає на питання учнів, які виникли в них під час розв`язування домашніх прикладів, збирає зошити з д/з на перевірку, роздає перевірені).

III.     Формулювання теми, мети, задач уроку; мотивація. Актуалізація опорних знань.

3.1.       Робота з інтелект-картою. За інтелект-картою «Похідна» (Рис.1) учень розказує що вже вивчили з теми «Похідна та її застосування» (які знання одержали, вміння та навички сформували). Викладач повідомляє з чим познайомимось сьогодні і що залишиться освоїти на наступних уроках.

Сьогодні необхідно з`ясувати, які функції називаються складеними, як їх відрізняти від елементарних та яким чином (за яким алгоритмом) знаходити похідні складених функцій.

3.2.       Виконання завдань

(Формування вміння чітко встановлювати що являє собою функція, а також вміння знаходити похідні елементарних функцій за таблицею похідних та правилами знаходження похідних)

1)       Дайте відповіді на запитання: «Що представляє собою кожна з поданих функцій?» (Функції подані в першому стовпчику таблиці 1, викладач записує їх на дошці перед уроком)

(Відповіді: 1) елементарну функцію; 2) добуток постійного множника на елементарну функцію; 3) різницю двох елементарних функцій; 4) добуток двох елементарних функцій; 5) частку двох елементарних функцій.)

 

Рис.1. Інтелект-карта «Похідна»

 

2)       Знайдіть похідні даних функцій (Учні по одному виходять до дошки, записують похідні).

Таблиця 1

Функція	Похідна функції
1.     1.
2.
2.     3.
3.     4.
4.     5.

 

4. Вивчення нового матеріалу
   1.   Завдання на розвиток вміння порівнювати та критично сприймати інформацію, розуміння того, що функція і аргумент можуть позначатися різними літерами латинського алфавіту; введення нового запису похідної (зі вказівкою аргументу).

Робота за таблицею 2 (Таблицю викладач пише заздалегідь на додатковій дошці або на правому крилі основної дошки)

Викладач. Чи різні перед вами функції? Ні, функція одна, різні її позначення. Функція – це залежність між двома змінними. Змінні можна позначати будь-якими буквами латинського алфавіту. Які букви використані для позначення аргументу в 1-5 функціях? (x, t, g, d, u) А для позначення функції? (у, s, f, w) За якою формулою треба шукати похідну цієї функції?()

Похідну функції можна позначати по-різному: , , . В останніх двох записах вказано аргумент!

Далі викладач коментує І рядок таблиці 2, учні - інші рядки (викладач поступово, за відповідями учнів, доповнює правий стовпчик).

Таблиця 2

1	- у є функцією, аргументом якої є змінна х ()		Похідною функції у по аргументу х буде
2	()
3	()
4	()
5	()

 

2.   Введення поняття складеної функції.

Рис.2.Матрьошки

Рис.3. Утворення складеної функції

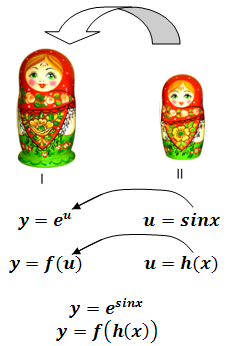
Викладач. Пригадаємо улюблені дитячі іграшки «Матрьошки» (Рис.2).

Поставимо у відповідність матрьошкам І, ІІ функції:   (),   () (Рис.3).

Помістимо матрьошки одна в одну.

З функціями зробимо те саме: функцію ІІ «помістимо» у функцію І, одержимо:

   [ ].

Ця функція буде складеною з двох елементарних функцій:

зовнішньої: 

внутрішньої:  .

 В математиці досить часто зустрічаються складені функції. Ви повинні навчитися відрізняти їх від елементарних.

 Завдання. Порівняйте функції у І-ІІІ стовпчиках тренувальної таблиці (Таблиця 3) та встановіть чи будуть складеними функції у ІІІ стовпчику (відповідь поясніть).

 

 Висновок

 Складена функція – функція від функції, вона схожа на одну з елементарних, у якої замість аргумента х стоїть деяка функція (вираз) від х.

 

Таблиця 3

Елементарні функції	Складені функції	Чи буде складеною функція?
;
;
;
;

 

3.       Виконання вправ усно (фронтально):

 №311 – утворіть складену функцію з двох елементарних (складіть матрьошку), звертаючи увагу на те, яка з них буде зовнішньою, яка внутрішньою.

 №312 – розкладіть складену функцію на дві елементарні, вказавши яка з них зовнішня, яка внутрішня (розберіть матрьошку).

4.       Ключове питання: Як знаходити похідні складених функцій?

 На нього відповість теорема (Підручник с.73.):

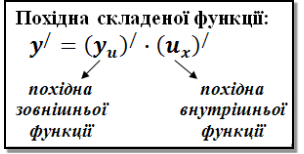
 Нехай дано функцію , де . Якщо в якійсь точці х існує похідна та у відповідній точці існує похідна , то існує також похідна .

Рис.4. Похідна складеної функції

 Учні виписують в зошит тільки останню рівність теореми, обводячи її в рамку як формулу та вказуючи зовнішню і внутрішню функції (Рис.4)

 Правило знаходження похідної складеної функції: похідна складеної функції дорівнює добутку похідної зовнішньої функції по проміжному аргументу на похідну внутрішньої функції по аргументу х.

 Викладач. Доведення теореми складне, воно розглядається у вищій математиці. Наша з вами задача навчитись застосовувати її для знаходження похідних складених функцій.

 Приклад. Знайдіть похідну функції:   .

 Алгоритм знаходження похідної складеної функції (Учні зачитують з карток пункти алгоритму, викладач демонструє кожен пункт на прикладі):

 1. Впевнитись, що дана функція є складеною

(Функція є складеною, бо являє собою функцію від функції; вона схожа на елементарну функцію тільки замість аргументу х стоїть функція ).

 2. Розібрати складену функцію на елементарні, встановивши зовнішню функцію від проміжного аргументу та внутрішню функцію від аргументу х

(зовнішня функція: ; внутрішня функція: ).

 3. За теоремою про похідну складеної функції знайти добуток похідної зовнішньої функції по проміжному аргументу та похідної внутрішньої функції по аргументу х. В кінці замінити проміжний аргумент виразом з аргументом х

().

5. Первинне закріплення матеріалу

Фронтальне розв`язування вправ (Формуємо логічність, послідовність мислення, вміння знаходити похідні складених функцій за алгоритмом).

 Учні відповідають з місць, викладач записує на дошці (у вигляді таблиці). Учні роблять записи на картках під номером 1 (Таблиця 4).

 Заповнюється спочатку ІІІ рядок таблиці (…, … для всіх функцій), потім ІV (…).

Таблиця 4

Картка №1
Складена функція
Вкажіть зовнішню та внутрішню функції
Знайдіть	Формула:	Формула:	Формула:

 

6. Формування вмінь, навичок.

6.1.Робота в парах. Учні виконують завдання на картках №2 (Таблиця 6), допомагаючи один одному.

Таблиця 6

Картка №2
Складена функція
Вкажіть зовнішню та внутрішню   функції
Знайдіть	Формула:	Формула:	Формула:

 

 

6.2.Самоперевірка роботи за карткою-розв`язком (Таблиця 7).

Таблиця 7

Картка-розв’язок

 

Додатково (в зошитах): №318 (а), 322(г), 324(в) – 12 балів.

 

7.       Домашнє завдання

За підручником:

№315(а,в), 316(а,в) –з двох елементарних функцій утворіть складену (складіть матрьошку) №316(а,в) – для даної функції вкажіть зовнішню та внутрішню функції (розберіть матрьошку)	По 1 балу за приклад	Всього 6 балів
№318(а), 323(а), 327(б) - зайдіть похідні складених функцій	По 2 бали за приклад	Всього 6 балів
Всього 9 прикладів		Разом 12 балів

Додаткове завдання:

Утворіть складену функцію з трьох елементарних (Складіть три матрьошки одна в одну) та знайдіть її похідну за формулою:

8.       Підсумок уроку

Бесіда за питаннями: Чим ми займались сьогодні на уроці? Що повторили? Що нового дізналися? Хто зрозумів що таке складена функція? Сформулюйте правило знаходження похідної складеної функції. Якого алгоритму слід дотримуватись шукаючи похідну складеної функції?

 Оцінювання роботи учнів на уроці.