Урок " Методи і прийоми розв"язування логарифмічних рівнянь"

Управління освіти Шосткинської міської ради Сумської області

Комунальна організація (установа, заклад) «Шосткинська загальноосвітня школа I-III ступенів №4 Шосткинської міської ради Сумської області»

 

 

 

 

Розробка уроку

алгебри і початків аналізу в 11 класі

Методи і прийоми розв’язування

логарифмічних рівнянь

 

 

 

 

 

Підготувала

вчитель математики

Аврамкіна В. І.

 

 

 

2019 рік

Тема уроку «Методи і прийоми розв’язування

логарифмічних рівнянь»

Мета уроку:

• навчальна: систематизувати та узагальнити знання учнів про логарифми та їх властивості; формувати вміння і навички розв’язувати логарифмічні рівняння, користуючись означенням та властивостями логарифма;
• розвивальна: вдосконалювати навички застосовувати властивості логарифмів під час розв’язування рівнянь; розвивати розумові здібності, здатність до самостійного мислення;
• виховна: виховувати працьовитість, культуру математичних записів та інтерес до вивчення предмета.

Тип уроку: узагальнення й систематизація знань, умінь і навичок.

Обладнання: мультимедійний проектор, картки із завданнями, тестові завдання, картки самооцінки.

Форми роботи: індивідуальна, колективна, усна, тестова перевірка знань, самостійна робота.

Хід уроку

І. Організаційний етап

 Привітання. Перевірка готовості учнів до уроку

ІІ. Перевірка домашнього завдання

Вправа «Знайди помилку товариша»

Учні обмінюються зошитами і перевіряють виконання домашніх вправ сусідом по парті за розв’язаннями на слайді

 Учні оцінюють одне одного:

• правильно виконане завдання – 3 бали;
• 1 – 2 помилки – 2 бали;
• 3 помилки – 1 бал;
• більше помилок – 0 балів.

 

Перевірка домашнього завдання

Знайди помилку товариша

1. Розв’яжіть рівняння

 log₂(x-2) = log₂(x²-x-17)

Розв’язання

Подане рівняння рівносильне системі:

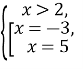
     x = 5.

Відповідь: 5.

2. Розв’яжіть рівняння

log₃( + 1) + log₃( + 3) = 1

Розв’язання

ОДЗ:   > 1.

log₃( + 1)( + 3) = 1,  ( + 1)( + 3) = 3,  ² +4 = 0,

звідки = 0 або = 4.

Число не належить до ОДЗ рівняння.

Відповідь: 0.

3. Розв’яжіть рівняння

lg² = 4 – 3lg

Розв’язання

lg² + 3lg – 4 = 0

Введемо заміну: lg = y, тоді y² + 3y – 4 = 0, звідки y = 1 або y = – 4.

Маємо:    

Відповідь: 0,0001; 10.

 

 

 

ІІІ. Мотивація навчальної діяльності.                                                                  Повідомлення теми, мети і завдань уроку.                                                             Учитель. Я впевнена, що цей урок мине цікаво і корисно для всіх.

Алгебру називають теорією розв’язування рівнянь і вивчення властивостей функцій. Сьогодні ми вдосконалюватимемо вміння розв’язувати логарифмічні рівняння. Для успішного розв’язування вправ на уроці ви повинні вміти:

• правильно визначати тип логарифмічних рівнянь;
• застосовувати властивості логарифмів;
• застосовувати властивості логарифмічної функції до розв’язування рівнянь.

IV. Відтворення і корегування опорних знань, навичок і вмінь. 

Хвилинка ерудита

Фронтальне опитування

1) Що називають логарифмом числа b за основою a?

2) Як правильно прочитати запис log₅ 20 ?

3) Що означають записи lg b, ln b ?

4) Чому дорівнює логарифм числа а за основою а ?

5) Чому дорівнює логарифм числа 1 за основою а ?

6) Чому дорівнює логарифм добутку додатніх чисел ?

7) Чому дорівнює логарифм частки додатніх чисел ?

8) Чому дорівнює логарифм степеня додатного числа ?

9) Чи існує логарифм від’ємного числа ?

Усні вправи

log₃

log₅

log_x 15

log₈ 2

lg 8 + lg 125

lg 0,001

lg 5 – 1

 

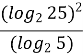
Письмове виконання вправ

Учні біля дошки виконують завдання з повним обгрунтуванням.

Знайти значення логарифма, застосовуючи властивості логарифма:

1) log₂ 24 – log₂ 3

2) log₅ 11 – log₅ 22 + log₅ 10

3) log₂ 63 – log₂ 7 – log₂ 36

4) log₅ - 2log₅  + log₅

5) log₃ 8 – 2log₃ 2 + log₃ 

Відповіді:

1) 3	4) -1
2) 1	5) 2
3) -2

 

 

 

V.  Узагальнення і систематизація знань з даної теми

Вправа «Знайди друга» (Індивідуальна робота)

Оцінювання: 6 завдань – 3 бали; 5 завдань – 2 бали; 4 завдання -1 бал; 0-3 завдання – 0 балів.

Обчисліть і вкажіть правильну відповідь:

№	Завдання	Варіанти відповідей
1	2 8	3
2	4 16	0
3	4	1
4	5 5	4
5	3 1	-2
6	5 625	2

Відповіді:

1) 3	4) 1
2) 2	5) 0
3) -2	6) 4

Математичний диктант

Обчисліть:

1) 2 16	7)
2) 100	8)
3) 8 8	9) 3 8 * 2 3
4) 3 1	10) 3 8 – 3 2
5)	11) ОДЗ функції: 2(1-x)
6)	12) Чи має зміст вираз: -x(x-1)

Наприкінці відбувається взаємоперевірка.

12-10 виконаних завдань – 3 бали;

9-7 виконаних завдань – 2 бали;

6-4 виконаних завдань – 1 бал;

3-0 виконаних завдань – 0 балів.

 

VI. Застосування узагальнених знань умінь і навичок учнів

Учням пропонується слайд з асоціативною схемою, за якою вони відтворюють види та способи розв’язання логарифмічних рівнянь:

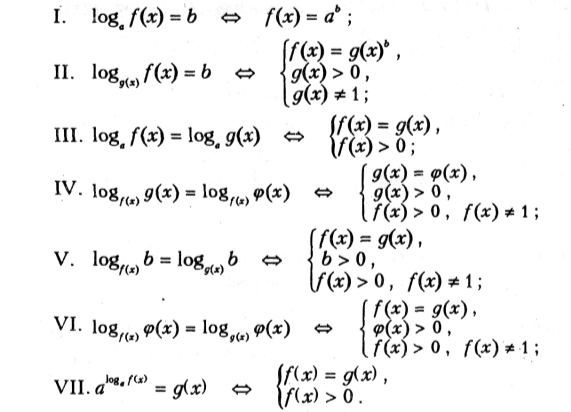Основні типи логарифмічних рівнянь розв’язуються за такими схемами (a > 0, a ≠ 1) :

 

 

 

 

 

 

 

 

.

 

При розв’язуванні рівнянь мішаного типу, які містять показникові та логарифмічні функції, застосовують логарифмування або основну логарифмічну тотожність.

При потенціюванні можлива як поява сторонніх розв’язків внаслідок розширення ОДЗ, так і їх втрата при звуженні ОДЗ.

Письмове розв’язування логарифмічних рівнянь

Спочатку учням пропонується висунути ідею щодо розв’язування кожного рівняння, далі обговорюємо її.

Потім демонструємо слайди з розв’язанням рівнянь, звертаємо увагу учнів на «контрольні» моменти розв’язування. Далі пропонуємо учням розв’язати ці рівняння вдома.

Розв’яжіть рівняння:

1) lg(x² – 2x) = lg(2x + 12)

2) log₂(x + 13) = 2log₂(x + 1)

3) lg(x + 4) + lg(2x + 3) = lg(1 - 2x)

4) lg²100x – 5lgx = 6

5) x^lgx-1 = 100

Розв’язування з коментарями:

№	Рівняння	Коментарі до розв’язування
1	lg(x2 – 2x) = lg(2x + 12)	Рівняння рівносильне системі:   Відповідь: -2; 6.
2	log2(x + 13) = 2log2(x + 1)	ОДЗ рівняння знайдено із системи нерівностей: Звідки x > -1. Знаходження ОДЗ є необхідною умовою, оскільки під час перетворення 2log2(x+1) = log2(x+1)2 Відбувається розширення ОДЗ (можна дістати корені, що не належать до ОДЗ). Відповідь: 3.
3	lg(x + 4) + lg(2x + 3) = lg(1 - 2x)	ОДЗ рівняння знайдено із системи нерівностей: звідки х Є (-1,5; 0,5). Увага! Під час додавання логарифмів відбувається розширення ОДЗ. lg((x+4)(2x+3)) = lg(1-2x). Відповідь: -1.
4	lg2100x – 5lgx = 6	ОДЗ: х>0 Подамо рівняння у вигляді: (lg100+lgx)2 – 5lgx – 6 = 0. Нехай lgx = y, тоді рівняння набуває вигляду: y2-y-2 = 0. Відповідь: 0,1; 100.
5	xlgx-1 = 100	ОДЗ: х>0 Прологарифмуємо обидві частини рівняння за основою 10, маємо: lgx(lgx-1) = 2. Це рівняння заміною зведемо до квадратного. Відповідь: 0,1; 100.

 

 

VII. Контроль і самоконтроль знань, умінь і навичок

Учні виконують тестові завдання, запропоновані їм за допомогою мультимедійної дошки.

Оцінювання: за правильно виконані 9-10 завдань – 3 бали, 7-8 завдань – 2 бали, 5-6 завдань – 1 бал, 0-4 завдань – 0 балів.

1) Обчислити

А	Б	В	Г
2	1		-1

2) Чому дорівнює х, якщо log_0,4x = log_0,48 ?

А	Б	В	Г
8	0,4	-8	1

3) Розв’язати рівняння log₈x = 2

А	Б	В	Г
26	-64	2	64

4) Чому дорівнює значення виразу log₆9 + log₆4 ?

А	Б	В	Г
log613	12	2	6

5) Обчислити значення виразу

А	Б	В	Г
4	10	25	8

6) Розв’язати рівняння log_0,2(2x-3) = -1

А	Б	В	Г
2,5	4	1	1,4

7) Обчислити значення виразу log₂24 – log₂3

А	Б	В	Г
log221	4	3	2

8) Обчислити значення виразу log₃

А	Б	В	Г
3	-3		9

9) Коренем, якого рівняння є число 16?

А	Б	В	Г
log8х=2	log2х=8	log4х=2	log4х=4

10) 7) Обчислити значення виразу log₂

А	Б	В	Г
2	3	-3

 

VIII. Підсумки уроку. Рефлексія

Учитель: На уроці ви добре попрацювали, продемонстрували знання, активність, добре мислили.

Тепер давайте оцінимо вашу роботу на уроці.

• Що було вдалим на уроці?
• Чого навчилися на уроці?

 

IX. Домашнє завдання

Пропонуємо учням слайд із рівняннями (див. етап уроку «Письмове розв’язування логарифмічних рівнянь»)

Додаток

Картка самооцінки
Прізвище, ім’я:
1	Домашнє завдання (взаємоперевірка)
2	Вправа «Знайди друга» (Індивідуальна робота)
3	Математичний диктант
4	Тестові завдання
5	Активність на уроці, усне опитування
	Оцінка за урок (кількість балів)