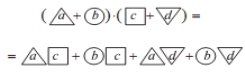Урок "Множення двох многочленів"

Тема: МНОЖЕННЯ ДВОХ МНОГОЧЛЕНІВ

Мета: сформувати в учнів знання алгоритму множення двох многочленів як наслідку з алгоритму множення одночлена на многочлен; виробити вміння перетворювати добуток двох многочленів у многочлен стандартного вигляду за названим алгоритмом, формувати  поняття: компетенція, компетентний, вміння узагальнювати, робити висновки; розвивати логічне мислення та мовлення учнів; розвивати комунікативні навички учнів; виховувати розуміння значимості алгебри як науки серед інших наук. ( формувати процедурну, логічну, загальнокультурну компетентність).

Тип уроку: засвоєння знань.

Хід уроку

 

І. Перевірка домашнього завдання

Зібрати зошити учнів на перевірку. З’ясувати питання, які виникли під час домашнього завдання

Вчитель. Я рада вітати вас на уроці та хочу дізнатися з яким же настроєм  ви прийшли на урок. Настрій добрий, розпочинаємо працювати.

Здобувати знання – хоробрість.

 Примножувати їх – мудрість.

А вміло застосовувати – велике мистецтво!

То ж, поєднавши хоробрість з мудрістю, ми спробуємо на уроці досягти великого мистецтва

ІІ. Актуалізація опорних знань

1. Що таке многочлен?

2. У чому полягає зведення многочленів до стандартного вигляду?

3. Що є степенем многочлена?

4. Які тотожні перетворення многочленів вам відомі?

5. Зведіть подібні доданки многочлена.

4. Чому дорівнює добуток одночлена на многочлен? Яка властивість арифметичних дій при цьому використовується?

5. Які дії можна ще виконувати з многочленом?

ІІІ. Мотивація навчальної діяльності. Оголошення теми і мети уроку

Вчитель: Отже, ще можна множити, ділити та підносити до степеня многочлени. І сьогодні на уроці ми продовжимо розглядати питання, які стосуються дій з многочленами. Тема нашого уроку: «Множення двох многочленів». Мета наша сьогодні  з’ясувати, як множить два многочлени, ми працюватимемо над формуванням навичок множення многочлена на многочлен, розвиватимемо  вміння висловлювати свої думки, математично грамотно їх аргументувати, виховуватимемо любов до математики, прагнення до пізнання незвіданого. Працюватимемо над тим, щоб ви були компетентними в даних питаннях.

А що означає, на вашу думку, бути компетентним?

Компетентний – (лат. competens (competentis) – належний, спроможний) – знаючий, тямущий, обізнаний, досвідчений у деякій предметній області; який може за своїми знаннями або повноваженнями щось здійснювати, або приймати рішення, або судити про щось.

Мистецтво алгебри — наукове мистецтво.

Досконалість цього мистецтва полягає

 в знанні методів вивчення,

за допомогою яких можна осягнути

 спосіб визначення невідомих,

як числових, так і геометричних                                                                                                                                          О. Хайям

IV. Створення проблемної ситуації

Задача. Знайти площу прямокутника, якщо відомі частини його сторін.

В ході розв’язання задачі, учні доходять висновку   , , , , — це не тільки числа, але й вирази.

V. Засвоєння знань

Множення двох многочленів
У словесній формі Щоб помножити многочлен на многочлен, треба кожний член першого многочлена помножити на кожний член другого на многочлен й утворені добутки додати.	У вигляді тотожності
Приклади: 1) ; 2) . Зауваження: 1) у результаті множення двох многочленів утворюється многочлен; 2) многочлен — добуток, зводимо до стандартного вигляду(якщо це можливо)

 

VІ. Засвоєння вмінь

Оскільки алгоритм, сформульований на уроці, є зовсім новим для учнів, вироблення вмінь його застосовувати починаємо з найпростіших вправ, в яких знаходимо добуток лінійних виразів різного типу. При цьому, у разі необхідності, головне — детальний покроковий запис виразів згідно з вивченим алгоритмом і обґрунтованими усними міркуваннями, наприклад:

.

При цьому нагадуємо учням про культуру запису (буквені множники у складі членів многочлена записуємо в алфавітному порядку).

Якщо учні засвоюють цей вид роботи, можна переходити до розв’язування завдань, в яких, окрім вказаного алгоритму, обережно вводяться інші, відомі учням перетворення (але і в цих завданнях не слід згортати записи, бо головна мета — вироблення вмінь правильного застосування алгоритму множення двох многочленів).

Виконання письмових вправ

1. Виконайте множення:

1) ; 2) ; 3) ; 4) ;

5) ; 6) .

2. Спростіть вираз:

1) ; 2) ; 3) ; 4) ;  5)

3. Запишіть у вигляді многочлена вираз:

1) ; 2) ;    3)

4. Подайте у вигляді многочлена вираз:

1) ; 2) ;  3) .

5. Розкрийте дужки:

1) ; 2) .

6. Робота в групах. Створіть правильні тотожності:

 

 

 

 

 

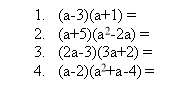
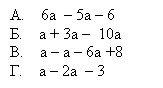
6. Подайте у вигляді многочлена:

1) ;

7. Робота в парах. Спростити вираз:

 ;

VІI. Підсумок уроку  Бліцтест

1. Яка з рівностей правильна? Чому?

     А) ;            Б) ;

     В) ;     Г) .

2.  В якому з виразів допущена помилка?

     А)  (р + с)(в + к) = рв +рк + св + ск;           Б)   (р + с)(п – к) = рп  –  рк + сп  –  ск;

     В)  (р –  с)(п – к) = рп  –  рк + сп  –  ск;   Г)  (р –  с)(п – к) = рп  –  рк  –  сп  +  ск

3. Який з виразів є добутком многочленів та ?

А) ;    Б) ;   В) ;   Г) .

4. Який з виразів тотожно рівний виразу (х + 1)(х – 1)?

А)   х² – 1; Б) х² –  х + х; В) х² – х – 1; Г)  х²  + 1

     Відповівши на запитання тесту, учні відкривають портрет українського вченого математика, академіка  Михайла Пилиповича  Кравчука

  Вчитель:  Кожна людина, яка поважає себе, повинна знати історію рідного краю, та знати людей, якими пишається її народ. Одним із яскравих представників наукової спадщини нашої країни є Михайло Пилипович Кравчук.

     Народився майбутній вчений 30 вересня 1892 р. в селі Човницях на Волині

     1901 р. він разом з батьками перебирається до Луцька, де в 1910 р. закінчує з золотою медаллю гімназію.

Цього року він вступає на фізико- математичний факультет Університету Святого Володимира в Києві.

     Одна за одною з'являються друковані праці М. Кравчука. Ряд глибоких результатів з теорії білінійних форм та лінійних перетворень завершується докторською дисертацією «Про квадратичні форми та лінійні перетворення», яку вчений блискуче захищає 14 грудня 1924 р. Це був перший в УРСР захист докторської дисертації.

     1925 року М. Кравчукові було присвоєно звання професора.  У 1929 році кандидатуру Кравчука висувають у дійсні члени Всеукраїнської академії наук. Він стає наймолодшим академіком України у віці 37 років.

Михайло Кравчук — автор понад 180 наукових робіт з різних галузей математики. Він  одержав фундаментальні результати в теорії ймовірностей,  із теорії функцій дійсної та комплексної змінних, теорії рівнянь, теорії імовірностей та математичної статистики.

   Його наукові результати дістали міжнародне визнання. Серед них і перший проект комп'ютера.

9 березня у засланні видатний вчений померає. Його було реабілітовано лише у 1957 році

    Лише перед 75-річчям від дня народження вченого (1967) почали з'являтися про нього публікації

 2002 року ім'я М. Кравчука внесено ЮНЕСКО до переліку найвидатніших людей світу.

   У 2003 році на території Політехнічного інституту в Києві, вперше в Україні, відкрито пам'ятник всесвітньовідомому математикові Михайлові Кравчуку.

Видано три об'ємні книги М. Кравчука

20 вересня 2012 р. Національний банк України увів в обіг пам'ятну монету номіналом 2 гривні, присвячену М. П. Кравчуку.

    Академік Михайло Кравчук свою різнобічну наукову діяльність розглядав як справу патріотичну, як справу громадянську. Його крилатою фразою були слова  «Моя любов — Україна і математика» .

   Любіть і ви Україну, бо це ваша Батьківщина, і любіть математику, бо вона цариця всіх наук.

 

VІII.  Рефлексія: Інтерактивна вправа “Незакінчене речення”:

Під час проведення уроку мені сподобалося ...

Найскладнішим для мене було ...

Я з’ясував ...

Я добре виконав ...

Я оцінюю свою роботу на уроці ...

 

ІХ. Домашнє завдання

§ 18 – вивчити правило множення многочлена на многочлен, №466, 467, 468

 

№ 2 Випереджальне. Використовуючи повторене означення, подайте у вигляді добутку вирази:

а) ; б) ; в) ; г) ; д) ; е) .

Чи можна перетворити ці добутки у многочлен стандартного вигляду? Чому? Як?