Урок на тему "Графік функції" Презентація
Про матеріал
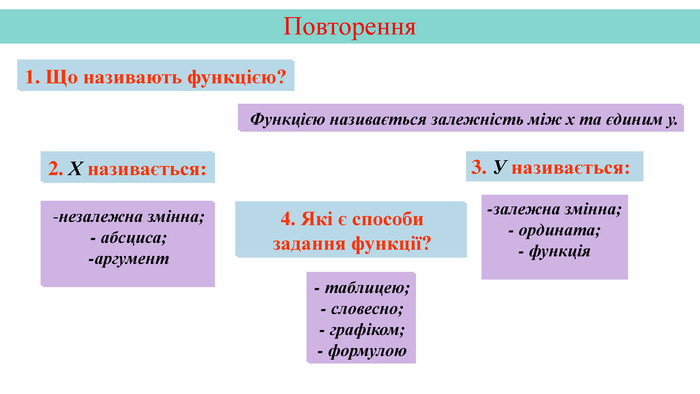
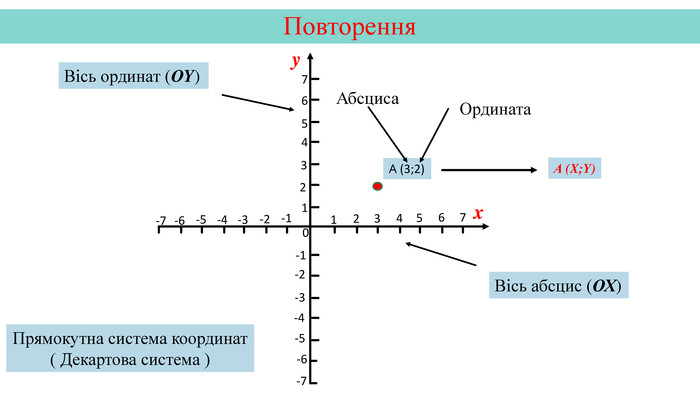
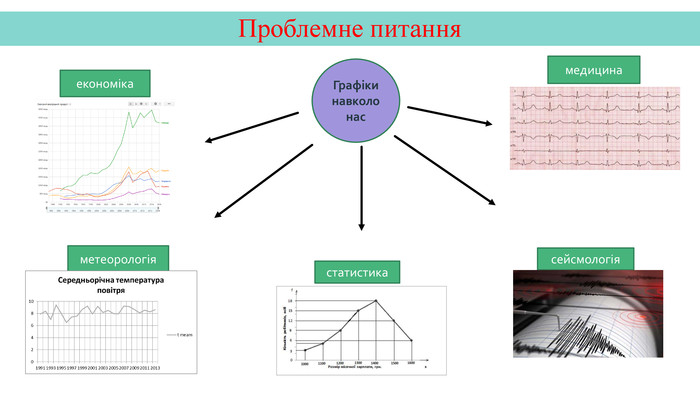
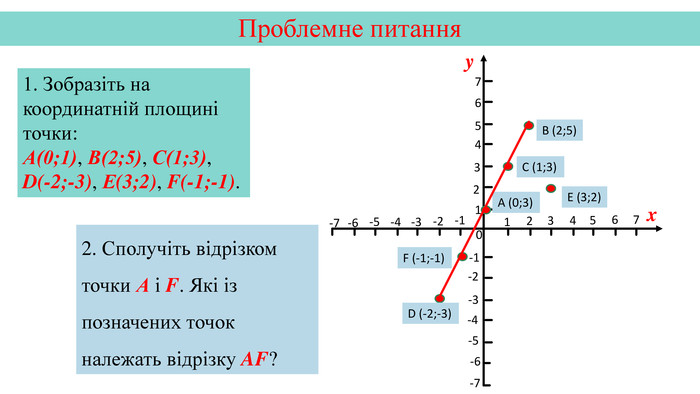
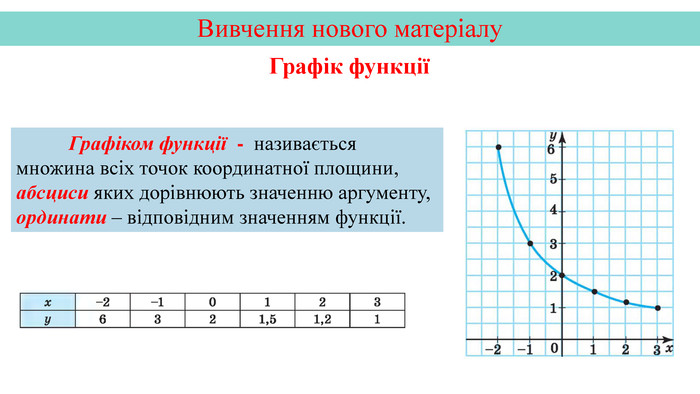
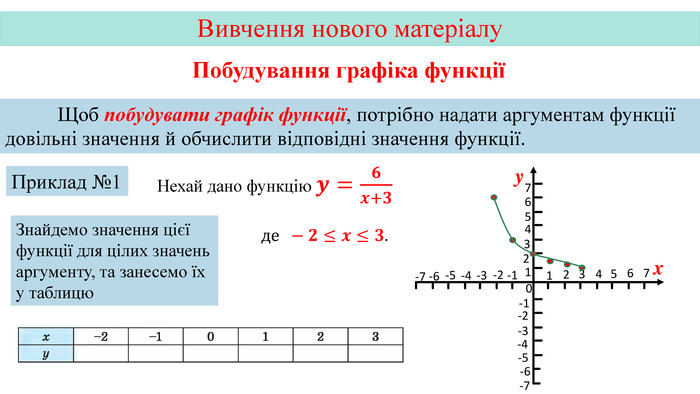
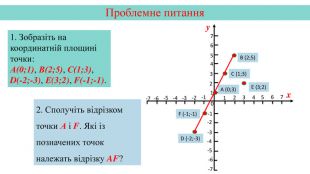
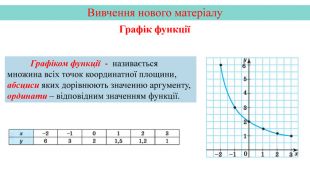
Презентація створена на тему "Графік функції" для кращої візуалізації побудови графіка.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку