Урок на тему: "Координати вектора"

Тема уроку: Координати вектора

Мета: домогтися свідомого розуміння учнями геометричного змісту поняття координати вектора; означення координат вектора; працювати над засвоєнням формули обчислення модуля вектора за його координатами; поповнити знання учнів додатковимии властивостями та ознакою рівності векторів за їх координатами; сформулювати вміння відтворювати вивчені твердження, а також виконувати дії відповідно до вивчених формул (знаходити координати вектора за координатами його початку та кінця, модуль вектора за його координатами), використовувати ці вміння під час розв’язування задач.

Тип уроку: засвоєння знань, умінь та навичок.

Наочність та обладнання: конспект «Координати вектора», комп’ютер, проектор

Вимоги до рівня підготовки учнів: описують координати вектора; застосовують вивчені означення і властивості до розв’язування задач.

Хід уроку

І. Організаційний момент

Перевірка готовності учнів до уроку, налаштування на роботу.

ІІ. Перевірка домашнього завдання

Три учні на дошці працюють з карточками. (Слайд 2)

Картка №1.

Накреслити два вектори рівні за абсолютною величиною і не колінеарні

Картка № 2

Накреслити два вектори, які мають рівні довжини і однаково напрямлені

Картка № 3

Накреслити два вектори які мають рівні довжини і протилежно напрямлені.

З остильними проводиться фронтальна бесіда. (Слайд 3)

1. Що таке вектор? Як позначаються вектори?
2. Які вектори називаються однаково напрямленими (протилежно напрямленими)?
3. Що таке абсолтна величнина вектора?
4. Що таке нульовий вектор?
5. Які вектори називаються рівними? Яку властивість мають рівні вектори?
6. Скільки рівних векторів можна відкласти від заданої точки, які дорівнюють даному вектору?
7. Які вектори називаються колінеарними?

ІІІ. Вивчення нового матеріалу

План вивчення теми

1.     Означення координат вектора. (Слайд 4)
2.     Позначення вектора та його координат. (Слайд 5)
3.     Координати нульового вектора.
4.     Вираження модуля вектора через його координати. (Слайд 6)
5.     Теорема (властивість і ознаки координат рівних векторів). (Слайд 7)

Координати вектора АВ, що має початок а точці А і кінець у точці В, дорівнює різниці координат точок В і А

Координати нульового вектора дорівнюють 0 (0; 0)

 Довжина вектора дорівнює квадратному вектору із суми квадратів його координат.

 Рівні вектори мають рівні координати. Якщо відповідні координати векторів однакові, то вектори рівні

ІV. Формування первинних умінь

1. Робота біля дошки

№ 446 (1, 2, 3)

А(2; 3), В(- 1; 4) АВ = (- 1 – 2; 4 - 3),  АВ = (- 3; 1)

А(3; 0), В(0; - 3) АВ = (0 – 3; - 3 - 0), АВ = (- 3; - 3)

А(0; 0), В(- 2; - 8) АВ = (- 2 – 0; - 8 - 0), АВ = (-2; - 8)

№ 447

А(1; 3), а(- 2, 1), ВА = а.  В - ?

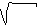
ВА(1 – х; 3 - у)= (- 2; 1)

 1 – х = - 2                 - х = - 2 – 1              - х = - 3             х = 3

 З – у = 1                   - у =  1 - 3                 - у = - 2            у = 2 

Відповідь: В(3; 2)

№ 450

А(3; - 4), В(- 2; 7), С(- 4; 16), D(1; 5). Довести СВ = DA

СВ = (- 2 + 4; 7 - 16) = (2; - 9)

DA = (3 – 1; - 4 - 5) = (2; - 9)

Відповідь: СВ = DA

2. Робота за готовим рисунком

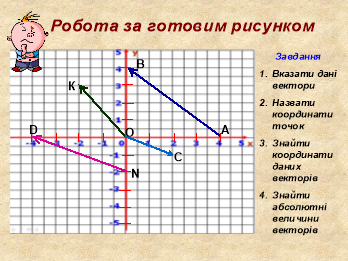
2. А(4; 0), В(0; 4), С(2; -1), O(0; 0), N(0; -2), D(- 4; 0), K(- 2; 3)
3. АВ(- 4; 4), ОК(-2; 3), ОС(2; - 1), ND(- 4; 2)
4. |АВ| = 4    2    , |ОК| =    13,  |ОС| =     5  , |ND|= 2    5
5. Практична робота

Сусіди по парті обмінюються зошитами. Там зоображають два різні вектори, потім зошит з рисунком повертають назад. Завдання - знайти координати векторів та модуль векторів, які зообразив сусід.

6. Гра «Знайдіть помилку»

АВ =   (2 – 3)² + (-1 - 4)²     =    26

V. Підбиття підсумків

Заповніть пропуски в тексті.

Кординатами вектора з початком у точці А(х₁; у₁) і кінцем у точці В(х₂; у₂) будуть числа х = ...., у = ... . Рівні вектори мають рівні ..., і навпаки ... . Модуль вектора а(а₁; а₂) дорівнює ... .

VІ. Домашнє завдання

§ 4 п. 13 вивчити № 449, № 451, №453(в.р.) стр. 120