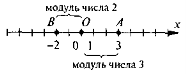
Урок на тему "Модуль числа"
Урок № 68. 6 клас
Тема. Модуль числа.
Мета: сформувати уявлення учнів про геометричний зміст поняття «модуль числа»;
формувати вміння читати, записувати вирази, що містять модуль, а також знаходити значення виразів, що містять числа під знаком модуль, розв’язувати рівняння та нерівності з модулем і позначати їх розв’язки на координатній прямій; розвивати логічне мислення, увагу, виховувати прагнення удосконалювати свої знання.
Тип уроку: засвоєння нових знань і вмінь
Обладнання: комп’ютер, презентація, підручник, таблиця.
Девіз уроку:Думай і роби, роби і думай.
І.А.Крилов.
Епіграф: Силу розуму надають вправи, а не спокій.
Папа Олександрівський.
Хід уроку
І. Організаційний етап
Організація уваги учнів.
ІІ. Перевірка домашнього завдання.
Оскільки вправи домашнього завдання мали суто репродуктивний характер, правильність їх виконання перевіряємо тільки у «слабких» учнів
ІІІ. Мотивація навчальної діяльності.
Працюватимемо гарно,
Щоб урок пройшов немарно.
ІV. Актуалізація опорних знань
Бліц-опитування
- Чи може шукана відстань бути від'ємним числом, нулем?
- Як пов'язана шукана відстань з координатами точки? Чи може відстань від початку відліку до заданої точки дорівнювати координаті цієї точки?
- Чи зажди відстань від початку відліку до даної точки дорівнює координаті точки? У яких випадках — ні? (Слайд 2)
Усні вправи
- Обчисліть
|
а) |
|
б) |
|
|
|
· 17 |
|
· 3 |
|
|
|
|
|
|
|
· 2 |
|
: 3 |
|
|
? |
|
? |
: 8
: 
-
Натуральним, цілим чи дробовим числом є -5, 1254567,
, 
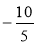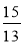, -3, 5?
-
Знайдіть значення виразу -7·(-7), - (+9), - (13), 0, -(-1),
.
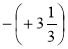Під час фронтального виконання усних вправ біля дошки працюють 3 учні, які розв'язують домашні задачі (Слайд 3)
Задача. Знайдіть відстань від початку відліку до точок координатної прямої А(-4), В(4), С(2), Е 
, D(2,5), О(0)
V.Формування теми і мети уроку. (Слайд 4)
VI. Вивчення нового матеріалу
Історична довідка: Для запису модуля числа вживається знак ||. Цей знак ввів у математику в середині ХІХ ст. німецький математик Карл Вейєрштрасс.
Термін “модуль” ввів англійський математик Р. Котес (1682 - 1716).
Слово “модуль” походить від латинського слова “modulus”, що означає “міра”.
Поняття модуля вводимо, виходячи з геометричних міркувань, а потім уже на прикладах з'ясовуємо, що:
а) модуль додатного числа є це саме число,
б) модуль нуля є нуль (це ж саме число),
в) модуль від'ємного числа є число, протилежне до даного числа.
Важливо також, виходячи з геометричних міркувань і поняття «протилежні числа», підкреслити, що:
а) модуль даного числа — це єдине число, але,
б) однаковий модуль мають 2 протилежних числа.(Слайд 6 )
|
|
|
|
Модуль числа |
|
|
1. Модуль числа а — це відстань від початку координат до точки А (а) 2. Позначають |-21, |31, \а | 3. Властивості: 1) |0| = 0, 2) | а | = а, якщо а додатне, 3) | а | = -а, якщо а від'ємне, 4) якщо | х | = а, де а — додатне число, то х = а або х = -а |
Приклад
1. 2. | х | = 3, тому х = 3 або х = -3 3. Обчисліть значення виразу:
| 0 | + |
· | 2 | = 0 + 
· 2 = 0 +7 = 7
(Слайд 7,8,9 )
VІІ. Застосування знань. Формування вмінь
№1 Вправи на використання означення модуля і його властивостей.
Усні вправи
№ 987
№ 989
Письмові вправи
Задача 1. Знайдіть модулі кожного з чисел:
81; 1,3; -5,2; 
; 
; 
; -52; 0. Запишіть відповідні рівності.
Задача 2. Знайдіть значення виразу |х|, якщо х дорівнює:
а) -12,3; б) -66; в) 83; г) -
; д) 3
; е) -6
.
№2 Самоконтроль своїх знань.
Робота за підручником.
№ 994;
№ 997;
№ 1006.
Задача 3. Знайдіть: а) від'ємне число, модуль якого дорівнює 25; 
; 7,4;
б) додатне число, модуль якого дорівнює 12; 1; 
; 3,2;
в) додатні і від'ємні числа, модуль яких дорівнює 8; 5
; 19,2; 0.
(Слайд 10,11, 12 )
Задача 4. Розв'яжіть рівняння: а) | х | = 6; б) | х | = 8; в) | х | = 0.
№1011 – запис на дошці
№3 Поглиблення знань
«Мудрі завдання» випереджальні завдання
№1 Розв’язати рівняння
│2│х│-3│=9
№2.Знайти усі цілі числа, які є розв’язками нерівності. (Слайд 13 )
А)│х│≤5,б)│х│<3
VІІІ. Підсумки уроку.
Самостійна робота (Слайд 14)
За опорним конспектом повторюємо зміст вивчених понять.
Ігровий момент.
Я задумала два протилежних числа. Поставте тільки одне запитання, щоб дізнатись ці два числа.
(Слайд 15)
ІХ. Домашнє завдання
§23, № 988, 995 1005, 1008, 1012.
Х. Рефлексія.
(Слайд16)
Як би ти оцінив свої здобутки на уроці:
— «Я все зрозумів, я все роблю правильно».
— «Мені була зрозуміла більша частина матеріалу, але я ще іноді
допускаю помилки».
— «Я майже нічого не зрозумів, нова тема для мене дуже складна».
(Слайд 17).
про публікацію авторської розробки
Додати розробку