Урок на тему:"Похідна. Практичні задачі"

Урок з алгебри в 11-му класі.

Розроблено та проведено вчителем математики

 ЗОШ № 7 ім. В. В. Бражевського м. Житомира

Сергієм Олександровичем Сафонюком

Для перевірки, як учні знають і вміють застосовувати формули, проводиться математичний диктант.  

Правильні відповіді

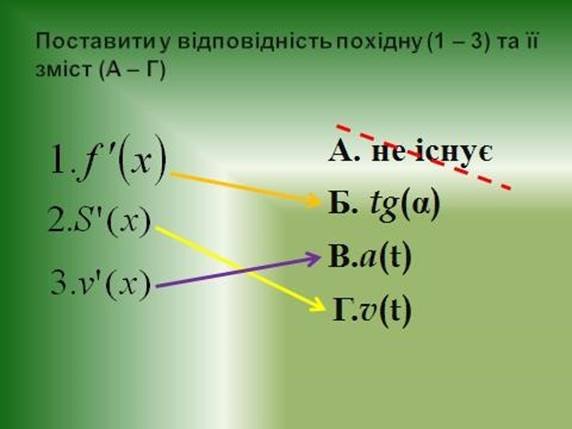
Використовуючи геометричний зміст похідної, дати відповіді на наступні завдання.

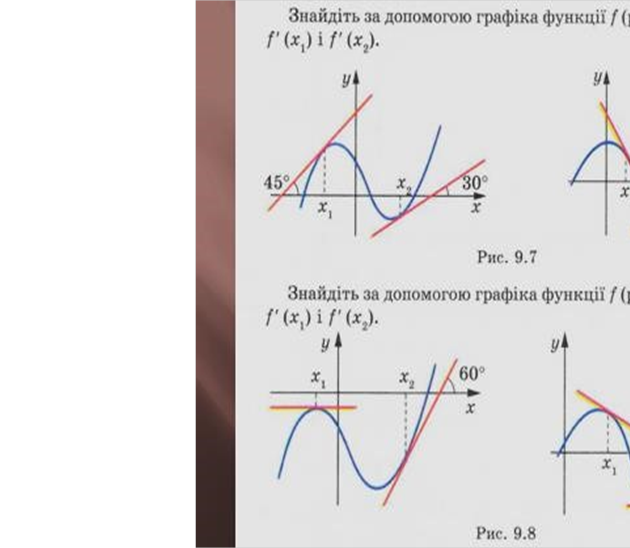
Розв’язок

Рис. 9.7 а)                                                                       

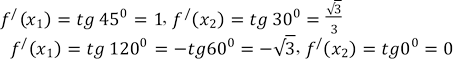б)                                                                                             

Рис. 9.8 а) 𝑓^/(𝑥₁) = 𝑡𝑔0⁰ = 0, 𝑓^/ (𝑥₂) = 𝑡𝑔60⁰ = √3

               б)

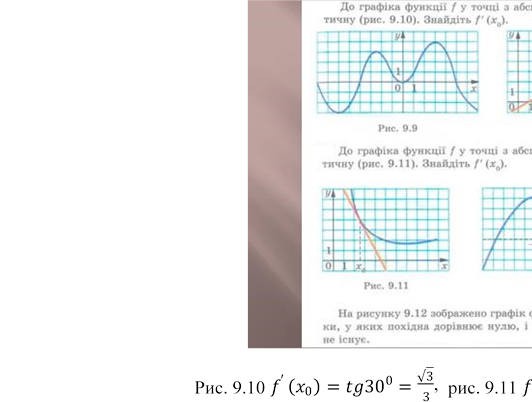
Рис. 9.12 𝑓^′(−3) = 𝑓^′(2) = 0. В точці х = 4 похідна не існує, тому що в ній  не існує дотичної.

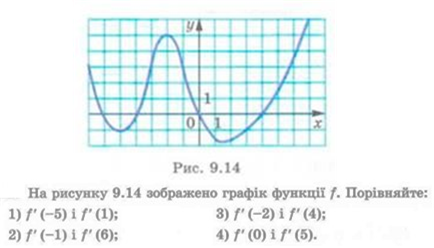
1) 𝑓^′(−5) > 𝑓^′(1); 2) 𝑓^′(−1) < 𝑓^′(6);   3) 𝑓^′(−2) < 𝑓′(4)

4) 𝑓^′(0) < 𝑓^′(5).

Повторимо алгоритм знаходження max і min функції

1.   Знаходимо похідну функції

2.   Прирівнюємо похідну до нуля і знаходимо критичні точки, які відмічаємо на числовій прямій

3.   Встановлюємо знаки похідної на кожному з проміжків

4.   Якщо при переході через точку похідна змінює свій знак з « - » на « + », то це точка максимуму, якщо « + » на « - », то це точка мінімуму. Якщо знак не змінюється, то ця точка не є ні максимумом, ні мінімумом.

Розглянемо домашнє завдання. 

Учням було запропоновано з листа картону розмірами  8 х 8 см зробити відкриту коробку найбільшого об’єму. Розв’яжемо цю задачу для загального випадку. 

Розв’язання

Нехай ми відріжемо в кутах картону  квадратики зі стороною х см.

Тоді розміри коробочки становитимуть . 𝑉 = (𝑎 − 2𝑥) ∙ 𝑥 = 𝑎 𝑥 − 4𝑎𝑥 + 4𝑥 → 𝑚𝑎𝑥.

𝑉’(𝑥) = (𝑎²𝑥 − 4𝑎𝑥² + 4𝑥³ )^′ = 12𝑥² − 8𝑎𝑥 + 𝑎²

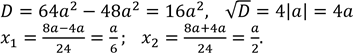, (а – сторона).

Отримані критичні точки відмічаємо на прямій і встановлюємо знак похідної на отриманих проміжках.

   +   max -    min      +

Відповідь: необхідно вирізати квадратики зі стороною  

Знаходження max і min функції часто застосовують при розв’язуванні прикладних задач. 

Розглянемо деякі з них.

Розв’язання

Сила струму -.

Потужність - 𝑃 = 𝐼 ∙ 𝑈 = 𝐼² ∙ 𝑅.

З іншої формули маємо - , де ε – електрорушійна сила, 

R – опір реостата, r – внутрішній опір джерела. Тоді потужність будемо знаходити за наступною формулою .

Складемо функціональну залежність 𝑃(𝑥). Позначимо R = x.

. Для знаходження максимального значення потужності

знайдемо P′(x).

′

.

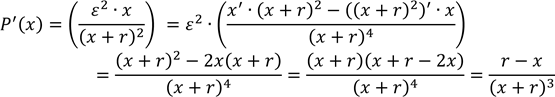 Знайдемо критичні точки..

         +     max -  

r

Отже, потужність буде найбільшою при умові рівності опору реостата і внутрішнього опору джерела, тобто R = r.

Розв’яжемо наступну практичну задачу.

Розглянемо математичну модель задачі.

                        За умовою 𝑆 = 𝑘𝑥𝑦², де 𝑆 – міцність, k – сталий коефіцієнт,                            х, у – ширина і висота балки відповідно.

  а     у         З прямокутного трикутника маємо: 𝑦² = 𝑎² − 𝑥².                    Складаємо рівняння залежності      х              𝑆(𝑥) = 𝑘𝑥(𝑎² − 𝑥²) = 𝑘𝑎²𝑥 − 𝑘𝑥³

𝑆^′(𝑥) = 𝑘𝑎² − 3𝑘𝑥² = 𝑘(𝑎 − 𝑥√3)(𝑎 + 𝑥√3)

                        𝑆^′(𝑥) = 0

                        .

                  За умови невід’ємності розмірів балки беремо .

+       max       −

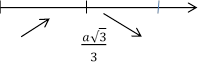           0       

 .

   Відповідь: розміри балки  .

   Для розв’язування практичних задач досить суттєву допомогу надають математичні моделі.

Задача. Вікно має форму прямокутника, завершеного півкругом. Периметр вікна дорівнює а. При яких розмірах сторін прямокутника вікно буде пропускати найбільшу кількість світла?

Розв’язування

х                          Нехай радіус півкола дорівнює  х. Тоді сторона       В                            С    ВС = 2х. Виразимо сторону АВ через х і периметр а.   

             х х                P= (𝐴𝐵 + 𝐵𝐶) ∙ 2 + 𝜋𝑙 = (𝐴𝐵 + 2𝑥) ∙ 2 + 𝜋𝑥

                                           .

                                           Площа вікна складається з площі прямокутника і площі півкруга. Складаємо залежність S від x.

    A                             D     𝑆^′(𝑥) = 𝑎 − 2𝑥(4 + 𝜋) + 𝜋𝑥 = 0

.        +    max -               BC = 2x , AB=.

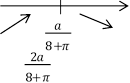Відповідь: вікно повинно мати форму квадрата зі стороною       .

Задача. Пункти А, В і С розміщені у вершинах прямокутного трикутника з прямим кутом С. ВС = 3 км, АС = 5 км. З А в С веде шосейна дорога. Турист починає рухатись з А по шосе. На якій відстані від пункту А турист має звернути з шосе, щоб за найменший час дійти з А до В, якщо швидкість туриста по шосе дорівнює 5 км/год, а поза шосе – 4 км/год?

                                    В Розв’язання

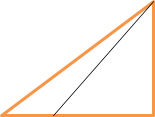Розглянемо Δ АВС ( < С = 90⁰ ). АС =5, ВС = 3.                                                    Точка М – місце сходження туриста з шосе.                                                    Нехай АМ = х, тоді МС = 5 – х. За теоремою              х       5-х Піфагора МВ² = МС² + ВС² =>

А           М                   С МВ=. Час, який витратить турист,                 на подолання відстані АМ дорівнює ^𝑥, на подолання відстані МВ -

5

. Тоді матимемо таку залежність .

,

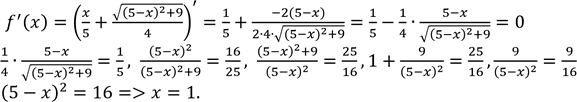Відповідь: на відстані 1 км.