Урок на тему: "Пропорція. Розв'язування вправ"

Про матеріал

Метою даного уроку є розширити знання учнів про пропорцію та її властивості, показати зв'язок теми з іншими сферами , ознайомити з поняттям "золотий переріз" .

Перегляд файлу

МАТЕМАТИКА

N245 (393), ГРУДЕНЬЛ)

ПРОПОРЦШ

6 клас

М.НОЧЕВЧУК, учителька математики ЧерВоногран;тнянсько7 ЗОШ l—ll cmyneHiB,

Тема. Розв'язування вправ.

Мета уроку: повторити означення проосновну формувати навички розв'язування вправ на знаходити мий член ознайомити з поняттям «золотий показати зв'язок теми з розвивати математичну мову i бажання нове; виховувати iHTepec до математичних знань, почуття прекрасного.

Обладнання: «абаки» , картки i3 завданнями для роботи i картки для роботи на таблиця «Пропортрет таблиця i3 зображеннями репродукцй картин i споруд.

ХЩ УРОКУ

1. навчально7

М атематика створювалася людським розумом упродовж багатьох i продовжуе розвиватися, а й застосування охоплюють все кола бутгя. Математика — велика книгалюдського дос-

На ви про одну сторПжу llieT велико; книги.

Найкращий вивчити i запам' ятати — це

зробити	самому. Будемо робити
тя. А	вам нададуть слова видатних
людей,	на Прочитайте Тх.
Хто	не знае, тому нг в чому помилятися. Менандра (342-291 до н.е.), давньогрецький поет
Щоб	до мети, треба перш за все йти. Оноре де Бальзак (1799—1850), французький письменник

ВолоДарсько-Волинський р-н, Житомирська обл.

II. опорних знань.

Що об'еднуе собою рух транспорту i кувиготовлення i роботи, викреслювання карт i розглядання Mikp06iB у Комусь таке запитання може здатися дивним. Але учень шостого класу може так: у BCix названих справах i процесах часто використовуються Як продопомагають розв'язувати pi3Hi ви коли будете уважними на чи ви йти вперед.

1. Перехресне опитування (2—4 хв).

(Застосовуеться таблиця речення.

1-й учень (звертаеться до 2-го учня). В

Якщо ви боятеся зробити помилку, не можете знайти то прочитайте слова ще раз. I вони додадуть вам i ви будете працювати

Вашу роботу на ypoui я буду вати не за дванадцятибальною системою, а iHaкше. Як саме, про це ви у уроку. Ваша i будуть BpaxoBaHi.

добуток
2-й учень. добутку	(Звер-
таеться до 3-го учня) Цю юты...	назива-
3-й учень. Основною 2. Математичний диктант.	пропорцй.
Один учень працюе	дошки,

решта — у зошитах. У зошитах записуються лише

1. вјдношення:

а) 35 до 7;

б) 10 до 7;

в) 2 до 35.

10 N245 (393), ТРУДЕНЬЛ) МАТЕМАТИКА

2. piBHicTb ДВОХ

а) 35 до 7i 10 до 2;

б) 10 до 5i 15 до 5;

в) 2 до 10 i 7 до 35. piBHocTi

раховуеться 1 бал, i набрана kiJIbkicTb виставляеться за математичний диктант. Учитель обходить ряди, контролюючи процес взаемо-

надае

Учитель. Тема уроку «Розв'язування вправ

на «призначить вам побачення» на уроках алгебри, геометрй,

ки, xiMii, малювання та музики. 13 задачами, розв'язування яких зводиться до складання пропорцй,

люди починаючи домогосподарки, вченими у галузях науки.

III. Розв'язування вправ.

Yci одержали картки i3 завданнями 1. Ti, хто забажав працювати одержа-. ли картки i3 завданнями 2 i виконують ix у зо-

шитах

Завдання 1

1. де ви двох

не використовуючи поняття про-

(При

—

2 10

3' 25

2. з даних е Чому?

1) 30 • 5 -42 : 7; 2) 10:5;

4) 0,5 : = 24 + 5;

36 24 5

9 6 10

записують за допомогою «a6akiB», а аргументують

З. Прочитати : 6 = 24 : 8.

(Спочажу читають тихо по парах, а один учень за бажанням читае голосно,)

Цей запис можна прочитати:

24 до 8»,

« 8, на 8»,

«18 до 6, як 24

вали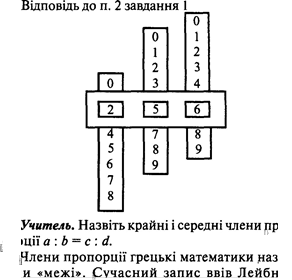

(1708 р.)

про-

1-й cnoci6

18 : 3 i 24 : 8 = 3, тобто значення i правот частин е одне й те саме число З.

Це за означенням

2-й cnoci6

до kiJIbkocTi

в uraci якщо

Учитель. Що означае запис — ?

на 4; час-

до 8».

Як це

можна тлумачити?

(Його можна тлумачити так: перше число складаеться з трьох однакових частин, а друге — з

чотирьох таких самих частин.) задачу двома способами.

1-й cnoci6

3MicT

Копчики

Розв'язання

1) 20 : 4 = 5 — становить одна частина.

2) 3 + 4 = 7 (частин) — становлять yci класу.

2-й cnoci6

Хлопчики

частин

Розв'язання

3-20

4 х = 15,

20+ 15 =35.

8. Задача. Роки батька до P0kiB сина як 8 : З. P0kiB якщо батьk0Bi 48 pokiB?

Розв'язання

	Роки	Частини
Батько	48	8
Син	х	З

48-3

8 х = 18.

18 P0kiB.

9. Знайти значення а, при якому буде правильною:

а а а) 6) в)

16 а 16 4

Учитель. розчину називаеться маси розчиненоТ речовини до маси розчину. Ii виражають у

Задача. У 160 г води розчинено 40 г Знай-

200

20 %.

Заддання 2

1. дробових чисел

шенням

6) 0,75 : 0,15.

2. Знайти

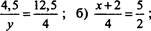2х-1

а) в)

З 2

З. Знайти для трюх даних чисел 10, 16, 3 чет-

верте число.

4. У 800 г розчину 40 г у 100 г розчину?

5. розчину — 10 %. Скђ1ьки в 4 кг розчину?

IV. пауза.

Учитель. Сидячи за партою, Руки на napTi, в кулаках,

Зробимо вправу, так:

стискаемо i розтискаемо,

Мов ми yci розминаемо.

Будемо вправу з вами

Легше буде тепер працювати.

А тепер розв' таку задачу з YkpaiHcbk0i

мови.

Задача. Число сто позначають трьома цифрами, назву цього числа — трьома Яке ще число мае однакову цифр i що означають назву цього числа?

(1 000 000,

Що означае крилатий вираз «Золота середи-

(Вживаеться д.пя характеристики людини, що уникае

У. Застосування математичних знань на прак-

менша частина

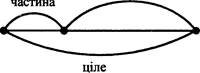
ти розчину.

Розв'язання

1) l60 + 40 = 200 (г) — маса розчину.

12 FE45 (393), ТРУДЕНЬШ МАТЕМАТИКА

(Менша частина) : частина) = частина) :

Цей називають золотим або золотою або в крайньому i середньому

Задачу про золотий nepepi3 формулюють ще так: або даний а на такЈ частини, щоб з них х була мЬк yciM i йот меншою частиною, тобто так, щоб справджувалася а х

а х

— = 1,618 , його називатъ х

шенням золотого nepepi3y».
У BikV1 вважали людини , для яко; було характерне	такоТ
ня золотого nepepi3Y. Нехай висота	люди-

н и АВ, точка Х мае лежати на талй, тобто повинна виконуватися

Учитель. Давайте виберемо серед вас претенна конкурс краси рюемо частни тои, nepeBiIW€M0 виконання проЗ Bik0M людини значення

За допомогою розв'язували pi3Hi ще в часи. Повну пробуло створено в Грецй в lV сг. до н.е. в основному працями видатних давньогрецьких учених Евдокса i Теетета. Цю докладно виклав у «Началах». Там доведено i основну пропорцй (lIl ст. до н.е).

Учення про i старо-

греки називали музикою, яку вважали галуззю математики. Вони знали, що чим слабше натягнуто струну, тим нижчий («товщий») звук, який вона дае, а чим натягнуго струну, тим вищий вона дае звук. Але в кожному музичному ii-tcrpy»qemi кЈњка струн. yci струни

час гри звучали приемно для вуха, довжини струн перебувати в певному

TepMiH походить латинського слова proportionalis, яке означае «такий, що мае правильне Mix частинами i шо перебувае в певному до деяко7 величини»З

що ми в машину часу i опинилися в MicTi в епоху Пройдемося вулицями i площами, заглянемо у

(Демонструються репродукцЈТ картин i фо-

старовинних ь. ) картини, скульптури, храми для нас € зразками гармонй. Це пояснюеться тим, що прекрасного знали шення частинами тобто ня золотого nepepi3Y.

TepMiH «золотий перерЈз» YBiB Леонардо да ХУ ст. Портрет Мони який BiH намалював, базу€ться на властивостях золотого nepepi3Y.

греки вважали, що прямокутники, довжини сторјн яких утворюють

ня золотого для ока. прямокугник, cTopiH якого l,61 8, називають «золотим».

Якшо було розбити на двЈ частини прямокутний (наприклад, одну смугу

травою, а другу — то смуги робити однаковоТ ширини. Краще, якщо смуги у

Це числа Якщо взяти калькулятор i кожне з них на попередне, то одержимо значення, до значення золотого

МАТЕМАТИКА N245 (393), [РУДЕНЬ2ОО6 13

Проведемо експеримент. 13 даних прямокутой, що вам подобаеться.

2() см

40 см

35 см

дають психолог Фехнер у 1876 р. проводив Taki BiH показував багатьом людям прямокутники pi3H0i форми, просив вибрати серед них форму, що Тм подобаеться. Переважна вибирала прямокутник i3 cTopiH, яке золотого У наш час американський лог Мак- Каллок. Результати були Taki caMi.

Виявляеться, що вписуеться у «золотий» прямокутник, сприймаеться легше, е приемною для очей HaBiTb на

5 ще в 1925 р. мистецтвознавецьЛ.Л.Сабанеев, 1770 музичних TBopiB 42 ав-

TopiB, виявив, що переважну видатних творјв можна легко на частини або за темою, або за будовою, або за ладовим строем, 51ki перебувають собою у золотого Чим

ший композитор, тим у його TBopiB знайдено золотий У Бетховена, Моцарта, Шопена i Шуберта знайдено у 90 % BCix TBopiB.

Цей результат Сабанеев на BCix 27 етюдах Шопена. BiH знайшов у них 178 золотих nepepi3iB.

У наш час золотий застосовуеться у у проблем.

ПовЈДомлення 6

З люди намагаються дати озна-

чення поняття «щастя», виявити «елементи», з яких воно складаеться. Вдаеться такий погано, 60 у кожного свое уявлення про щастя. Але кожна людина може сказати, чи щаслива вона.

“7,2.

Ф. Шопен

Вивчаючи анкет, визначили щасливих i нещасних людей. показав, що людей, задоволених i незадоволених обставинами свого життя, ряеться «золотого nepepi3y».

Учитель. Вважають, що у золото; пропорцй у VI ст.

до н.е.

належне здоровому i брав участь у кулачному бою на 58-й

548 р. до н.е. 1снуе легенда, що через малий

3PiCT не допускати до змагань.

— Можливо, — промовив — вигляд i не викликае у вас Але я буду наносити удари з такою математичною що стане жарко. Моя глибока Bipa в число — це мое життеве кредо.

BiH додержав свого слова — став з цього виду спорту.

створив школу в м. kpoT0Hi, яка майже тридцять P0kiB i здобула велику попудосягненнями в математики. Статуг школи був дуже суворий. Потрапити до школи могли p03YMHi, та стаpaHHi

Греки вважали за честь навчатися в

ра математики.
А зараз ми	хто з вас	стати
учнем школи	це Ti	показа-
ли на	знання i набрали

(Протягом уроку кожного учня.)

Yci одержують особливий знак — пентаграму (правильний п'ятикутник, i3 кольорового паперу).

14 N245 (393), ПУДЕНЬ2Ш6 МАТЕ ТИП

вважав пентаграму незвичайною i дарував й зображення друзям як символ дружби. п' ятикутника утворюють 3ipkY, яку вважали символом здоров'я. Правильний п'ятикутник був емблемою Тх союзу i ним знаком. Користуючись вони один одного. За переказами, один тяжко 3axBopiB на i не перед смертю розрахуватися з який його доглядав. BiH запропонував на CTiHi будинку намалювати п'ятикутник. Через P0kiB який подорожував побачив п'ятикутник, в господаря про те, що трапилося, i щедро його нагородив.