Презентація "Функція та її властивості" (9 клас)
Про матеріал
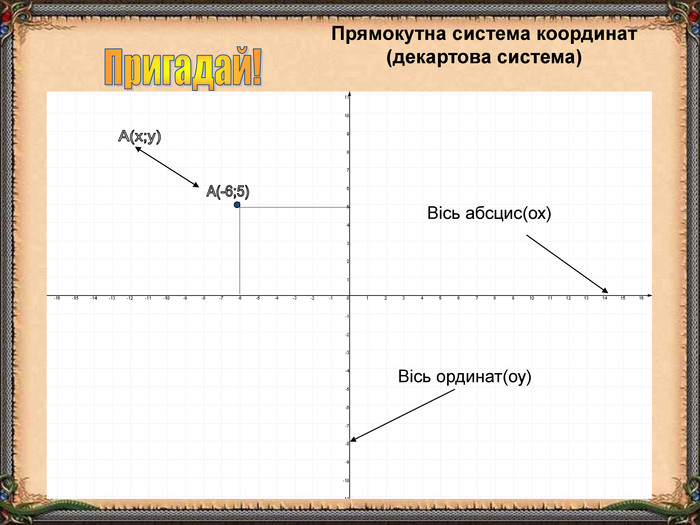
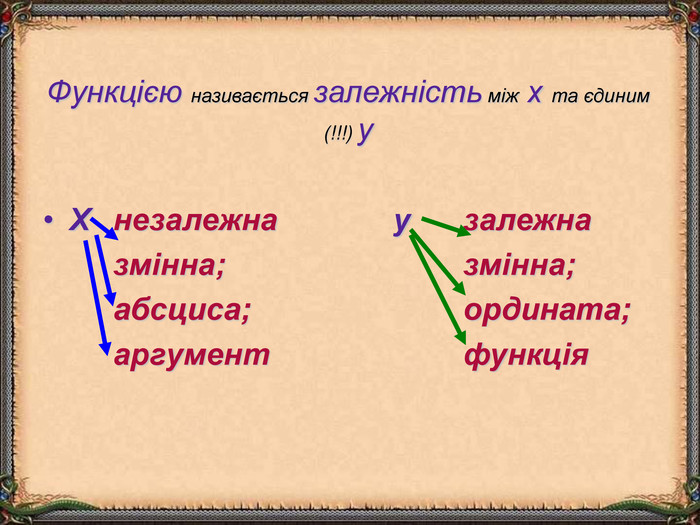
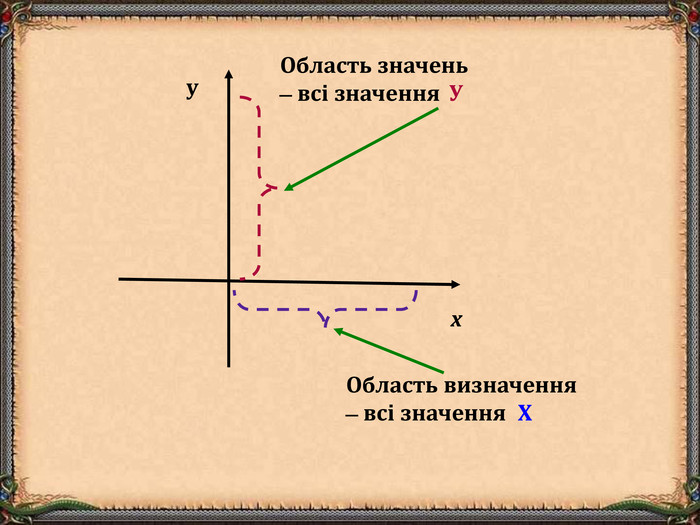
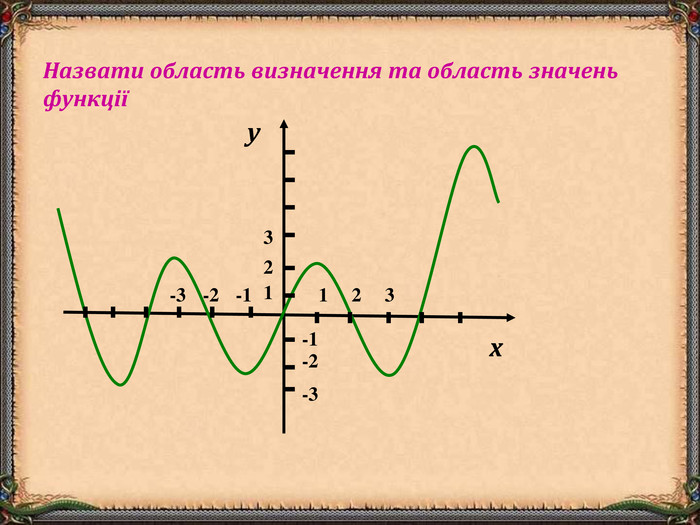
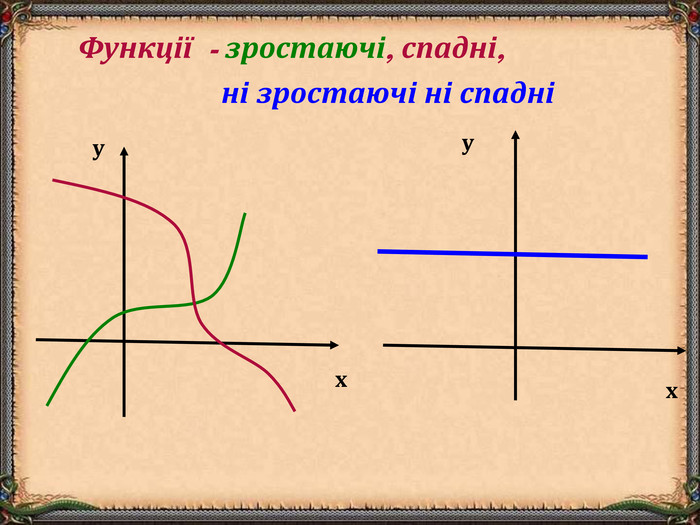
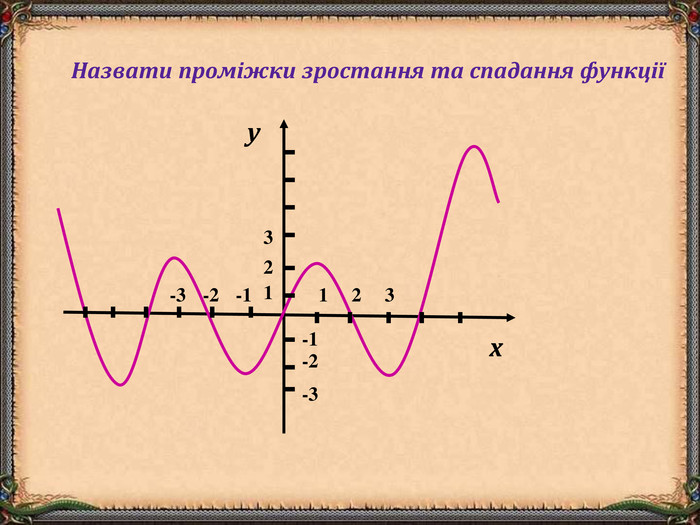
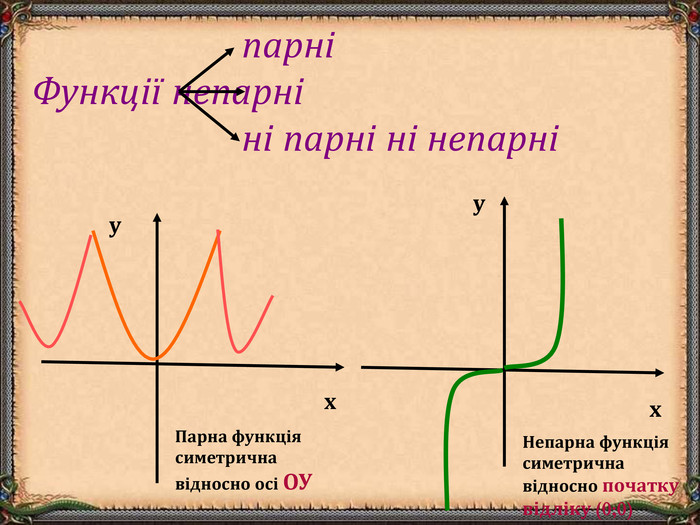
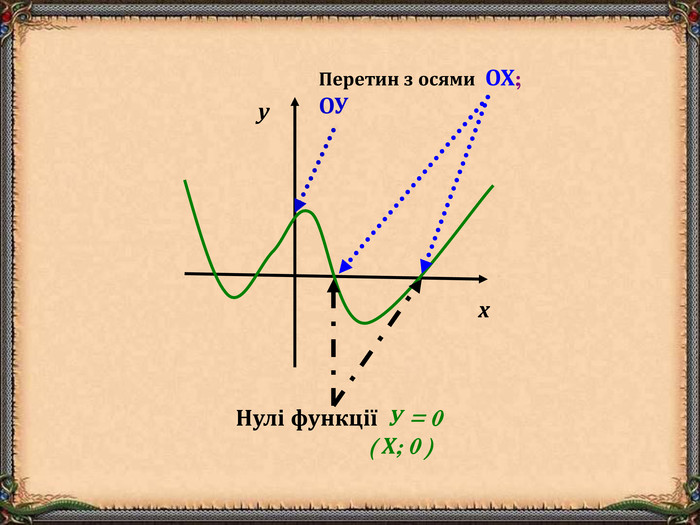
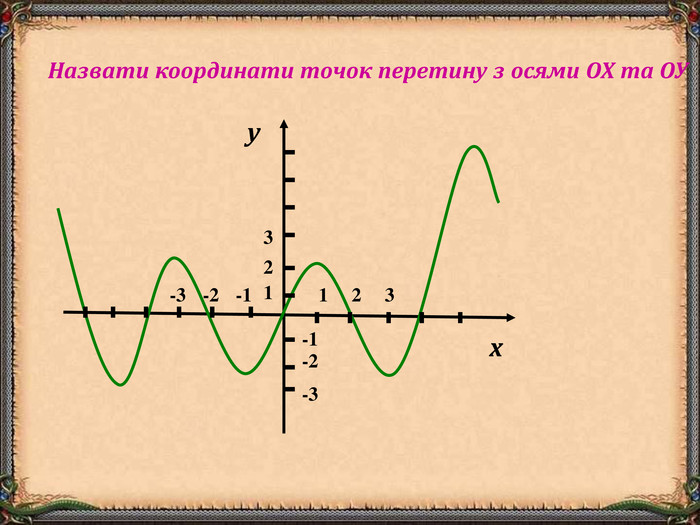
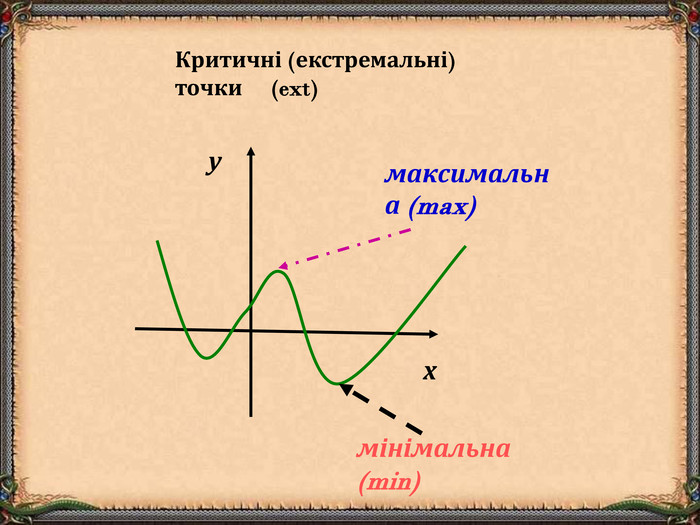
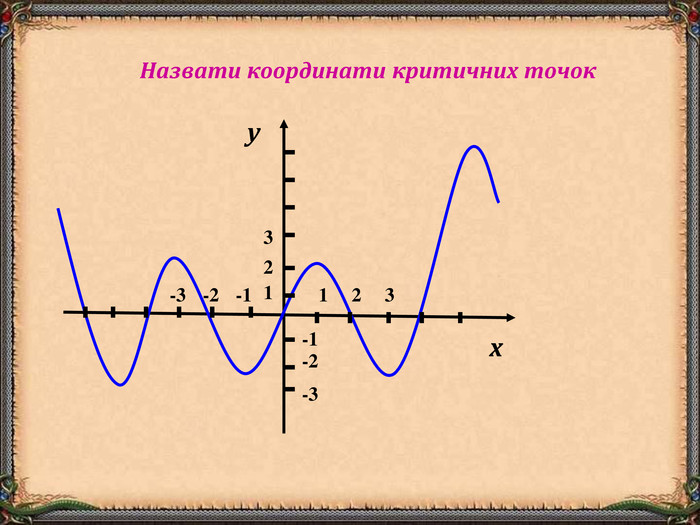
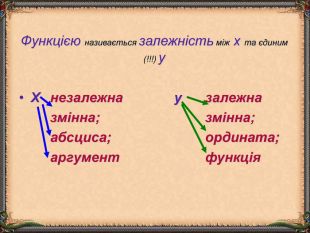
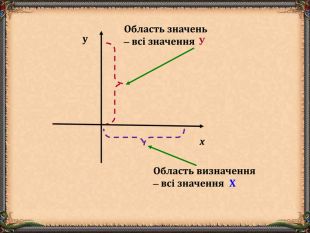
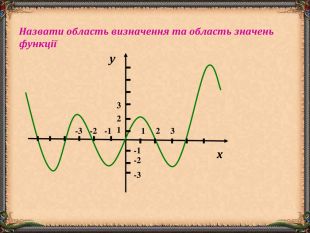
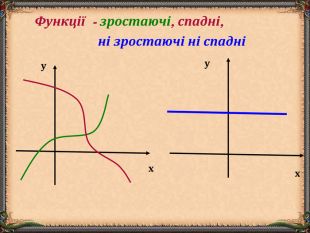
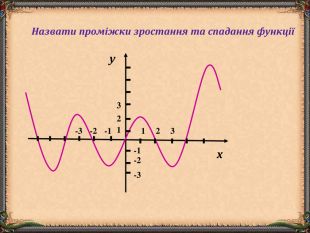
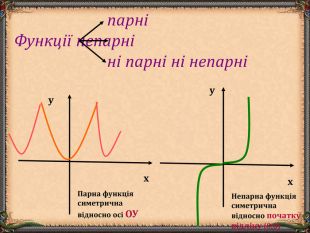
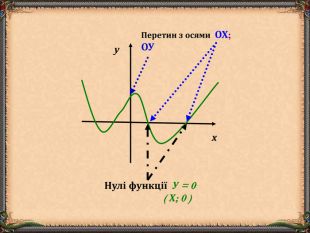
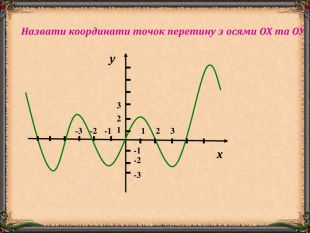
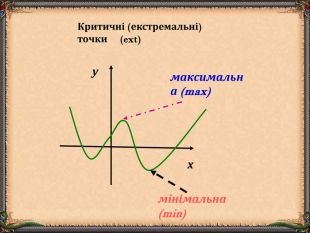
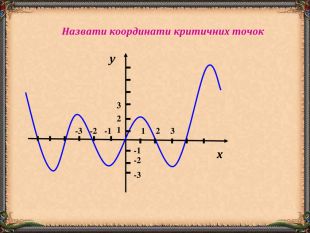
В презентації "Функція та її властивості" (9 клас) розглянуті питання властивостей функції (означення, способи задання, основні точки, проміжки зростання та спадання функції, історичні відомості).
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку













-

Водяницька Лариса
10.10.2023 в 08:18
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Личко Вікторія Михайлівна
05.12.2021 в 12:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Зінченко Валентина Сергіївна
02.11.2021 в 22:40
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Shaga Tanya
18.03.2021 в 10:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Скляр Юлія Олексіївна
22.11.2020 в 22:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Горик Руслана Миколаївна
22.11.2020 в 18:09
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 3 відгука