Урок на тему «Розв’язування прямокутних трикутників»

Контрольна робота з теми «Розв’язування прямокутних трикутників»

Варіант І

1. (1 б.) Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють 12 см і 35 см.
2. (1 б.) Знайдіть невідомий катет прямокутного трикутника, якщо його гіпотенуза і другий катет відповідно дорівнюють 17 см і 8 см.
3. (1 б.) АВ – гіпотенуза прямокутного трикутника АВС, АС=5 см, <В=47˚. Знайдіть АВ з точністю до сотих.
4. (2 б.) Побудуйте прямокутний трикутник. Знаючи, що катети даного трикутника дорівнюють 5 см і 12 см, знайдіть його гіпотенузу, sin, cos і tg всіх його гострих кутів.
5. (2 б.) Діагоналі ромба дорівнюють 16 см і 30 см. Знайдіть периметр ромба.
6. (2 б.) Розв`яжіть прямокутний трикутник ΔАВС (<С=90˚), знаючи, що АВ=8 см, а АС= 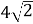см.
7. (2 б.) З точки до прямої проведено дві похилі завдовжки 10 см і 14 см, різниця проекцій яких дорівнює 8 см. Знайдіть проекції похилих та відстань від точки до прямої.

Додаткове завдання: Сторони трикутника дорівнюють 13 см, 14 см і 15 см. Знайдіть проекції двох менших сторін на більшу сторону.

Контрольна робота «Розв’язування прямокутних трикутників»

Варіант ІІ

1. (1 б.) Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють 12 см і 5 см.
2. (1 б.) Знайдіть невідомий катет прямокутного трикутника, якщо його гіпотенуза і другий катет відповідно дорівнюють 41 см і 40 см.
3. (1 б.) АВ – гіпотенуза прямокутного трикутника АВС, АС=7 см, <В=53˚. Знайдіть АВ з точністю до сотих.
4. (2 б.) Побудуйте прямокутний трикутник. Знаючи, що катети даного трикутника дорівнюють 8 см і 15 см, знайдіть його гіпотенузу, sin, cos і tg всіх його гострих кутів.
5. (2 б.) Діагоналі ромба дорівнюють 24 см і 70 см. Знайдіть периметр ромба.
6. (2 б.) Розв`яжіть прямокутний трикутник ΔАВС (<С=90˚), знаючи, що АВ=8 см, а ВС= 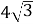см.
7. (2 б.) З точки до прямої проведено дві похилі, різниця яких дорівнює 2 см. Знайдіть ці похилі та відстань від точки до прямої, якщо проекції  похилих дорівнюють 1 см і 5 см.

Додаткове завдання: Сторони трикутника дорівнюють 25 см, 29 см і 36 см. Знайдіть проекції двох більших сторін на меншу сторону.