Урок на тему «Розв'язування задач підвищеної складності на застосування теорії подільності многочленів»
Тема: Розв'язування задач підвищеної складності на застосування теорії подільності многочленів
Мета: систематизація та поглиблення знань учнів з теорії подільності многочленів, вдосконалення умінь та навичок застосування теорії під час розв'язування задач підвищеної складності; розвиток творчих здібностей, нестандартного мислення; виховання інтересу до математики
Цикл уроків з алгебри на тему «Основи теорії подільності»
для 8 класів з поглибленим вивченням математики
підготувала вчитель математики
НВК: Гайсинська СЗШ-інтернат І-ІІІ ступенів - гімназія
Дем´янюк Ганна Володимирівна
Урок № 16
Тема: Розв’язування задач підвищеної складності на застосування теорії подільності многочленів
Мета: систематизація та поглиблення знань учнів з теорії подільності
многочленів, вдосконалення умінь та навичок застосування теорії під час розв’язування задач підвищеної складності;
розвиток творчих здібностей, нестандартного мислення;
виховання інтересу до математики
Тип уроку: Вдосконалення знань, умінь та навичок
Обладнання: картки із завданнями
Хід уроку
1.Актуалізація опорних знань
- Виконання усних вправ:
-
Визначити степінь многочлена , який утвориться після розкриття всіх дужок та зведення подібних у виразі
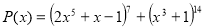 , назвати старший коефіцієнт та вільний член.
, назвати старший коефіцієнт та вільний член.
-
Доведіть, що многочлен
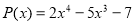 ділиться націло многочлен
ділиться націло многочлен  .
.
-
Чи може многочлен
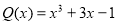 мати раціональні корені?
мати раціональні корені?
- Індивідуальні завдання:
-
Не розв’язуючи корені
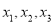 многочлена
многочлена 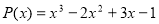 , знайдіть значення виразу
, знайдіть значення виразу 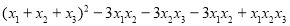 .
.
-
Доведіть, що функція
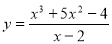 набуває цілих значень для всіх цілих значеннях аргументу.
набуває цілих значень для всіх цілих значеннях аргументу.
Останні дві задачі пропонуються індивідуально двом учням для розв’язування на дошці в той час, коли усно розвязуються задачі 1-3. Під час виконання задач акцент робиться на теоретичні факти, які застосовувалися для розв’язування.
2. Етап формування умінь та навичок
- Задача
Остачі від ділення многочлена ![]() на двочлени
на двочлени ![]() і
і ![]() відповідно дорівнюють
відповідно дорівнюють ![]() і
і ![]() . Знайдіть остачу від ділення многочлена
. Знайдіть остачу від ділення многочлена ![]() на многочлен
на многочлен ![]() .
.
-
Знайдіть суму коефіцієнтів многочлена, який утвориться після розкриття дужок та зведення подібних у виразі
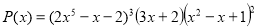 .
.
-
Знайдіть суму коефіцієнтів многочлена

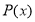 (див. № 2)
(див. № 2)
- при парних степенях змінної;
- при непарних степенях змінної.
- Задача (Відбір на ІVзаключний етап всеукраїнської математичної олімпіади, 2007-2008 н.р)
Назвемо многочлени ![]() і
і ![]() подібними, якщо вони мають однаковий степінь та однакові коефіцієнти, які, можливо, розташовані у різному порядку. Доведіть, що:
подібними, якщо вони мають однаковий степінь та однакові коефіцієнти, які, можливо, розташовані у різному порядку. Доведіть, що:
-
многочлен
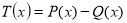 ділиться націло на
ділиться націло на 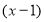 ;
;
-
число
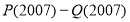 кратне
кратне  .
.
-
Чи існує деяке натуральне число
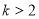 , що для будь-яких двох подібних многочленів
, що для будь-яких двох подібних многочленів 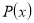 і
і 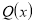 виконується умова:
виконується умова: 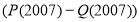
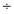
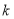 ?
?
-
Використовуючи теорему Безу та метод невизначених коефіцієнтів, розкласти на множники:
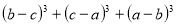 .
.
-
Доведіть, що многочлен
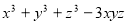 ділиться націло на многочлен
ділиться націло на многочлен 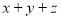 .
.
-
Доведіть, що число
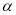 ірраціональне, якщо: 1)
ірраціональне, якщо: 1)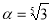 ; 2)
; 2)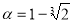 .
.
- Задача (ІІІ етап всеукраїнської математичної олімпіади,11 клас, 2008-2009 н.р)
Чи існує такий многочлен ![]()
![]() , усі три корені якого – цілі числа та
, усі три корені якого – цілі числа та ![]() - просте число?
- просте число?
- Задача (Збірник завдань для ДПА з математики, 11 клас, 2005 рік)
При яких раціональних значеннях параметрів ![]() і
і ![]() один з коренів многочлена
один з коренів многочлена ![]() дорівнює
дорівнює ![]() ?
?
-
Розв'яжіть систему рівнянь:
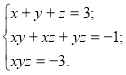
- Задача (Збірник завдань для ДПА з математики, 11 клас, 2005 рік)
При яких значеннях параметра ![]() многочлен
многочлен ![]() має три дійсних корені, які утворюють геометричну прогресію?
має три дійсних корені, які утворюють геометричну прогресію?
3. Задачі для домашньої роботи
- Використовуючи теорему Безу та метод невизначених коефіцієнтів, розкласти на множники:
1) ![]() ;
;
2) ![]() .
.
-
Доведіть, що число
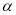 ірраціональне, якщо: 1)
ірраціональне, якщо: 1)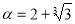 ; 2)
; 2)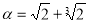 .
.
- Задача (Збірник завдань для ДПА з математики, 11 клас, 2005 рік)
При яких раціональних значеннях параметрів ![]() і
і ![]() один з коренів многочлена
один з коренів многочлена ![]() дорівнює
дорівнює ![]() ?
?
- Задача (Збірник завдань для ДПА з математики, 11 клас, 2005 рік)
При яких значеннях параметра ![]() многочлен
многочлен ![]() має три дійсних корені, які утворюють геометричну прогресію?
має три дійсних корені, які утворюють геометричну прогресію?
-
Розв'яжіть систему рівнянь:
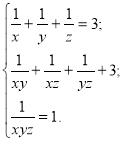
4. Відповіді та вказівки
-
Відповідь:
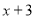
Розв’язання
Нехай при діленні многочлена ![]() на многочлен
на многочлен ![]() неповна частка дорівнює
неповна частка дорівнює ![]() , а остача -
, а остача - ![]() , тоді можна записати рівність:
, тоді можна записати рівність: ![]() . Оскільки степінь многочлена
. Оскільки степінь многочлена ![]() дорівнює 2, то степінь
дорівнює 2, то степінь ![]() не вище першої, тому многочлен має вид
не вище першої, тому многочлен має вид ![]() . За теоремою Безу
. За теоремою Безу ![]() ,
, ![]() . Отримаємо систему
. Отримаємо систему ![]() , розв’язавши яку знайдемо
, розв’язавши яку знайдемо ![]() .
.
-
Сума коефіцієнтів
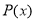 дорівнює
дорівнює 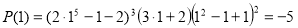 .
.
-
Сума коефіцієнтів
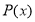 при парних степенях дорівнює
при парних степенях дорівнює 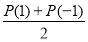 , при непарних степенях
, при непарних степенях 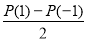 .
.
-
За умовою многочлени
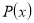 і
і 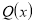 мають однаковий степінь та однакові коефіцієнти, які, можливо, розташовані у різному порядку, тому суми коефіцієнтів рівні і дорівнюють
мають однаковий степінь та однакові коефіцієнти, які, можливо, розташовані у різному порядку, тому суми коефіцієнтів рівні і дорівнюють 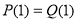 , тоді
, тоді 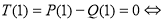
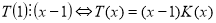 . При
. При 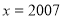
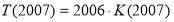
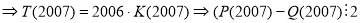 і
і 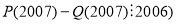 .
.
-
Відповідь:
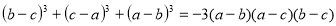
Розв’язання
Будемо вважати у многочлені ![]() одну з букв змінною, а інші – параметрами. Тоді многочлен
одну з букв змінною, а інші – параметрами. Тоді многочлен ![]() і
і ![]() , оскільки при
, оскільки при ![]()
![]() і при
і при ![]()
![]() . Міркуючи аналогічно, многочлен
. Міркуючи аналогічно, многочлен ![]() , бо при
, бо при ![]()
![]() . Тоді многочлен
. Тоді многочлен ![]() ділиться націло на добуток
ділиться націло на добуток ![]() . Оскільки степінь діленого та степінь дільника рівні, то частка є многочлен нульового степеня, тобто – число( позначимо його
. Оскільки степінь діленого та степінь дільника рівні, то частка є многочлен нульового степеня, тобто – число( позначимо його ![]() ).
).
Маємо рівність ![]()
![]() . При
. При ![]() отримаємо
отримаємо ![]() , звідси
, звідси ![]() ,
, ![]()
-
Достатньо розглянути многочлен
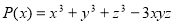 та показати, що
та показати, що 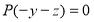 .
.
-
Для доведення складемо многочлен з цілими коефіцієнтами , корінь якого дорівнює
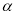 і який не має раціональних коренів.
і який не має раціональних коренів.
1)Нехай ![]() - корінь
- корінь ![]() . Найпростіший многочлен, для якого
. Найпростіший многочлен, для якого ![]() - корінь є многочлен
- корінь є многочлен ![]() . З означення кореня маємо
. З означення кореня маємо ![]()
![]() . Очевидно, що многочлен
. Очевидно, що многочлен ![]() не має раціональних коренів. Оскільки,
не має раціональних коренів. Оскільки, ![]() - корінь, то число
- корінь, то число ![]() - ірраціональне
- ірраціональне
2) міркування аналогічні.
- Відповідь: не існує.
Розв'язання
Нехай ![]() - цілі корені многочлена
- цілі корені многочлена![]()
![]() , та
, та ![]() - просте число. Тоді
- просте число. Тоді ![]()
![]() . Звідси
. Звідси ![]() і
і ![]() - просте число, тому без втрати загальності можна вважати, що
- просте число, тому без втрати загальності можна вважати, що ![]() і
і ![]() . Розв’язуючи рівняння отримуємо, що
. Розв’язуючи рівняння отримуємо, що ![]() і
і ![]() . При
. При ![]()
![]() , тоді
, тоді ![]() . Перевіркою встановлюємо, що тоді число
. Перевіркою встановлюємо, що тоді число ![]() не є простим. При інших значеннях
не є простим. При інших значеннях ![]() і
і ![]() цілих значень
цілих значень ![]() не існує.
не існує.
-
Відповідь:
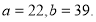
Розв'язання
![]() - корінь многочлена
- корінь многочлена ![]() , тому з означення кореня випливає, що правильна рівність
, тому з означення кореня випливає, що правильна рівність ![]() Розкриємо дужки та зведемо подібні доданки у лівій частині рівняння:
Розкриємо дужки та зведемо подібні доданки у лівій частині рівняння:
![]() (*). За умовою значення параметрів
(*). За умовою значення параметрів ![]() і
і ![]() є раціональними числами, тому раціональними будуть значення виразів
є раціональними числами, тому раціональними будуть значення виразів ![]() і
і ![]() , але
, але ![]() - ірраціональне, тому рівність (*) має місце лише тоді, коли виконується система
- ірраціональне, тому рівність (*) має місце лише тоді, коли виконується система ![]() Звідки
Звідки ![]()
![]()
-
Відповідь:
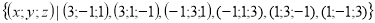
Розв'язання
Скористаємось, теоремою, оберненою до теореми Вієта, для зведеного многочлена третього степеня, тоді ![]() - корені рівняння
- корені рівняння ![]() , розв’язуючи яке, знаходимо
, розв’язуючи яке, знаходимо ![]() . Розв’язком системи є впорядкована трійка чисел
. Розв’язком системи є впорядкована трійка чисел ![]() . Враховуючи порядок, записуємо розв'язки системи.
. Враховуючи порядок, записуємо розв'язки системи.
-
Відповідь:
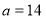
Розв'язання
Нехай корені многочлена![]() утворюють геометричну прогресію , перший член якої дорівнює
утворюють геометричну прогресію , перший член якої дорівнює ![]() , а знаменник дорівнює
, а знаменник дорівнює ![]() , тоді їх можна записати як
, тоді їх можна записати як ![]() . Застосовуючи теорему Вієта, отримаємо систему рівнянь
. Застосовуючи теорему Вієта, отримаємо систему рівнянь ![]()
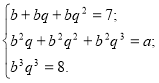 Звідси
Звідси ![]()
![]() .
.
Список використаних джерел
- Ковтонюк М.М. Алгебра та початки аналізу. 10 клас / М.М.Ковтонюк, В.А. Ясінський, С.М. Бак. – Х.: Вид. група «Основа», 2005
- Математичні олімпіадні змагання школярів України 2007—2008 та 2008—2009. Анікушин А.В., Арман А.Р. та ін. За ред. Рубльова Б.В. – Львів: Каменяр, 2010 – 552с
- Мерзляк А.Г. Алгебра та початки аналізу: підруч. для 10 кл. загально освіт. навч. закладів: проф. рівень / А.Г. Мерзляк, Д.А.Номіровський, В.Б.Полонський, М.С. Якір. – Х.: Гімназія, 2010
- ШкільМ.І., Колесник Т.В., Хмара Т.М. Алгебра і початки аналізу : підруч. для 10 кл. з поглибл. вивч. математики в середніх закладах освіти. – К.: Освіта, 2004
- Збірник завдань для ДПА з математики для 11 кл. : - Х., Генеза, 2005 рік


про публікацію авторської розробки
Додати розробку
