Урок на тему "Теорема Вієта"

Девіз: „Вивчіть «ази» науки, перш ніж зійти на її вершину, ніколи не     беріться за вивчення наступного, не засвоївши попереднього.”

                                                                                                          І.П.Павлов

Тема. Зведене квадратне рівняння. Теорема Вієта.

Мета. Закріпити поняття зведеного квадратного рівняння; теореми Вієта  оберненої Теореми Вієта та наслідків з них. Формувати вміння застосовувати теорему при розв’язуванні квадратних рівнянь, знаходити суму та добуток коренів зведеного квадратного рівняння, здатність робити висновки. Знайти закономірність між коефіцієнтами зведеного квадратного рівняння і коренями, що дорівнюють 1 або -1. Розвивати логічне мислення, самостійність та вміння узагальнювати вивчені факти. Виховувати наполегливість, інтерес до математики.

Учні повинні:  мати уявлення про зведене квадратне рівняння;

  уміти знаходити суму та добуток коренів зведеного                квадратного рівняння, визначати знаки коренів та знаходити його корені за допомогою оберненої теореми Вієта.

Тип уроку. Урок засвоєння нових знань.

Обладнання: картки із завданнями для індивідуальної роботи, мультимедійна презентація.

 

 

1. Актуалізація опорних знань учнів.

Завдання 1. Проводиться у формі фронтального опитування як інтерактивна вправа „Мікрофон”.

1. Які види рівнянь ви знаєте?
2. Сформулюйте означення повного квадратного рівняння.
3. Чи має “обмеження” квадратне рівняння стосовно своїх коефіцієнтів? Якщо так, то чому?
4. Скільки коренів має повне квадратне рівняння?
5. Як називаються квадратні рівняння, в яких другий коефіцієнт та вільний член можуть дорівнювати нулю?
6.  Навести приклади неповних квадратних рівнянь.
7.  Дайте означення неповного квадратного рівняння.
8.  Як називаються в повному квадратному рівнянні числа а, b, с?
9.  Скільки коренів має рівняння виду ах² = 0?
10.  Наведіть приклад квадратного рівняння виду ах² + bх = 0. Сформулюйте алгоритм розв’язування цього виду рівняння.
11.  Чи має розв’язки рівняння 2х² + 8 = 0?Чому?
12.  Сформулюйте алгоритм розв’язування рівняння виду ах² + с = 0.В якому випадку таку квадратне рівняння буде мати корені?
13. Сконструюйте квадратне рівняння, в якого старший коефіцієнт дорівнює 3, другий – 5, а вільний член дорівнює 0.
14. Наведіть приклад квадратного рівняння, у якого другий коефіцієнт і вільний член дорівнюють –2.
15.  Сконструюйте і розв’яжіть неповне квадратне рівняння, у якого старший коефіцієнт дорівнює –5, вільний член дорівнює 7.
16.  Скільки існує способів розв’язування повних квадратних рівнянь? Назвіть їх.
17.  Що таке дискримінант квадратного рівняння?
18.  Який зв’язок існує між дискримінантом і коренями квадратного рівняння?
19.  Назвіть формулу коренів квадратного рівняння, у випадку якщо дискримінант додатній.
20.  Якого виду набуває ця формула, якщо дискримінант дорівнює нулю?
21.  Що можна сказати про корені квадратного рівняння, якщо дискримінант від’ємний?
22.   Як називається квадратне рівняння, в якого старший коефіцієнт дорівнює одиниці?
23.  Яку ви знаєте залежність між коренями зведеного квадратного рівняння і його коефіцієнтами?
24. Сформулюйте теорему Вієта.
25. Сформулюйте обернену теорему Вієта.
26.  Який наслідок з теореми Вієта вам відомий. Для яких рівнянь він використовується?

 

 

Завдання 2 . Заповніть таблицю і визначіть корені квадратного рівняння.

		с		- b
І
ІІ
ІІІ
ІV

Запитання: Якою теоремою чи наслідком користувалися при виконанні цього завдання? Сформулюйте це твердження.

Завдання 3. Заповніть таблицю і складіть зведене квадратне рівняння, якщо:

					Зведене квадратне рівняння
І	4	-3
ІІ	5	2
ІІІ	-3	-6
ІV	8	12

Запитання: Яка теорема прийшла на допомогу в цьому випадку? Сформулюйте її.

Робота в групах.

Алгоритм роботи над завданням:

1. Розв’яжіть рівняння  в зошиті згідно вашого номера.
2. Зробіть взаємоперевірку.
3. Упорядкуйте корені вашого рівняння так, щоб
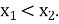
4. Утворіть координати точок (х; у) так, щоб , 
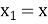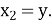
5. У відповідній послідовності (послідовність нанесення точок відповідає номерам рівнянь) позначте отримані точки на координатній площині і послідовно з’єднайте їх відрізками.
6. Ви отримаєте рисунок.

	І група	ІІ група	ІІІ група	ІV група
1.
2.
3.
4.
5.
6.

• Продемонструйте свої малюнки.
• Отож, у нас утворилося число 2003. Чому саме 2003 і що воно означає скажете ви?
• Ви займалися розшифровкою, або ще кажуть дешифруванням.
• Сьогодні на календарі 14 квітня. І саме цього дня 2003 року завершився наймасштабніший  науковий проект в історії людства, під назвою “Геном людини”. 14 квітня було оголошено про повну розшифровку генома людини.  Проект тривав 15 років. У проекті на різних етапах були зайняті тисячі фахівців із усього світу: біологи, хіміки, математики, фізики, програмісти й техніки. Як наслідок виникла навіть нова галузь науки – біоінформатика. Це один з найдорожчих наукових проектів в історії. Тільки за період з 1990 по 1998 р. на нього було витрачено більше $1,5 млрд. 
• Що ви розумієте під “геномом людини”?

 

 

• ГЕНОМ людини науковці вважають  сукупність всіх генів і міжгенних ділянок ДНК. За оцінками, він складається з 20-25 тис. генів.
• Іншими словами геном - генетична програма живого організму. Будь-яке порушення ("збій") цієї програми, веде до мутацій. З 10 тис. відомих захворювань людини близько 3 тис. - спадкові хвороби. Розшифрування геному людини дозволить боротися з цими хворобами і вселяє надію міліонам людей планети на здорове життя.

• Як демонструє цей проект: - тільки злагоджена і спільна робота веде до омріяних результатів.
• Кожна висока наука починається з шкільної парти. Пропоную вам теж провести ряд досліджень нашої теми.
• Повернемося до нашого попереднього завдання. Якщо уважно подивитися на корені цих рівнянь, то серед них часто зустрічаються 1 чи -1.
• Виникає запитання: чи існує якась закономірність між коефіцієнтами і коренями х=1 та х=-1?

-проблема: коли зведене квадратне рівняння має корінь 1 або –1?

-  Назвіть номери кожної групи рівнянь, в яких один із коренів 1 або -1.

- Дослідимо їх класифікуючи їх у дві групи. До першої групи віднесемо рівняння, одним із коренів якого є 1, а другу групу – 1.  Уважно подивіться на їх коефіцієнти. Чи помітили ви якусь закономірність?

І група: один із коренів дорівнює 1		ІІ група: один із коренів дорівнює -1
1;  3		-1;  2
1;  2		-1;  5
1;  5		-1;  4
1 ; -3		-1;  6
1;  -2		-1;  -3

 

- Чи помітили ви іншу закономірність відносно другого кореня рівнянь?

• Сформулюйте загальний висновок щодо закономірностей, які ви помітили?

Демонструється таблиця,  інформацію  з якої учні переписують в зошити.

Для зведеного квадратного рівняння х2 + bx + c = 0
Якщо
a +  c = - b, то х1 = 1,  х2 = с;	a  + c =  b,       то х1 = – 1,  х2 = - с.

• Перевіримо наше твердження для наступних рівнянь.

Завдання 6.

	Рівняння	Корені
І група
ІІ група
ІІІ група
ІV група

• Як ви гадаєте що дає нам знання цієї закономірності?
• Напрошується природнє запитання: “Чи існує подібна закономірність і для незведених квадратних рівнянь?”.
• Пропоную над цим завданням подумати вдома і результати своїх міркувань оформити у вигляді міні проекту та продемонструвати нам на наступному уроці.

Завдання 7. Один з коренів квадратного рівняння   дорівнює 1. Знайдіть і другий корінь.

- Скількома способами можна це зробити?

(Робота біля дошки)

№ 671 (з підручника). Скількома способами можна вирішити це завдання? Чому?

(Робота біля дошки)

- Пропоную вашій увазі завдання, які взяті із тренувальних збірників для підготовки до ДПА та ЗНО.

Завдання 1-4 мають п’ять варіантів відповідей, серед яких лише ОДИН ПРАВИЛЬНИЙ. Виберіть правильну, на вашу думку, відповідь і позначте її. 

8. Знайдіть суму коренів рівняння  х² – 10х + 25 = 0.

А	Б	В	Г	Д
5	−10	−5 і 5	10	−5

9. Для якого з наведених рівнянь сума його дійсних коренів дорівнює 5?

А	Б	В	Г	Д

10.  Для якого з наведених рівнянь добуток  його дійсних коренів дорівнює 3?

А	Б	В	Г	Д

 

11. Укажіть правильні твердження.

А Сума коренів квадратного рівняння  х² – 5х – 8 = 0 дорівнює - 5.

Б Добуток коренів квадратного рівняння х² + 3х – 7 = 0 дорівнює 7.

В Один із коренів квадратного рівняння дорівнює 1.

Г У квадратному рівнянні х² – 5х + 6 = 0 сума коренів дорівнює 5, а добуток – 6.

Д Один із коренів квадратного рівняння дорівнює -1.

Завдання на встановлення відповідності.

12. Установіть відповідність між рівняннями (1 − 4) та їх коренями (А – Д).

1.   х2 – х – 6 = 0	А. −3; −2
2.   х2 – 5х + 6 = 0	Б. −2; 3
3.   х2 + х – 6 = 0	В. 2; 3
4.  х2 + 5х + 6 = 0	Г. Коренів немає
	Д. −3; 2

 

Завдання відкритої форми.

13.Знайдіть р і х₁, якщо  х²  + px + 28 = 0 і х₂ = − 7, де х₁ і х₂ – корені квадратного рівняння.

Підсумок уроку.

Продовжіть речення:

Сьогодні на уроці я:

Повторив …..

Закріпив ….

Дізнався …

Вивчив ….

Зрозумів ….

Засвоїв ….

Домашнє завдання.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

І     ГРУПА

Завдання 4. Робота в групах.

Алгоритм роботи над завданням:

1.Розв’яжіть рівняння  в зошиті згідно вашого номера.

2.Зробіть взаємоперевірку.

3.Упорядкуйте корені вашого рівняння так, щоб

4.Утворіть координати точок (х; у) так, щоб , 

5.У відповідній послідовності (послідовність нанесення точок відповідає номерам рівнянь) позначте отримані точки на координатній площині і послідовно з’єднайте їх відрізками.

6.Ви отримаєте рисунок.

	І група
1.
2.
3.
4.
5.
6.

 

 

 

 

 

 

 

 

 

 

 

 

 

ІІ     ГРУПА

Завдання 4. Робота в групах.

Алгоритм роботи над завданням:

1. Розв’яжіть рівняння  в зошиті згідно вашого номера.
2. Зробіть взаємоперевірку.
3. Упорядкуйте корені вашого рівняння так, щоб
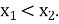
4. Утворіть координати точок (х; у) так, щоб , 
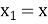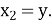
5. У відповідній послідовності (послідовність нанесення точок відповідає номерам рівнянь) позначте отримані точки на координатній площині і послідовно з’єднайте їх відрізками.
6. Ви отримаєте рисунок.

 

 

	ІІ група
1.
2.
3.
4.
5.
6.

 

 

 

 

 

 

 

 

ІІІ     ГРУПА

Завдання 4. Робота в групах.

Алгоритм роботи над завданням:

1.Розв’яжіть рівняння  в зошиті згідно вашого номера.

2.Зробіть взаємоперевірку.

3.Упорядкуйте корені вашого рівняння так, щоб

4.Утворіть координати точок (х; у) так, щоб , 

5.У відповідній послідовності (послідовність нанесення точок відповідає номерам рівнянь) позначте отримані точки на координатній площині і послідовно з’єднайте їх відрізками.

6.Ви отримаєте рисунок.

 

 

	ІІІ група
1.
2.
3.
4.
5.
6.

 

 

 

 

 

 

 

 

ІV    ГРУПА

Завдання 4. Робота в групах.

Алгоритм роботи над завданням:

1.Розв’яжіть рівняння  в зошиті згідно вашого номера.

2.Зробіть взаємоперевірку.

3.Упорядкуйте корені вашого рівняння так, щоб

4.Утворіть координати точок (х; у) так, щоб , 

5.У відповідній послідовності (послідовність нанесення точок відповідає номерам рівнянь) позначте отримані точки на координатній площині і послідовно з’єднайте їх відрізками.

6.Ви отримаєте рисунок.

	ІV група
1.
2.
3.
4.
5.
6.

 

 

 

 

 

 

 

 

 

Листок довіри групи І

Прізвище учня   Завдання


 

 

 

Листок довіри групи ІІ

Прізвище учня   Завдання


 

 

 

Листок довіри групи ІІІ

Прізвище учня   Завдання


 

 

 

Листок довіри групи ІV

Прізвище учня   Завдання


 

Для зведеного квадратного рівняння  х2 + bx + c = 0
Якщо
a +  c = - b, то х1 = 1, х2 = с;	a  + c =  b, то  х1 = – 1, х2 = - с.

 

 

РЕЗЕРВНІ ЗАВДАННЯ:

Завдання 1-6 мають п’ять варіантів відповідей, серед яких лише ОДИН ПРАВИЛЬНИЙ. Виберіть правильну, на вашу думку, відповідь і позначте її.  Кожне завдання 1-6 оцінюється одним балом.

• 1. Визначити яке з рівнянь є квадратним?

А	Б	В	Г	Д
х2 + 5х – 8 = 0	−6 (2х – 9) = 0		х – 9 = 0

 

• 2. Знайдіть дискримінант квадратного рівняння  3х² + 4х – 5 = 0.

А	Б	В	Г	Д
−71	76	73	−76	81

 

• 3. Складіть квадратне рівняння, коефіцієнти якого дорівнюють: а = 2,
• b = −5, с = 8.

А	Б	В	Г	Д
5х2 −8х +2= 0	8х2 −5х +2= 0	2х2 −5х +8= 0	2х2 −8х +5= 0	5х2 +2х –8= 0

 

• 4. Зведіть рівняння  (х + 3)(х – 3) = 2х − 4  до вигляду ах² + bх + с = 0.

А	Б	В	Г	Д
−х2 + 13х  = 0	х2 +2х +13= 0	х2 +2х –13= 0	х2 −2х –5 = 0	х2 −2х +13= 0

 

• 5. Розв’яжіть рівняння  6х² = −24.

А	Б	В	Г	Д
−2 і 2	−4	−2	2	Коренів немає

 

• 6. Знайдіть суму коренів рівняння  х² + 10х + 25 = 0.

А	Б	В	Г	Д
−5	−10	0	10	5

 

Завдання з вибором кількох правильних відповідей. Завдання оцінюється двома балами.

• 7. Укажіть правильні твердження.

1. Сума коренів квадратного рівняння 2х² – 7х – 8 = 0 дорівнює 3,3.
2. Добуток коренів квадратного рівняння х² + 3х + 7 = 0 дорівнює 7.
3. Дискримінант квадратного рівняння 0,5х² + 4х + 3 = 0 дорівнює 10.
4. Рівняння 5х² + 2х + 1 = 0 має два корені.
5. Коефіцієнти квадратного рівняння 2х² − 7х + 13 = 0 дорівнюють: а = 2, b = −7, с = 13.
6. Рівняння 2х² − 9х − 4 = 0 не має коренів.
7. У квадратному рівнянні  х² – 6х +5 = 0 сума коренів дорівнює 6, а добуток – 5.

Завдання на встановлення відповідності. Завдання оцінюється двома балами.

• 8. Установіть відповідність між рівняннями (1 − 4) та їх коренями (А – Д).

1.   х2 + х – 6 = 0	А. 2; 3
2.   х2 + 5х + 6 = 0	Б. −3; 2
3.   х2 − х – 6 = 0	В.  −3; −2
4.  х2 − 5х + 6 = 0	Г. Коренів немає
	Д. −2; 3

 

Завдання відкритої форми з розгорнутою відповіддю. Кожне завдання 9 – 10 оцінюється одним балом.

• 9. Розв’яжіть рівняння (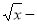1)(х² + 14х – 15)  = 0.
• 10. Знайдіть q і х₂, якщо х²  + qx + 35 = 0 і х₁ = 5, де х₁ і х₂ – корені квадратного рівняння.