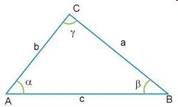
Урок на тему: "Теореми синусів і косинусів. Практичні задачі"

Урок з геометрії в 9-му класі.

Розроблено та проведено 

вчителем математики ЗОШ № 7 ім. В. В. Бражевського м. Житомира

Сергієм Олександровичем Сафонюком

Завдання уроку:  1) розв’язати прикладні задачі, підготовлені учнями;

                             2) скласти умову прикладної задачі за рисунками, які подані в підручнику та розв’зати їх. 

Обладнання: мультимедійне устаткування, електронні носії інформації, дошка, зошити,                          креслярські інструменти.

          Як можна визначити своє місцезнаходження на місцевості,             як знайти відстань до неприступного предмету? Це питання стояло ще в давнину перед людьми. З історії відомо, що мандрівники та корабели h орієнтувалися за зірками і планетами, причому могли досить точно визначити своє                                               орієнтирів для них була висота,місцезнаходження. Одним із                                                                                                                  

                                    A _B на яку піднімалось відоме їм                                                                                                       світило в даній місцевості на даний момент часу. Але виміряти цю висоту безпосередньо зрозуміло було неможливо. Тому суттєву роль відігравало вміння розв’язувати трикутник з двома вершинами на поверхні  Землі, а третьою - слугувало небесне світило.  

Задача 1. Як знайти висоту Сонця, якщо його з місця  А  видно під кутом , з місця В під кутом , а відстань між А і В дорівнює а?

  В давнину для цього використовували сонячний годинник або астролябію. До речі, учення про сонячний годинник (гномоніка) ввели арабські вчені. Спочатку розберемось, що означає вираз « видно під кутом»?  Якщо провести уявний перпендикуляр від  Сонця до Землі та уявну похилу від нього до місця перебування спостерігача, то кут між похилою і її проекцією (тінню) і буде тим кутом, під яким видно, наприклад, Сонце.

  Щоб розв’язати цю задачу  згадаємо теореми та формули, які дозволяють це зробити. 

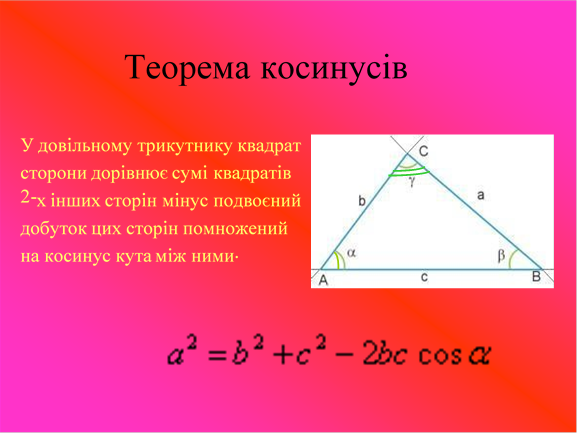
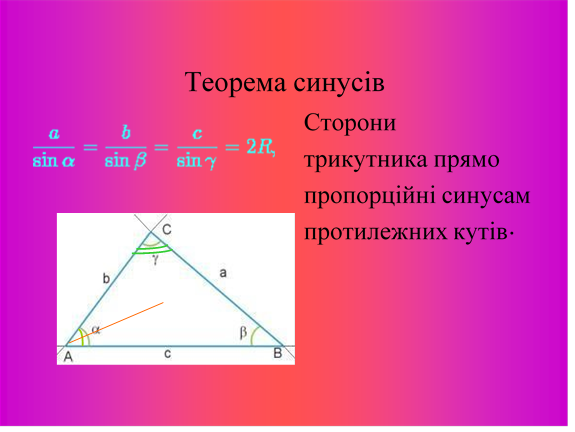
В наш час, використовуючи ці теореми розв’язати проблему задачі № 1 можна швидше та точніше.

           Тепер згадаємо як можна знаходити невідомі величини в даних теоремах.

Розв’язування задачі № 1

                                                                   Дано: САК =, СКВ =, АК = а

С                          Знайти: СВ

 Розв’язання.

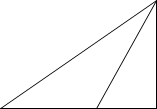Примітка: перш ніж перейти до розв’язку задачі  учням можна                                      нагадати, що існує іноді декілька способів  розв’язування задач. Тому розглянемо хоча б 2 способи. 

1  спосіб.

                 Розглянемо  АСК В ньому САК =, АКС =, А                   К                В де =180⁰- ( і  - суміжні кути), АК = а. 

АСК= 180⁰-(+)= 180⁰--180⁰+=-. За теоремою синусів маємо

         AK                AC            AC  AK sinAKC  asin180⁰ _  asin . Розглянемо 

                                             

sinACK sinAKC                             sinACK             sin    sin

АСВ. (_В=90⁰). CB  AC sinA _ asin^sin^. sin

2  спосіб.

Розглянемо  АСК В ньому САК =, АКС =, де =180⁰- ( і  - суміжні кути), АК = а. АСК= 180⁰-(+)= 180⁰--180⁰+=-. За теоремою синусів маємо:

         AK              CK            CK  AK sinCAK  asin                                               0).

. Розглянемо КСВ. (В=90 sinACK sinCAK         sinACK         sin

CB  CK sinBKC  asin^sin^ . Як бачимо, ми отримали однакові результати. sin

 За домовленістю вирішено, що в довільному трикутнику зі сторонами AB (c), BC (a), AC (b) протилежні кути відповідно позначають α, β, γ.    Задача 2

Розв’язання

Δ АВС За теоремою синусів маємо:

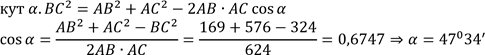
За теоремою синусів знайдемо, наприклад, кут       .

Відомо, 𝛼 + 𝛽 + 𝛾 = 180⁰ ⇒ 𝛽 = 180⁰ − 47⁰34^′ − 32⁰14^′ = 100⁰12^′

Відповідь: 47⁰34^′; 32⁰14^′; 100⁰12^′.

Примітка: після розв’язання задач учням було вказано на те, що грані пірамід були рівнобедреними або рівносторонніми трикутниками.

Задача 4.  

При розв’язуванні задач практичного змісту доцільно створити математичну модель.

А                                          В Дано: ∆ АВС

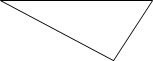АС = 93 м, АВ = 65 м, ∠𝐵𝐴𝐶 = 42⁰

Знайти: ВС 

                                   С Розв’язання

                                                    ∆ АВС.   За теоремою косинусів знайдемо сторону ВС.

𝐵𝐶² = 𝐴𝐶² + 𝐴𝐵² − 2 ∙ 𝐴𝐶 ∙ 𝐴𝐵 ∙ cos ∠𝐵𝐴𝐶

𝐵𝐶² = 93² + 65² − 2 ∙ 93 ∙ 65 ∙ cos 42⁰ =

= 8649 + 4225 − 8982,87 = 3891,13 ⇒ 𝐵𝐶 ≈ 62 (м)

Відповідь: 62 м

Задача 5.

Розв’яжемо дану задачу двома способами: за теоремою косинусів і через співвідношення у прямокутному трикутнику, та порівняємо отримані результати.

Спосіб 1.                             В Дано: ∆ АВС – рівнобедрений

АВ = ВС = 10 м

∠𝐴𝐵𝐶 = 120⁰

                     А                                               С        Знайти: АС

Розв’язання

                                                  ∆ АВС. За теоремою косинусів знайдемо сторону АС.

                                                  𝐴𝐶² = 𝐵𝐶² + 𝐴𝐵² − 2 ∙ 𝐵𝐶 ∙ 𝐴𝐵 ∙ cos ∠𝐴𝐵𝐶

𝐴𝐶 = √10² + 10² + 2 ∙ 10 ∙ 10 ∙ 0,5 = √300 = 10√3 ≈ 17,3 (м)

Врахували,що cos 120⁰ = − cos 60⁰ = −0,5

Відповідь: 17,3 м

Спосіб 2.

                           В Дано: ∆ АВС – рівнобедрений

АВ = ВС = 10 м

∠𝐴𝐵𝐶 = 120⁰

    А                                                С ВК - висота 

                             К Знайти: АС

Розв’язання

У ∆ АВС АВ = ВС, тому висота ВК є також медіаною та                                                     бісектрисою. Отже АК = КС, ∠𝐴𝐵𝐾 = ∠𝐶𝐵𝐾 = 60⁰ ∆ ABK (∠𝐴𝐾𝐵 = 90⁰). ∠𝐴𝐵𝐾 = 60⁰ ⇒ ∠𝐵𝐴𝐾 = 30⁰ ⇒

). За теоремою Піфагора маємо

                                                   .

Отже, АС = 10√3 ≈ 17,3 (м).

              Висновок можна зробити наступний: кожний спосіб розв’язування                                                задач має право на існування.                                                 Відповідь:   10√3 ≈ 17,3 (м).

В давнину для вимірювання кутів використовували прилад,  який мав назву – астролябія.  На уроках геометрії учні  використовують транспортир. Для вимірювання кутів на  місцевості використовують теодоліт.

Задачі, які мають практичне значення

В сучасному житті для розв’язання прикладних задач треба вміти побудувати математичну  ( в нашому випадку – геометричну ) модель задачі, правильно вибрати формули та вірно їх застосувати, причому в деяких задачах декілька раз.

Задача 6.

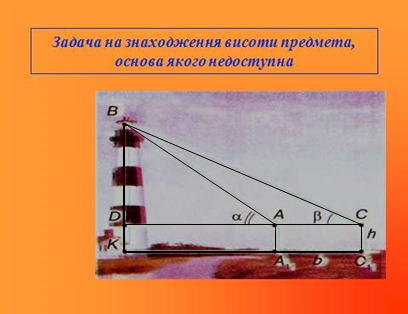
Знайти висоту маяка, підхід до  якого перегороджує річка. На практиці це виконують так:

відмічають дві точки на  горизонтальній прямій, яка проходить через основу маяка; в кожній точці за допомогою теодоліта визначають кут, під яким видно верхівку об’єкта; проводять відповідні обчислення. Складемо умову даної задачі, зробимо рисунок та проведемо розрахунки.

З двох точок А і С, відстань між якими 12 м, вершину маяка  видно під кутами 42⁰ та 37⁰ відповідно. Висота приладу над землею – h = 1,5 м. Знайти висоту маяка.

     В Дано: ΔАВС

∠𝐵𝐶𝐴 = 37⁰, ∠𝐵𝐴𝐷 = 42⁰

AC = 12 м, AA₁ = CC₁ = h = 1,5 м

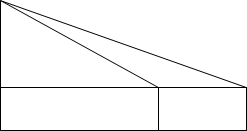Знайти: КВ     D                                         A C

K                                   A₁                  C₁

Розв’язання

Δ𝐴𝐵𝐶: ∠𝐵𝐶𝐴 = 37⁰, ∠𝐵𝐴𝐷 = 42⁰ ⇒ ∠𝐴𝐵𝐶 = 42⁰ − 37⁰ = 5⁰ (властивість зовнішнього кута).

За теоремою синусів маємо:  

Δ BDA (∠𝐷 = 90⁰). 𝐵𝐷 = 𝐴𝐵 ∙ sin ∠𝐵𝐴𝐷 = 82,8 ∙ sin 42⁰ = 82,8 ∙ 0,6691 = 55,4 (м). ВК = BD + DK = 55,4 + 1,5 ≈ 57 (м).

Відповідь: 57 м

Задача 7.

На горі знаходиться маяк висотою 60 м. Перший спостерігач на даху  бачить біля підніжжя гори деякий  предмет під кутом 65⁰, а другий,  який знаходиться на вершині гори,  бачить його під кутом 35⁰. Яка висота гори?

Задача, яка вимагає побудови геометричної моделі, вміння вибрати та застосувати певні формули.

Зробимо рисунок до задачі та  складемо скорочений запис умови.

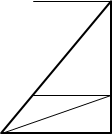
                     М В

Дано: ∆ 𝐴𝐵𝐷 (∠𝐴𝐷𝐵 = 90⁰)

𝐵𝑀 ∥ 𝐶𝐾 ∥ 𝐴𝐷

                  K                      C          Знайти: СВ

                                                                     Розв’язання А                             D

1.   

2.  ∆𝐴𝐶𝐵. За теоремою синусів   

0

                                                        AC

3.  ∆𝐴𝐶𝐷 (∠𝐴𝐷𝐶 = 90⁰), ∠𝐴𝐶𝐷 = 180⁰ − ∠𝐾𝐶𝐴 − ∠𝐾𝐶𝐵

∠𝐴𝐶𝐷 = 180⁰ − 35⁰ − 90⁰ = 55⁰

𝐶𝐷 = 𝐴𝐶 cos 55⁰ = 50,7 ∙ 0,5736 ≈ 29,1(м) Відповідь: 29,1 м

Задача 8.

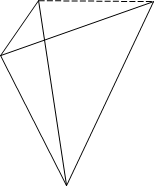
                C                              D Дано:  АВ = 100 м

Знайти: CD

      A              O Розв’язок

                    1.  ∆𝐴𝐷𝐵. ∠𝐵𝐷𝐴 = 180⁰ − ∠𝐷𝐴𝐵 − ∠𝐴𝐵𝐶 − ∠𝐶𝐵𝐷 ∠𝐵𝐷𝐴 = 180⁰ − 70⁰ − 28⁰ − 54⁰ = 28⁰

 За теоремою синусів:    

0

                            В 2. ∆𝐴𝐶𝐵. ∠𝐵𝐶𝐴 = 180⁰ − ∠𝐶𝐴𝐷 − ∠𝐴𝐵𝐶 − ∠𝐷𝐴𝐵 ∠𝐵𝐶𝐴 = 180⁰ − 30⁰ − 28⁰ − 70⁰ = 52⁰

                                                                                                                                           𝐴𝐵                         𝐶𝐵

За теоремою синусів: 

0

3. ∆𝐶𝐵𝐷. 𝐶𝐵 = 125 м, 𝐷𝐵 = 200,1 м, ∠𝐶𝐵𝐷 = 54⁰                                                               За теоремою косинусів:

𝐶𝐷² = 𝐶𝐵² + 𝐷𝐵² − 2 ∙ 𝐶𝐵 ∙ 𝐷𝐵 ∙ cos ∠𝐶𝐵𝐷 𝐶𝐷 = √125² + 200,1² − 2 ∙ 100 ∙ 200,1 ∙ cos 54⁰=

                                                             = √15625 + 40040,01 − 23523,756 ≈ 179,3 (м).

Відповідь: 179,3 м

Примітка: як бачимо, в даній задачі використовували і теорему синусів, і теорему косинусів.      

Домашнє завдання

За готовими слайдами розв’язати задачі.

Фотографії з уроку