Урок "Найбільше і найменше значення функції."

                   Алгебра і початки аналізу 10 клас

          Тема уроку. Найбільше і найменше значення функції

.
 

(За підручником  Математика, А.Г. Мерзляк. — Х. : Гімназія, 2018)

 Підготувала

                                                                                         вчитель математики

                                                                                    Жадан

                                                                                      Людмила Миколаївна

Урок № 

Дата
Тема уроку. Найбільше і найменше значення функції.
Мета уроку. Навчити учнів застосовувати поняття похідної для знаходження найбільшого і найменшого значення функції на відрізку; застосовувати дані знання для розв’язування прикладних задач; розвивати логічне мислення, вміння аналізувати і узагальнювати; виховувати любов до предмету.

Тип уроку: формування знань і вмінь.

Епіграф уроку.         «Просто передати знання людині неможливо. Оволодіти ними      людина може шляхом власної діяльності».

                                 « Наповнити»  розум не можна, він сам повинен  усе засвоїти.»

                                                                                         А. Дістеверг
Хід уроку

І. Організаційна частина.

ІІ. Актуалізація опорних знань.

Запитання до учнів:

Що називають похідною функції?
Що називають диференціюванням?
Чому дорівнюють: похідні сталої,  x, kx, kx +b, xn , ,  , sinx, cosx?
Які точки називають критичними точками?
За якої умови функція зростає на деякому проміжку?
За якої умови функція спадає на деякому проміжку?
Що таке точки максимуму функції? Мінімуму?
Що  таке точки екстремуму?
Що означає дослідити функцію?

Завдання ЗНО:  

Встановити відповідність між функцією та її похідною

Відповіді: №3: 1-Б, 2-Д, 3-Г, 4-А.   №4: 1-Б, 2-В, 3-Д, 4-А.

ІІ. Мотивація навчальної діяльності.

• Людині у своїй діяльності часто доводиться вирішувати завдання, коли потрібно затратити якомога менше часу, сил, коштів для одержання найкращого результату. Наприклад, яких розмірів має бути ящик, щоб об’єм був найбільшим з вказаного матеріалу?
• Як зробити так, щоб деталі космічного корабля мали меншу масу? В якому місці побудувати міст через річку, щоб дорога була коротшою?
• Задачі такого типу називаються задачами на оптимізацію (від лат. Optimum – найкращий).
• Одна із стародавніх задач – задача Дідони, теж належить до задач на оптимізацію. Згідно легенди, Дідона – цариця Карфагену могла отримати тільки ту ділянку землі, яку обмежить шкіра вола. Цариця порізала шкіру вола на смужки і розклала їх так, що обмежена ділянка землі стала значно більшою, в порівнянні з тією, яку ю могла обмежити вся шкіра.

Задача по оповіданню Л. Толстого «Чи багато людині землі потрібно»

ІІІ. Пояснення нового матеріалу.
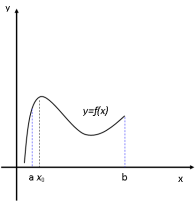
У випадку, коли функція є неперервною і має скінчену кількість стаціонарних точок ситуація змінюється, наприклад, стаціонарні точки х₁, х₂ розбивають відрізок [a,b] на менші відрізки, в середині яких стаціонарних точок немає.
Теорема: Якщо Функція f(x) неперервна на [a,b], то вона має на цьому відрізку найбільше і найменше значення.

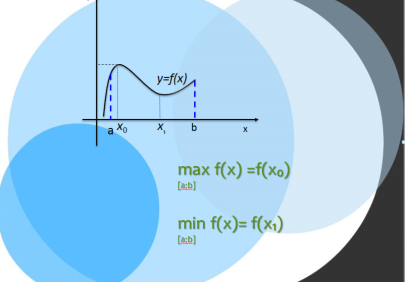
– Найбільше значення функції на [a,b] – це найбільше значення функції на цьому відрізку

– Найменше значення функції на [a,b] – це найменше значення з усіх на цьому відрізку.

Приклад  . f(x)=3х4- 6х2 +1,   [0;2]

Розв’язання:

1. D(f)=R
2. [0;2]  Є D(f)
3. f ́ (x)=12x3 -12x
4. f́(x)=0,  12x(x2 – 1)=0

                  12x(x-1)(x+1)=0

                  x=0;  x=1;  x=-1

5. 0   є [0;2], 1 є [0;2], -1 ¢ [0;2]

6. f(0)=1    f(1)=-2

 f(2)=3·16 - 6·4+1= 48 – 24 + 1=25

7. max f(x)= f(2)=25

    [0;2]

    min f(x)= f(1)=-2

     [0;2]

Алгоритм знаходження найбільшого і найменшого значення функції f(x) на відрізку.

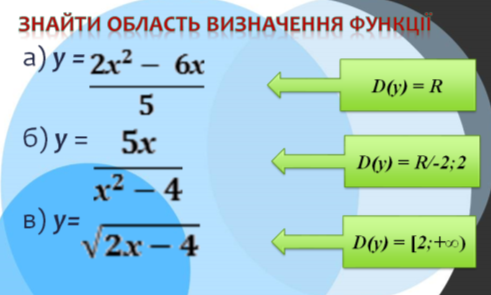
1.     Знайти область визначення функції D(f).
2.     Визначити чи належить заданий відрізок D(f).
3.     Знайти похідну функції f́̕(x).
4.     Знайти критичні точки функції, розв’язавши рівняння f́́̕(x)=0.
5.     Визначити, які з критичних точок належать даному проміжку.
6.     Знайти значення функції на кінцях проміжку та в критичних точках, що належать даному проміжку.
7.     Вибрати з одержаних значень найбільше і найменше. Записати відповідь.

1. Задача №1, 2 – опрацювати по підручнику.(с.129, п.24)
2. Розв’яжемо разом

Приклад 1. Знайдіть найбільше та найменше значення функції  на проміжку [0;3].

Розв’язання.

1) D(f) = R, розглядуваний проміжок належить області визначення.

3) Похідна існує в усіх точках; розв’язки рівняння х² + х - 2 = 0, тобто х₁ = 1; х₂ = -2 - критичні точки.

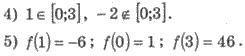
6) Отже, найбільше значення функції f(x) на заданому проміжку f(3) = 46, а найменше - f(1) = -6.

7) Це записують наступним чином:

№24.1, 24.3 виконати колективно

Підготовка до НМТ/ЗНО 

Завдання 1. Знайти різницю найбільшого та найменшого значення функції: f(x)=x² + (16-x)² на [8;16]

VІ. Підсумок уроку.

V. Завдання додому.
п. 24 опрацювати, виконати завдання № 24.2, 24.4