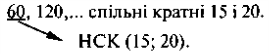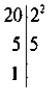Урок "Найменше спільне кратне"

 

 

 

 

 

УРОК

по темі

 

 

в 6 класі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2013 р.

Тема уроку: Найменше спільне кратне кількох натуральних чисел

Навчальна мета уроку:

• сформувати уявлення учнів про поняття спільного кратного кількох натуральних чисел;
• сформувати поняття учнів про найменше спільне кратне;                             
• навчити учнів користуватися алгоритмом знаходження НСК двох (трьох і т.д.) натуральних чисел;

Розвивальна мета уроку:

• розвивати навички логічного мислення;
• розвивати пізнавальну активність учнів;
• тренувати математичну пам’ять.

Виховна мета уроку:

• формувати навички самостійної діяльності учнів;
• виховувати увагу, організованість;
• розвивати творчу і пізнавальну активність.

Обладнання: презентації учнів по темі «Найменше спільне кратне кількох натуральних чисел»,  ребуси учнів, теоретичний матеріал, таблиці.

Тип уроку: засвоєння нових знань.

Очікувані  результати:

• систематизування знань учнів по темі «Подільність чисел»;
• вдосконалення в учнів умінь та навичок розв’язання задач.

Структура уроку:

1. Організаційний етап.         2 хв.
2. Актуалізація опорних знань учнів.               5 хв.
3. Формування нових знань               10 хв.
4. Закріплення знань і формування вмінь   12 хв.
5. Самостійна робота        8 хв.
6. Підсумок уроку.         3 хв.
7. Домашнє завдання.        2 хв.
8. Рефлексія.             3 хв.

 

Девіз уроку:                                                                                                                                                                                                                                                 

“ Я мислю –  отже, я існую. ”
Рене Декарт.

 

Хід уроку:

1.                  Організаційний етап.

Доброго дня! Я вітаю вас на уроці математики.

Сьогодні на уроці ми навчимося на основі раніше отриманих знань знаходити спільне кратне кількох натуральних чисел (НСК), а та­кож навчимося користувач

тися алгоритмом знаходження НСК двох (трьох і т.д.) натуральних чисел.

ІІ. Актуалізація опорних знань

1. Перевірка домашнього завдання

 Для більш цікавого протікання процесу перевірки домашнього зав­дання на уроці запропонувати учням провести цю роботу в ігровій формі, наприклад у вигляді гри «Знайди помилку». (Учи­тель заздалегідь записує на дошці розв'язання вправ домашньої ро­боти, припустившись кількох типових помилок. Учні, перевіряючи написане, повинні знайти помилку; можна організувати змагання: хто знайде більшу кількість помилок і зуміє їх пояснити.)

Для «слабких» учнів, домашнє завдання яких учитель перевіряє перед уроком, у цей час можна запропонувати роботу з картками-підказками.               Слайд 1.

 

Знайди НСД чисел 20 і 16. а) Розклади кожне з чисел на прості множники;
б) Підкресли в розкладах цих чисел однакові прості множники, в) Знайди серед підкреслених однакових ті, що мають менший показник степеня, г) Знайди добуток цих степенів

2. Запитання до класу:

• Відомо, що а, b, с — натуральні числа і а = bс.

Як можна назвати число а по відношенню до b?  по відношенню до а?

• Назвіть найменші три натуральних числа, кратних 2; 5; а.

3.Прийом «Мозкова атака»

1. Дайте відповідь на запитання:       Слайд 2.

• Число називається простим  якщо воно має:

 1). 1 дільник; 2). 2 дільника; 3). 3 дільника.

• Число ділиться націло на 9, якщо сума цифр ділиться націло на

1). 2;   2). 3;   3). 9.

2. Виконайте усні вправи:

• Позначте кількість простих дільників числа 24.

1). 2;   2). 3;   3). 4.

• Позначте число, яке ділиться і на 2, і на 3, але не ділиться на 5.

1). 15;  2). 16;  3). 102.

Надалі нас чекає маса задач, пов’язаних з трикутниками, їх елементами,

видами та властивостями.

IІІ. Формування нових знань

 Підходи до викладання теми НСК і НСД дуже схожі, тому цей етап уроку

проводиться аналогічно до відповідного етапу попе­реднього уроку.

1. Постановка проблеми

Задача. До кіоску завезли зошити. Якщо розкласти по 15 зошитів або по 20 зошитів в пачку, то в обох випадках зайвих зошитів не залишиться. Яку (найменшу) кількість зошитів могли завезти до кіоску? Яка наймен­ша кількість зошитів могла бути завезена?

Аналіз умови приводить до висновку, що під час розв'язування за­дачі треба знайти числа, які діляться (кратні) на 15 і на 20.

2. Розв'язання проблеми

Учні знайомляться з поняттями:

• кратне кількох натуральних чисел (Кратним натуральному числу а називають натуральне число, яке ділиться на а без остачі.);                              Слайд 4.   
• спільне кратне кількох натуральних чисел, найменше спільне кратне (НСК) (Найменше спільне кратне (НСК) кількох чисел – таке найменше натуральне число, яке ділиться на кожне з даних чисел);                              Слайд 5.   
• алгоритм знаходження НСК кількох чисел.     Слайд 6.   

Короткі нотатки можна оформити у вигляді такого конспекту:

 

НСК 1. Числа, кратні 15: 15; 30; 45; 60; 75; 90; 105; 120;... Числа, кратні 20: 20; 40; 60; 80; 100; 120;...
а)		б)15 = 3 · 5, 20 = 22 · 5;   в) НСК(15; 20) = 22 · 3 · 5 = 60.
Зауваження. Спільні кратні і — це числа виду , де п — нату­ральне число

 

Розв'язок задачі: НСК(15; 20) = 60, отже, найменша кількість зоши­тів 60; можливі варіанти 120, 180, 60п зошитів.

ІV. Закріплення знань і формування вмінь

Тренувальні вправи

І рівень

Усні вправи

1. Яке число називають спільним кратним а і b?
2. Яке число називають НСК чисел а і b?

II рівень

Письмові вправи

1. Випишіть усі прості числа, які більші за 10 і менші за 20.
2. Розкладіть на прості множники число 420.
3. Знайдіть таке значення х, що 25 < х < 35 і яке є спільним дільником чисел

52 і 78.

4. Яке найбільше двоцифрове число ділиться на 13?        Слайд 7, 8.
5. Знайдіть найменше спільне кратне чисел:  34; 51 і 68   Слайд 9.
6. В понеділок Чебурашка, Карлсон і Вінні-Пух  одночасно відправилися в довготривалу подорож  по казковій країні. Казкові герої надсилають про себе повідомлення: Чебурашка через кожні 6 днів,  Карлсон – 12 днів, Вінні-Пух - 9 днів.  Через скільки днів і в який день неділі одночасно прийдуть звістки  від всіх трьох казкових героїв?                                                         Слайд10, 11.   

 

V. Самостійна робота.        

Початковий і середній рівень

1. Напиши всі дільники числа 48.        (1; 2; 3; 4; 6; 8; 12; 16; 24; 48).

2. Напиши п’ять чисел, кратних числу 12.             (12; 24; 36; 48; 60…).

3. Які з чисел 5; 75; 315; 420; 495; 75432; 5346; 76050 діляться на 2; на 5; на 10?

( На 2: 420; 75432; 5346; 76050.      На 5: 15; 75; 315; 420; 495; 76050.

 На 10: 420; 76050).

Достатній рівень

1. Напиши всі дільники числа 10.        (1; 2; 4; 5; 10; 20; 25; 50; 100).

2. Напиши три найменші натуральні числа, кратні числам 5 і 7.      (35; 75; 105).

3. Розклади на прості множники числа: 186; 2240.    (186 = 2∙3∙31,2240 = 2⁶∙5∙7).

Високий рівень

1. Знайди НСД і НСК чисел 48 і 72.     (НСД = 24, НСК = 144).

2. Напиши розв’язки нерівності, кратні числу 10: 815 < х ≤ 870.

                                                            (820; 830; 840; 850; 860; 870).

3. Розклади на прості множники числа: 258; 5724.    (258=2∙3∙43, 5724= 2²∙3³∙53).

4. Знайди значення виразу 3а² - 5а², якщо а=0,2.                                 (-0,08).

Слайд 12 - 14.   

VI. Підсумок уроку

Наш урок наближається до завершення. Підбиваючи підсумки, слід наголосити, що основний зміст теми «Подільність чисел» розглянуто, тому основна мета наступного уроку — дооп­рацювати теми НСД і НСК і показати розуміння вивченого матеріалу і вміння його застосовувати для розв'язування відповідних вправ.  Всі вірно відповідали на запропоновані питання. Дякую за активну працю на уроці. 

VІI. Домашнє завдання.

1. Знайдіть найменше спільне кратне чисел: а) 50 і 75; б) 120 і 180; в) 370 і 740.
2. На скільки НСК (80, 100) менше за НСК (7, 100)?
3. Яке найменше трицифрове число кратне числам 5 і 13?
4. Скласти ребус, із словом «Дільник».

VІIІ. Рефлексія.   Закінчити  речення:

• Сьогодні на уроці я навчився ...
• Сьогодні на уроці я повторив...
• Сьогодні на уроці мені сподобалось...
• Сьогодні на уроці мене здивувало...
• Сьогодні на уроці я поставив собі оцінку...