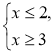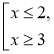Урок " Нерівності . Числові проміжки. Об’єднання та переріз числових проміжків
Алгебра, 9 клас
Тема1. Нерівності.
Тема Числові проміжки. Об’єднання та переріз числових проміжків.
Очікувані результати навчально – пізнавальної діяльності: учень/ учениця наводить приклади числових нерівностей зі змінними; лінійних нерівностей з однією змінною, подвійних нерівностей; формулює : властивості числових нерівностей, нерівностей зі змінною; обгрунтовує властивості числових нерівностей; розв’язує лінійні нерівності з однією змінною.; записує розв’язки нерівностей у вигляді об’єднання числових проміжків.
Обладнання: підручник Алгебра 9 клас (О.С. Істер ) , https://lib.imzo.gov.ua/wa-data/public/site/books2/pidruchnyky-9-klas/05-algebra-9-klas/ister-algeb-p-9ukr-054-13-s.pdf
ІНТЕЛЕКТУАЛЬНИЙ ФІТНЕС
-
Яке з чисел: 2; -0,2;
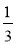 — є розв'язком:
— є розв'язком:
1) нерівності 2х – 1 < 0; 2) системи нерівностей 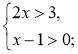
3) сукупності нерівностей 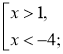 4) рівняння 5х – 1 = 9?
4) рівняння 5х – 1 = 9?
-
Де на координатній прямій містяться числа, якщо вони:
- більші за число 3;
- менші за число 3;
- більші за число 3, але менші від числа 5;
- є розв'язками рівняння | x | = 3?
Скільки таких чисел існує в кожному з випадків 1—4?
ТЕОРЕТИЧНИЙ БЛОК
1.Вивчи основні теоретичні відомості.
§5, підручник Алгебра, 9 клас (О.С. Істер )
2. Оформи опорний конспект , запиши в зошит, запам’ятай властивості
Опорний конспект
|
|
Числовий проміжок — вид запису множин, що є розв'язками нерівностей з однією змінною. Види числових проміжків |
|
|
|
|
Проміжок |
Приклад |
|
|
|
1. а < х < b
|
2 < x < 3
|
|
|
|
2. а ≤ х ≤ b
|
2 ≤ х ≤ 3
|
|
|
|
3. х > а
|
х > -2
|
|
|
|
4. х ≥ а
|
х ≥ -2
|
|
|
|
5. х < а
|
х < 3
|
|
|
|
6. х ≤ а
|
х ≤ 3
|
|
|
|
Переріз і об'єднання проміжків
Приклад 1. Розв'яжемо систему нерівностей
|
|
|
|
Розв'язання. (3; 5) — спільна частина проміжків (3; + ∞) і (-∞; 5), тому (3; 5) — це переріз проміжків (3; + ∞) і (-∞; 5) (розв'язок системи
Відповідь: (3; + ∞) |
|||
|
Приклад 2. Розв'яжемо систему нерівностей |
|||
|
|
|||
|
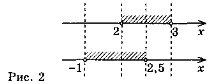
Розв'язання. Проміжок (-1; 3) складається з чисел, які є розв'язком хоча б однієї з нерівностей 2 < х < 3 або -1 < х < 2,5, тому є об'єднанням цих проміжків (розв'язком сукупності).
Відповідь: (2; 3) |
|||
Якщо точки — кінці проміжку включені в проміжок, їх позначають зафарбованими кружечками, якщо не включені — порожніми кружечками (їх називають «виколотими» точками). Якщо точки — кінці проміжку включені в проміжок, то для запису використовують квадратні дужки, якщо не включені — то круглі дужки.
ПРАКТИЧНИЙ БЛОК
Робота з підручником . Виконай завдання № 150,151, 155,157,159, 161, 163*
БЛОК КОНТРОЛЮ
- Чи належить проміжку [-7; -4] число:
1) -10; 2) -6,5; 3) -3; 4) 1?
- Чи належить проміжку (-4; 2) число:
1) 3,5; 2) -1; 3) 1,2?
- Укажіть найбільше ціле число з проміжку:
1) [-1; 4]; 2) (-∞; 3); 3) (-∞; -2,5).
Установіть відповідність між нерівностями та проміжками:
|
1) x > 3 2) х ≥ 3 3) 2 ≤ х < 3 4) х ≤ 3 5) х ≤ 2
6)
7) |
а) (-∞; 3) б) (3; +∞.) в) (-∞; 2]
г) (-∞; +∞) є) [2; 3) ж) (-∞; 3] |
Які записи зайві? Відповідь обґрунтуйте.
Домашнє завдання: §5, № 156, 158, 160,162.


про публікацію авторської розробки
Додати розробку

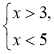 (рис. 1).
(рис. 1).
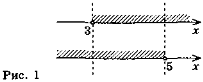
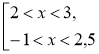 (рис. 2).
(рис. 2).