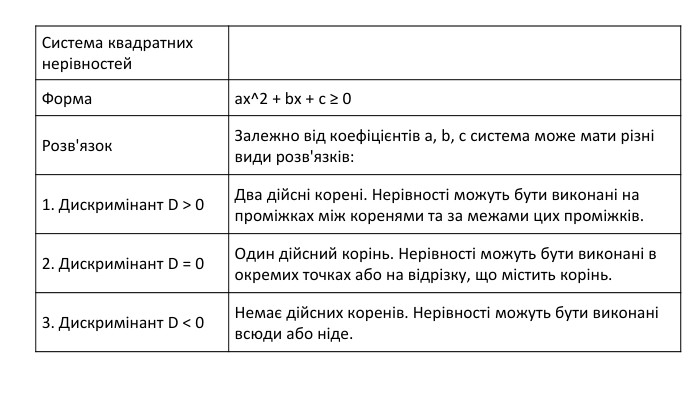
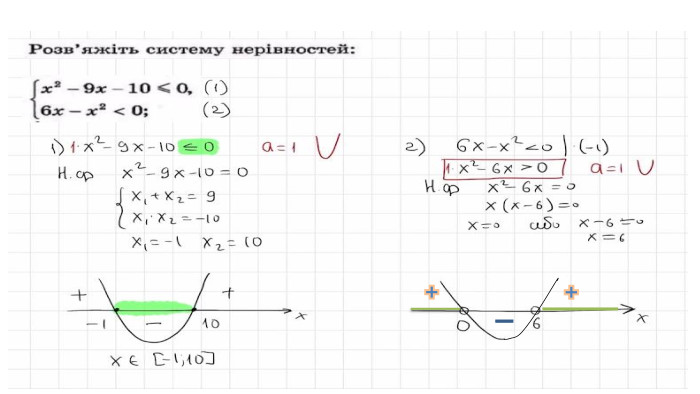
Системи квадратних нерівностей
Про матеріал
Матеріал буде корисним для всіх учасників навчального процесу. Презентацію складено за допомогою штучного інтелекту. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку