Урок "Об'єм призми та циліндра".

Тема програми: «Об’єми та площі поверхонь геометричних тіл».

Тема уроку: «Об’єм призми та циліндра».

Тип уроку: урок засвоєння нових знань.

Вид уроку: урок-бесіда.

Формування компетентностей:

предметна компетентність: узагальнити й систематизувати знання учнів про призму й циліндр, про властивості об’єму; домогтися засвоєння формул для обчислення об’ємів призми та циліндра; сформувати вміння розв’язувати задачі на обчислення об’ємів призми та циліндра;

ключові компетентності:

спілкування державною мовою – чітко та грамотно висловлюватися рідною мовою;  

математична компетентність – оперувати геометричними об’єктами в просторі, розв’язувати задачі, зокрема практичного змісту;  

уміння вчитися впродовж життя – усвідомлювати цінність нових знань і вмінь для обраної професії.  

Методи та прийоми: евристичний,  спонукально-пошуковий; робота з підручником та з моделями геометричних фігур.

Обладнання: 

1. Роздатковий матеріал (підручники Г. Бевз  «Математика 11 клас»).
2.     Дошка (записано число, тема, рисунки до вправ);
3.     Презентація уроку;
4.     Індивідуальні картки з кросвордами;
5.     Моделі циліндра, призм, паралелепіпеда;
6.     Моделі геометричних тіл.

Міжпредметні зв’язки:  алгебра, креслення, фізика.

Структура уроку:

1. Організаційний момент.
2. Перевірка домашнього завдання.
3. Актуалізація опорних знань учнів.
4. Формування  нових знань, умінь та навичок.
5. Закріплення нового матеріалу.
6. Підведення підсумків уроку.
7. Домашнє завдання.

Хід уроку.

1. Організаційний  момент (рапорт, привітання, перевірка наявності  ручок, олівців, лінійок, зошитів). (Слайди 1,2).

                                                  Девіз уроку:

•         Що є найбільшим  у світі?
• Простір.
• Що є найсильнішим?
• Розум.
• Що є найприємнішим?
• Досягти бажаного.

2. Перевірка домашнього завдання.

        Перевіряю наявність письмової домашньої роботи в зошитах.

3. Актуалізація опорних знань учнів

Сьогодні на уроці, ми продовжимо вивчати об'єми геометричних тіл і покажемо важливість    теми у професії електрогазозварник. А от яка тема сьогоднішнього уроку, ви довідаєтеся після розв'язання кросворда.

1. самостійна робота (по результатам написання самостійної роботи з’ясуємо тему нашого уроку) (Слайди 3,4):

І варіант

Питання до кросворда

1. Пряма призма, у основі якої лежить правильний многокутник (правильная).
2. У правильній призмі рівні прямокутники - бічні... (грани).
3. Два рівних многокутники призми, що лежать у паралельних площинах (основания).
4. Ребра призми, які не є сторонами основ, - це бічні... (рёбра).
5. Якщо всі грані паралелепіпеда є прямокутниками, то паралелепіпед називається... (прямоугольным).
6. … одиничного куба дорівнює одиниці об’єму (объём).
7. Переріз тіл обертання площиною, що проходить  через вісь називають … (осевым).
8. Призма, у якої бічні ребра перпендикулярні до площин основ (прямая).

(відповіді на питання до кросворда записати російською мовою).

ІІ варіант

Питання до кросворда

1. Віссю циліндра називається пряма, що проходить через … основ (центры).
2. Відрізки, що сполучають відповідні точки основ циліндра (образующие).
3. Призма, основою якої є паралелограм (параллелепипед).
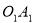4. - це …  циліндра (рис. 1) (радиус).                                                  

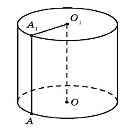            рис. 1

5. …  циліндра рівні і лежать у паралельних площинах (основания).
6. Чи бажаєш ти бути атестованим з математики?
7. Якщо твірні циліндра перпендикулярні площинам основи, то такий циліндр  називається … (прямым).
8. Відстань між основами циліндра (высота).

(відповіді на питання до кросворда записати російською мовою).

(питання до кросворда на дошці; обговорюємо результати написання самостійної роботи, при цьому на кожен пункт кросворда пропоную додаткові питання:

І варіант.

1. Серед пропонованих геометричних фігур вказати на пряму та правильну призми;
2. На обраній моделі вказати бічні грані, бічні ребра та основи призм;
3. Серед пропонованих геометричних фігур вказати на прямокутний паралелепіпед;
4. Які ще властивості об’єму вам відомі?

ІІ варіант.

5. На моделі циліндра указати вісь, твірну, радіус, основи та висоту циліндра.

Пропоную учням кросворд з відповідями та прочитати ключові слова).

2. записуємо в зошитах число та тему уроку (Слайд 5).;

3. мотивація навчальної діяльності:

Чи потрібно електрогазозварнику вивчати дану тему, знадобляться отримані на сьогоднішньому уроці знання в майбутньому? Для того, щоб відповісти на ці питання я пропоную вам розглянути дві задачі прикладного характеру (на дошці відкриваємо умови задач – слайд 6):

1.  Резервуар для води слід встановити на майданчику трикутної форми, що слугуватиме для нього дном. Якою має бути висота резервуара? Ємність резервуара 10 м³, площа майданчика  5 м².
2. Знайти ємність циліндричної цистерни діаметром 4 м і заввишки 5 м?

Для розв’язування задач суто практичного характеру вам необхідні формули, що будуть розглянуті сьогодні на уроці. Із цими формулами ви, до речі, уже частково знайомі.

4. Формування  нових знань, умінь та навичок:

          План вивчення теми:

1. Формула для обчислення об’єму прямої призми.
2. Формула для обчислення об’єму циліндра.
3. Приклади застосування формул для обчислення об’ємів призми та циліндра.   

Чому дорівнює об’єм прямокутного паралелепіпеда? (добутку площі основи на висоту).

А як знайти об’єм призми? На це питання зараз будемо знаходити відповідь.

Візьмемо дві рівні прямі призми, в основі яких лежить прямокутний трикутник, складемо прямокутний паралелепіпед. Як це можна зробити? (Слайд 7).

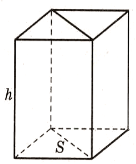
Якщо висота, площа основи та об’єм трикутної призми відповідно дорівнюють і , то висота, площа основи та об’єм прямокутного паралелепіпеда дорівнюють і . Так, як об’єм прямокутного паралелепіпеда дорівнює добутку площі основи на висоту, то

 = маємо: =

Отже, об’єм кожної прямої призми, в основі якої лежить прямокутний трикутник, дорівнює добутку площі її основи на висоту.

Якщо розглянути довільну призму з площею основи  , висотою об’ємом , то її основу можна поділити на прямокутних трикутників, а відповідно дану призму – на прямих призм, основами яких є прямокутні трикутники.

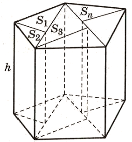
За таким же  алгоритмом знаходимо об’єм призми. Доводимо, що об’єм кожної прямої призми дорівнює добутку площі її основи на висоту.

Тепер розглянемо циліндр. (Слайд 8).Циліндр можна розглянути як правильну  -кутну призму при дуже великому значенні , наприклад мільярд. Така призма практично не відрізняється від циліндра. Тому об’єм циліндра також дорівнює добутку площі основи на висоту.

Яка фігура лежить в основі циліндра? (круг)

За якою формулою знаходять площу круга? ()

Отже, об’єм циліндра, радіус основи якого - , а висота - можна знаходити за формулою .

5. Закріплення нового матеріалу.

• Колективне розв’язування задач під керівництвом викладача (Слайд 9).:

(Пропоную повернутися до задач 1 і 2, які розглядалися на початку уроку, і розв’язати їх).

Розв’язання задачі 1 (розв’язують учні за допомогою допоміжних питань).

1. Яку геометричну фігуру вам нагадує резервуар (пряму трикутну призму)?
2. Чи відомий об’єм цієї фігури (10 м³)?
3. Чому дорівнює площа основи фігури (5 м²)?

Записуємо: Будемо розглядати резервуар як пряму призму об’ємом 10 м³, основою якого є трикутник площею  5 м².

4. За допомогою якої формули знаходимо об’єм призму (V =Sосн ⋅H)?

      Записуємо: Тоді V =Sосн ⋅H, де H – шукана висота,  Sосн =5 (м²), V=10 м³.

5. Як за допомогою цієї формули знайти висоту ()?

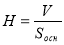Записуємо:

6. Знайдіть значення висоти та запишіть відповідь.

      Записуємо:   = 2 (м).

                          Відповідь: 2 м.

Розв’язання задачі 2 (учні розв’язують самостійно за допомогою алгоритму, записаного на дошці; для учнів з достатнім рівнем навчальних досягнень пропоную картки з індивідуальними завданнями). (Слайд 10).

1. Об’єм якої геометричної фігури вам необхідно знайти?
2. Запишіть коротку умову задачі.
3. Запишіть формулу.
4. Які елементи циліндра вам необхідно знати?
5. Які елементи вам не відомі і як їх можна знайти?
6. Знайдіть радіус.
7. Знайдіть об’єм.
8. Замість π підставите значення 3,14  і знайдіть ємність цистерни.

Перевірте: Дано:= 4 м; H =5 м.  V-?

                   Розв’язок: V = πR² ⋅H ,  R= = 4:2=2 м; тоді  V = π ⋅2² ⋅5=20π м³ =20⋅3,14≈63 м³.

                   Відповідь: ≈63 м³.

• Розв’яжіть задачу, заповнив пропуски.

Основою прямої призми являється трикутник зі стороною 5см і висотою 6 см, проведеною

до цієї сторони. Знайдіть висоту призми, якщо її об'єм дорівнює  120 см³.

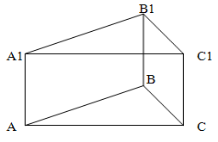
Дано:- призма; =… см; ;  …  =6 см.  V=120 см³

Знайти: … -?

Розв’язок: V =… ⋅H,   ;  Sосн = … ;  Sосн = … ⋅ 5 = … см²; 

                   тоді  = 8 … .

 Відповідь: … .

6. Підведення підсумків уроку 

  Інтерактивна вправа «Закінчіть речення»

1. Об’єм куба з ребром 2 см дорівнює...
2. Об’єм прямокутного паралелепіпеда з вимірами 3 см, 1 см, 2 см дорівнює...
3. Об’єм прямої призми знаходять за формулою V =...
4. Об’єм циліндра дорівнює...
5. Об’єм куба з ребром 3 см дорівнює...
6. Об’єм любої призми знаходять за формулою V =...
7. Рівні тіла мають…
8. Якщо многогранник складений із кількох многогранників, то його об’єм дорівнює…
9. Об’єм куба з ребром, що дорівнює одиниці довжини, дорівнює…

7. Домашнє завдання(Слайди 11,12) :   

1)    Г. Бевз, В. Бевз «Математика 11 клас».

                                     § 24   сторінка 214.

                                        2)    Розв’язати вправи № 903, № 933.

                                             Додаткове завдання: Скласти задачу, за темою об'єм призми та циліндра пов'язану із професією.