Урок Об’єми тіл обертання. Розв’язування задач професійного змісту

Державний навчальний заклад

«Нововолинський центр професійно-технічної освіти»

 

 

 

 

Об’єми тіл обертання.

Розв’язування задач професійного змісту

(Методична розробка уроку)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Панас Г.І.

викладач математики

 

 

 

 ВСТУП

Сучасне суспільство знаходиться у стані політичних та економічних змін. Тому для людини важливими є здатність бути мобільною та адаптивною, вміння бачити проблему, чітко формулювати та всебічно підходити до її розв’язування, здобувати необхідну інформацію тощо.   Чільне місце   належить математиці, адже вона була і залишається технічною мовою для вивчення різних предметів. Учні  повинні опанувати системою математичних знань, навичок та умінь, необхідних у повсякденному житті та майбутній трудовій діяльності .

Потяг до знань, високу пізнавальну активність та уміння самовдосконалюватися необхідно розвивати й виховувати у молоді під час навчання у професійних навчальних закладах. Проблема застосування знань на практиці вимагає формування в учнів уміння аналізувати й синтезувати ситуації, конкретизувати загальні абстрактні положення, пізнавати відомі фігури, залежності у конкретних ситуаціях, переусвідомлювати один і той самий об’єкт або явище під кутом зору різних систем знань, варіювати способи дій, переключатися з одного виду діяльності на інший.

 Розв’язування прикладних задач у  курсі математики сприяє ознайомленню учнів із роботою підприємств і галузей народного господарства, викликає інтерес до майбутньої професії, сприяє реалізації міжпредметних зв’язків, активізує різні процеси мислення. Вони  сприяють виконанню багатьох завдань навчального процесу.

            Важливим фактором  формування наукового світорозуміння є те, що математичні формули, теореми, різні залежності створюються під впливом практики і практичних потреб людини. Основними засобами реалізації професійної направленості на уроках математики є використання дидактичного матеріалу (питання, задачі, завдання професійного змісту). Зміст дидактичних матеріалів, орієнтованих на зв’язок із професією, певним чином направляє пізнавальну діяльність учнів. Робота з такими матеріалами може сприяти формуванню в учнів вміння знаходити в професійній ситуації суттєві ознаки математичного поняття, використовувати це поняття в нових умовах.

Дидактичні матеріали можуть бути направлені на розвиток просторової уяви, обчислювальних навичок і графічних умінь, на розширення їх професійного кругозору, на формування загальнотрудових умінь і навичок роботи з вимірювальними приладами, таблицями , довідниками.

 Добре дібрані задачі прикладного характеру сприяють пробудженню інтересу учнів до курсу математики, створюють впевненість в її корисності і практичній значимості. Тим самим ці заняття закріплять уявлення учнів про виникнення і розвиток геометрії в результаті практичної та виробничої діяльності людей .

 Робота зі складеною системою прикладних стереометричних задач виступає ефективним засобом активізації пізнавальної діяльності учнів. Це відбувається завдяки підвищенню пізнавального інтересу, досягається зосередженням уваги на значенні стереометричних знань у реальному житті.

Тема «Об’єми тіл обертання. Розв’язування задач професійного змісту » є однією із завершальних теми   «Геометричні тіла. Об’єми та площі поверхонь геометричних тіл». Тому цей урок вимагає чіткої організації, високої активності учнів, насиченості. На час проведення даного заняття учні уже засвоїли теоретичний матеріал і мають навички розв’язування основних типів задач.

Такий урок передбачає тісний зв'язок із вивченими раніше темами геометрії і спецтехнології (слюсар з ремонту автомобілів).

Дослідженнями циліндричних поверхонь і їх властивостей займалися досить давно.  Те, що всі точки кола однаково віддалені від центра, безпосередньо застосовується на практиці. Наприклад, в автомашині, завдяки коловій формі ободу колеса, вісь, на якій воно обертається при русі автомашини, весь час залишається на одному рівні від поверхні, по якій переміщується автомашина. Внаслідок цього забезпечується горизонтальне переміщення пасажирів або вантажу.

Зрозуміло , що не можна розв’язати задачу не володіючи теоретичним матеріалом. На уроці узагальнюються знання учнів, повторюються основні означення і властивості тіл обертання, закріплюються основні поняття і формули з теми, розвиваються практичні навички  учнів, вміння застосовувати набуті знання.

З метою активізації пізнавальної діяльності учнів, підвищення їх інтересу до предмету, розвитку самостійності , виховання організованості , відповідальності використано різні форми роботи на уроці.

Оскільки основною метою таких уроків є навчити учнів розв’язувати задачі, то організація такого процесу має велике значення (коментування у процесі розв’язування, аналіз задачі, контроль за правильністю розв’язку і виконання рисунків, вміння знаходити у певних деталях математичну модель… )

Здійснення індивідуального та диференційованого підходу не лише сприяє чіткій організації уроку, раціональному використанню навчального часу, а й посилює впевненість учнів у своїх силах.

   Отже,  вивчення стереометричного матеріалу в ПТНЗ  має носити практичний характер, базуватися переважно на дослідах, інтуїції, експерименті; тим самим буде сформовано необхідний запас просторових уявлень  на науково-теоретичному рівні для подальшого використання у майбутній професії.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема уроку.  

Об’єми тіл обертання. Розв’язування задач професійного змісту

 

Тип уроку. Урок систематизації та узагальнення вивченого матеріалу

 

Мета уроку.   Узагальнити та систематизувати знання учнів з теми; повторити поняття   циліндра, конуса, кулі, елементів цих фігур; формули для обчислення бічної, повної поверхонь, об’єму. Показати практичне застосування вивчених формул, за якими знаходяться об’єми та площі поверхонь тіл обертання, звертати увагу учнів на зв'язок предмета з життям. Застосувати математичні знання під час розв’язання прикладних задач. Розширювати кругозір учнів та їхню просторову уяву, формувати   логічне мислення, математичне мовлення; розвивати бажання пізнавати нове,  уміння працювати з додатковою літературою, довідковим матеріалом, комп’ютером. Прививати інтерес до математики. Виховувати почуття відповідальності, старанність у навчанні, вміння швидко і правильно приймати відповідні рішення; вчити орієнтуватися в нестандартних ситуаціях.

 

Обладнання: мультимедійний комплекс, карточки - завдання для самостійної роботи, залікові картки , моделі   тіл обертання, деталі автомобілів круглих форм, презентації, мікрокалькулятор.

 

Інтерактивні методи: робота в групах, вправа «уявний мікрофон», мозковий штурм,   реферати , «Метеоритний дощ» , «Вірю – не вірю».

 

Міжпредметні зв’язки: спецтехнологія, інформатика, алгебра     

       

Хід уроку

І. Організаційна частина.  Повідомлення теми та мети уроку.

          Викладач вітається, пропонує учням зайняти свої робочі місця.

Викладач. Сьогодні на уроці ми узагальнимо і систематизуємо ваші знання з теми «Об’єми тіл обертань».

ІІ. Мотивація навчальної діяльності.

          Викладач. Наше суспільство потребує як талановитих дослідників, так і спеціалістів, які добре знають математику та здатні застосувати свої знання на практиці. Застосування   математики в усіх галузях науки, господарства і життя необмежене. Математика скрізь, вона – на кожному кроці.

          ІІІ. Узагальнення та систематизація знань

          Викладач. Ми з вами завершуємо курс вивчення стереометрії. На уроках ми велику увагу приділяли стереометричним тілам. З’ясовували їх елементи та властивості, вчилися розв’язувати задачі на знаходження площ та об’ємів геометричних тіл. Про які тіла обертання ми вели мову?

             Мозковий штурм.

           Тіло… (циліндр, конус, зрізаний конус, куля, сфера…)

           Викладач. Проектується на екран  РОМАШКА, у якої порожні пелюстки. Ви повинні заповнити їх термінами, які мають відношення до тіл обертання.

           Вправа «Уявний мікрофон» Учні відповідають, тримаючи уявний мікрофон. Один учень записує на дошці відповіді, які потім звіряють із правильними на Слайді.

        

            Викладач: Думаю, кожен з вас розуміє важливість вивчення стереометрії, адже вона має тісний зв'язок з практичною діяльністю людини, з нашим побутом, з іншими науками. В цьому, гадаю, ви переконалися готуючись до сьогоднішнього уроку і переконуватимете своїх одногрупників.  Будете мати нагоду розповісти про свої відкриття та поділитися новими знаннями. Але перш ніж говорити про стереометричні тіла в житті, давайте пригадаємо теоретичний матеріал. 

  Фронтальне  опитування  (з використанням мультимедійного комплексу)

1.Дайте означення циліндра.

2.Назвіть елементи циліндра.

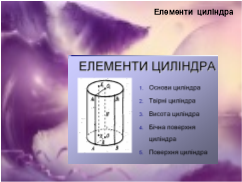
         3.Чому дорівнює площа бічної, площа повної поверхні та об’єм циліндра?

         4. Дайте означення конуса.

         5.Назвіть елементи конуса.

         6. Які властивості має конус?

         7.Чому дорівнює площа бічної, площа повної поверхні та об’єм конуса?

 

8.Дайте означення кулі.

                    9.Дайте означення сфери.

                   10.Чому дорівнює площа сфери та об’єм кулі?

                  

                   11. Формула для об’ємів тіл обертання

              

ІV. Актуалізація опорних знань.

1.На дошку проектуються формули для обчислення об’ємів та площ поверхонь тіл обертання. Учитель запитує, що можна знайти за допомогою даних формул (вправа «Мікрофон»).

                                        

 

                                                           

 

           

2. Вправа «Уявний мікрофон»

Учні відповідають, тримаючи уявний мікрофон. 

Питання:

 1. Що таке циліндр?

Циліндр - це геометричне тіло, що складається із двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів.

2. За якою формулою можна обчислити об’єм циліндра?

Об'єм циліндра дорівнює добутку площі його основи на висоту:

, де R – радіус, а H – висота циліндра

3. Що таке конус?

Конус – це геометричне тіло, що складається з круга, точки, яка не лежить у площині цього круга і всіх відрізків, що сполучають цю точку з точками круга.

4. Що таке твірні конуса?

Твірні - відрізки, що з'єднують вершину з точками основи.

5. Що таке висота конуса?

Висота - перпендикуляр, проведений з вершини до центра основи

6. Чому дорівнює площа бічної поверхні конуса?

Площа бічної поверхні конуса дорівнює половині добутку довжини кола основи на твірну:

де l - твірна.

7. Чому дорівнює об’єм конуса?

Об'єм конуса дорівнює одній третій добутку площі його основи на висоту:

8. Дайте означення кулі та її елементів

Кулею називається тіло, що складається з усіх точок простору, відстань від яких до даної точки не перевищує заданої. Ця точка - центр кулі. Радіус - задана відстань. Поверхня кулі називається сферою.

9. Чому дорівнює об’єм кулі?

Об'єм кулі дорівнює добутку площі її поверхні на третину радіуса:

Одночасно  три учні працюють над картками - завданнями. Кожен учень виконує своє  завдання і віддає їх вчителю. Оцінки за дане завдання будуть оголошені на наступному кроці.

 Картка 1. Циліндр

         1. Що таке радіус циліндра ?

         2. Що отримується в перерізі циліндра площиною

         - паралельною осі циліндра

         - перпендикулярною вісі циліндра?

         3. Якою геометричною фігурою є осьовий переріз прямого циліндра?

         4. Якою геометричною фігурою є бічна поверхня циліндра?

         5. Чому дорівнюють сторони осьового перерізу циліндра ?

Картка 2. Конус

         1.Якою геометричною фігурою є осьовий переріз конуса?

         2. Чому дорівнюють сторони осьового перерізу прямого конуса?

         3. В якій точці лежить основа висоти прямого конуса ?

         4. Якою геометричною фігурою є переріз конуса площиною, паралельною основі ?

         5. Як називається відрізок , що сполучає вершину конуса з точкою основи ?

Картка 3 . Куля

         1. Як називається відрізок, що сполучає центр кулі з точкою кульової поверхні?

         2. Як називається границя кулі ?

         3. Як називається переріз сфери діаметральною площиною ?

         4. Які точки кулі є діаметрально протилежними ?

         5. Яка геометрична фігура отримується в результаті перерізу кулі площиною?

         6. Як називається переріз кулі діаметральною площиною?

3. Реферативне повідомлення учнів

 (домашнє завдання , яке супроводжується мультимедійною презентацією)

           Викладач. З якими геометричними тілами ви зустрілись при вивченні спецтехнології ?

Виступ учня.  Тіла обертання в обладнанні автомобіля

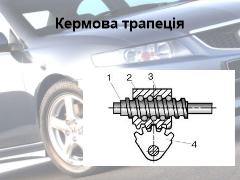
Тіла обертання широко застосовуються в техніці, особливо в автомобілебудуванні. В цьому можна переконатися, якщо подивитися на форму різних приладів, агрегатів. Найпростіша деталь автомобіля —підшипник —.має в своєму складі тіло обертання—- кулю. Але чому саме кулю, а не куб або призму? Та тому, що куля зазнає найменшого тертя під час роботи підшипників. У них вставляються кульки однакового розміру. Не можна вставити хоча б одну кульку більшу або меншу за розміром, бо це спричиняє люфт агрегатів автомобіля і призводить до ушкоджень. Важливим є також те, що складові частини кермової трапеції з'єднані не простими болтами, а кульовими з'єднаннями Бо під час повороту змінюються кути з'єднання і циліндричні болти можуть зламатися. Ще кулі використовують:

а) при перемиканні передач — кульки не дають змоги увімкнути відразу дві передачі;

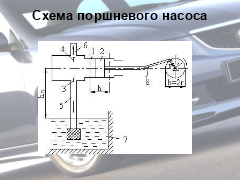
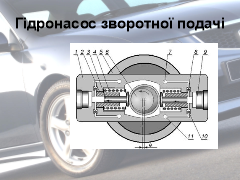
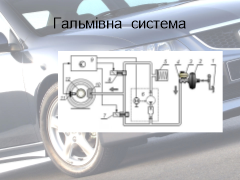
б) у клапанних пристроях — у гідровакуумних насосах кулька перекочується в циліндрі під тиском або в результаті розряду то відкриває, то закриває шлях гальмовій рідині;

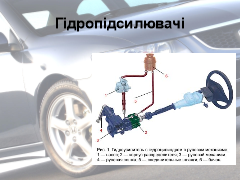
в) у гідропідсилювачі — при повороті керма перекочується в бік повороту і допомагає водієві повертати кермо.

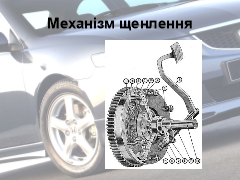
Важливу роль в автомобілі відіграють циліндри. Циліндричні підшипники в автомобілях використовують там, де потрібні підшипники з великою бічною поверхнею і невеликою товщиною (наприклад, у механізмі зчеплення).

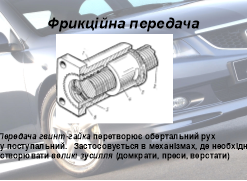
У формі циліндра зроблено найважливіші складові частини автомобіля: генератор, індукційну котушку, конденсатори, фільтри, насоси, стартер, карданну передачу, гідропідсилювач тощо. Тут використовується така властивість обертання навколо своєї осі: відстань від усіх зовнішніх точок до осі обертання однакова, що якраз ми спостерігаємо у циліндрі.

Головні робочі частини двигуна — поршні — теж мають форму циліндрів і знаходяться в своєрідних циліндрах. Під час переміщення поршня від верхньої мертвої точки до нижньої мертвої точки над ним утворюється простір, який називається робочим об'ємом циліндра. Коли поршень знаходиться у верхній мертвій точці, над ним утворюється найменший простір, який називається об'ємом камери згоряння.

У багатоциліндрових двигунах повний об'єм усіх циліндрів виражається в літрах і називається літражем. Таким чином, визначення об'ємів циліндрів є головною характеристикою автомобіля.

Чи використовуються в автомобілі конуси? У формі конусів виконано багато регулюючих гвинтів у різних частин; автомобіля (наприклад, на колесах). Використовуються також конічні підшипники. Голчасті клапани, виготовлені у формі конуса, використовуються у карбюраторі для регулювання подачі конуса виготовлені деякі  деталі двигуна (головки клапанів, кульові пальці, поршень у головному гальмовому циліндрі).

Усе це свідчить про те, що такі тіла обертання, як куля, циліндр, конус, широко застосовуються як в автомобілебудуванні, так і в деяких інших галузях діяльності людини.

Презентація 3

 

 V. Розв’язування задач.

1. Робота в малих групах ( 15 хв. ).

Викладач. Зараз пересаджуємось у  відповідні    групи по три учні. На столах лежать залікові картки з трьома видами завдань: «Метеоритний дощ» (допиши те, що змило дощем); «Вірю – не вірю» (вибрати вірне ствердження); задача. Кожна група виконує своє  завдання і віддає їх вчителю. Оцінки за дане завдання будуть оголошені на наступному кроці.

Залікова картка І групи 

1.	«Метеоритний дощ»	V = 1/3 … R..H V = 1/3πH(R12 + … + R22)  1 бал
2.	«Вірю – не вірю»	У конуса радіус основи ОА = 8 см, а висота  СО =15 см. Які з наведених затверджень вірні, а які ні: а) катети прямокутного трикутника СОА дорівнюють 17 і 8 см; б) осьовий  переріз конусу – прямокутний трикутник з гіпотенузою СА = 17 см; в) твірна конуса дорівнює 15 см; г) об’єм конуса дорівнює 1/3π8215 см3.    2 бали
3.	Задача	Висота конусу 6 см, твірна 10 см. Знайти об’єм конуса.  2 бали

Залікова картка ІІ групи 

1.	«Метеоритний дощ»	V =  … R..H S… = 2πR ( … + R)  1 бал
2.	«Вірю – не вірю»	Об’єм циліндра дорівнює 250π см3 . Які з наведених затверджень вірні, а які ні: а) об’єм циліндра дорівнює добутку площі основи на висоту; б) площа основи циліндра дорівнює 25 см2; в) радіус циліндра  дорівнює 10 см; г) радіус циліндра вдвічі менше за його твірну.    2 бали
3.	Задача	Осьовий  переріз циліндра – квадрат, діагональ якого дорівнює 4√2 см. Знайти об’єм циліндра.  2 бали

Залікова картка ІІІ  групи 

1.	«Метеоритний дощ»	V = …/3 … R.. V = 2/3π……H  1 бал
2.	«Вірю – не вірю»	Об’єм кулі дорівнює 36π см3, висота кульового сегмента дорівнює 1/3 діаметру кулі. Які з наведених затверджень вірні, а які ні: а) радіус кулі  дорівнює 3 см; б) об’єм кульового сегмента відноситься до об’єму кулі як 7:27; в) діаметр кулі дорівнює 8 см; г) площа кулі дорівнює 36π см2    2 бали
3.	Задача	Радіус трьох куль дорівнюють 3, 4, 5 см. Знайти радіус кулі, об’єм якої дорівнює сумі об’ємів  даних куль.  2 бали

  2. Одночасно учні біля дошки розв’язують задачі

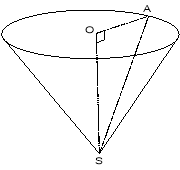        Задача  1.Фільтр має форму перевернутого конуса. Скільки рідини міститься у фільтрі, якщо радіус його основи дорівнює 10см, а довжина від дна до краю (твірна) – 26см?

 

 

 

 

 

        Задача 2. Чавунна куля регулятора має масу 10 кг. Знайти діаметр кулі, якщо густина чавуну 7,2 г/см³.

        3.Розв’язування практичних задач. (розв’язати задачі відповідно до часу)

Задача 1. Знайти об’єм пальної суміші в циліндрі автомобіля КамАЗ, знаючи, що внутрішній діаметр циліндра 120 мм, а робочий хід поршня 120 мм.

Відповідь. .

Задача 2. Ролик радіально-опорного підшипника має форму зрізаного конуса з діаметрами основ 5 мм і 6 мм та висотою 7 мм. Знайти об’єм матеріалу, з якого виготовлено ролик.

Відповідь. ≈.

Задача 3. Редукційний клапан двигуна автомобіля ГАЗ 53 має форму кулі діаметром 8 мм. Знайти об’єм клапана.

Відповідь. .

Задача 4 .Ролик підшипника кочення має форму циліндра, висота якого 20 мм, діаметр основи 10 мм. Знайти об’єм матеріалу, з якого виготовлено ролик.

Відповідь. .

Задача 5. Скільки тонн бензину можна зберігати в цистерні циліндричної форми, якщо її діаметр 4 м, а довжина 3 м? (Густина бензину 700 кг/м³.)

        Відповідь. 26,376 (т).

Задача 6. Маса кульки дворядного сферичного підшипника дорівнює 3 г. Який її діаметр (p = 7,8 г/см³)?

Відповідь. .

 

     Викладач: Я думаю, що кожен з вас переконався у важливості вивчення стереометричних тіл, адже вони тісно пов’язані з нашим життями, але в практичній діяльності ми на лише дивимось на тіла, а й працюємо з ними. Тому пропоную вам попрацювати над практичними задачами.

Підсумок уроку

Оцінити знання учнів на уроці

Викладач:

Минають роки… Геометрія збагачується новими фактами, змінює свій погляд. Були часи, коли вона, як при Платоні чи Піфагорі, займала становище справжньої цариці наук, а були часи, коли вона в своєму розвитку починала відставати від інших, молодих наук. Але ніколи, очевидно, поки стоїть світ, не настане такий час, коли б людство могло сказати: «ось тепер геометрія не потрібна і залишається здати її в архів». Геометрія була, є і буде постійною супутницею людини на всьому шляху її розвитку.

Сьогодні ми повторили означення, основні властивості  тіл обертання та формули для обчислення площ поверхонь та об’ємів тіл, застосували ці знань при розв’язанні задач з прикладним змістом. І як підсумок до уроку хочу нагадати вам слова Рене Декарта «Теорія без практики мертва і безплідна, практика без теорії неможлива».

Домашнє завдання

1.

 

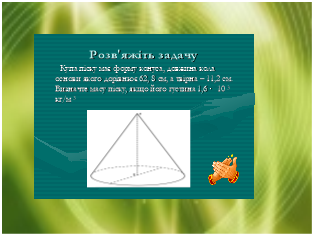
2. Скласти дві задачі прикладного змісту на обчислення площ поверхонь та об’ємів тіл обертання  та розв’язати їх.

 

 

 

 

 

 

Список використаних джерел

1. Бевз Г.П. Геометрія в загальноосвітній школі/ Г.П.Бевз//Математика в школах України.-2003.-№1.- с.18.

2. Возняк Г., Маланюк М. Взаємозв'язок теорії з практикою в процесі вивчення математики. — К.: Рад. шк., 1989.

3. Волосюк О.В., Онопченко С.В. Педагогічні аспекти прикладної спрямованості шкільного курсу математики.//Вісник ЛНУ імені Тараса Шевченка. – 2010. – № 17 (204). – С.36-40.

4. Возна М. Спроби формування цілісної картини навколишнього світу в процесі навчання математики// Математика в школах України.-2005.-№30.

5. Державний стандарт базової і повної середньої освіти //Математика в школі.-2004.-№2.

6. Погорєлов О.В. Геометрія. Підручник для 10-11 класів. – Київ: «Освіта», 2001.

7. Тадеєв В.О.  Геометрія. 11 клас. Дворівневий підручник. – Тернопіль: Навчальна книга – Богдан, 2004.

8. ЧерватюкО.Г. , Шиманська Г.Д. Елементи цікавої математики на уроках математики. – Київ: «Радянська школа», 1968.