Презентація "Трикутник". Підготовка до ЗНО
Презентація до уроку узагальнення в 11 класі з теми "Трикутник". Матеріал використаний з завдань ЗНО основної та додаткових сесій. Можна використовувати і в 9 класі для підготовки до ДПА








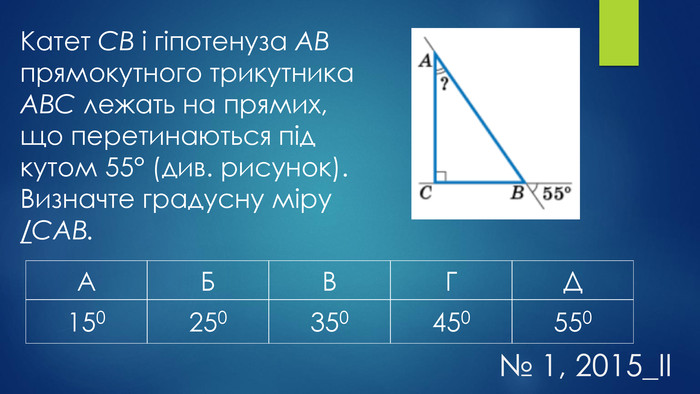

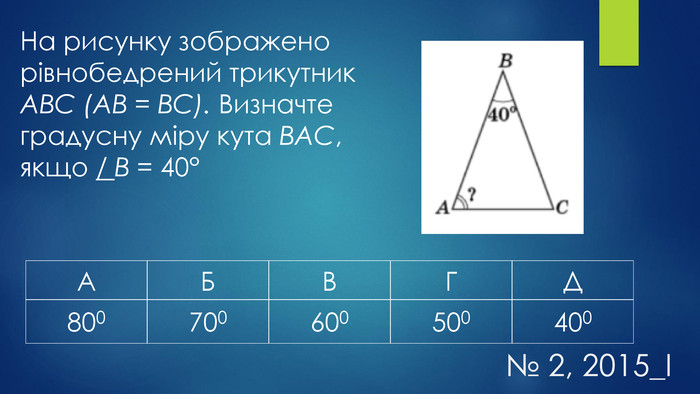




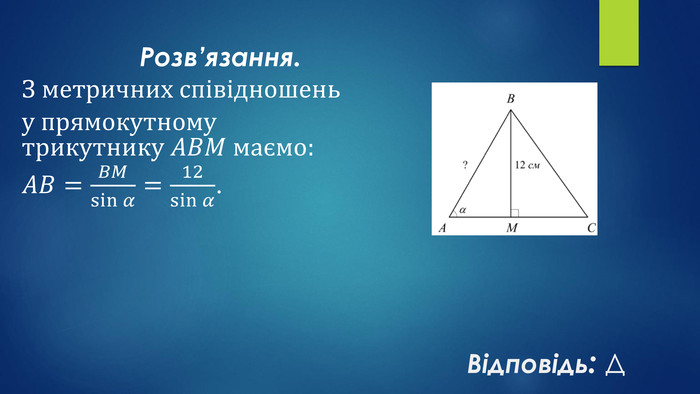

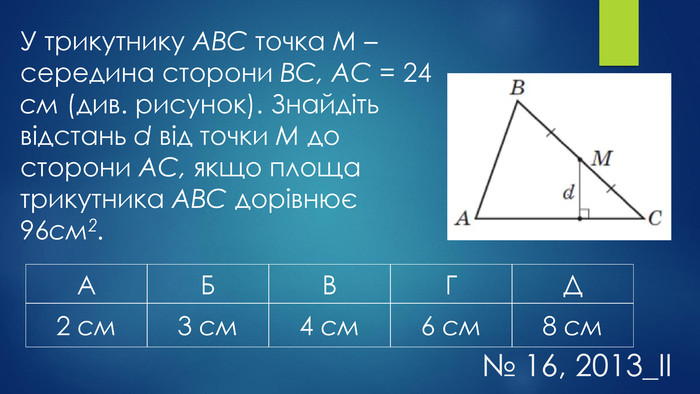

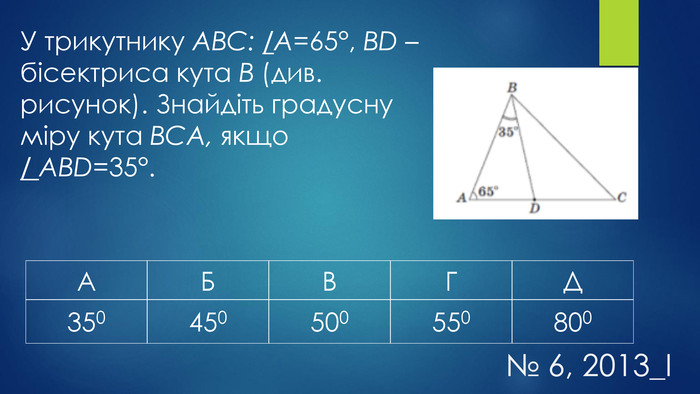

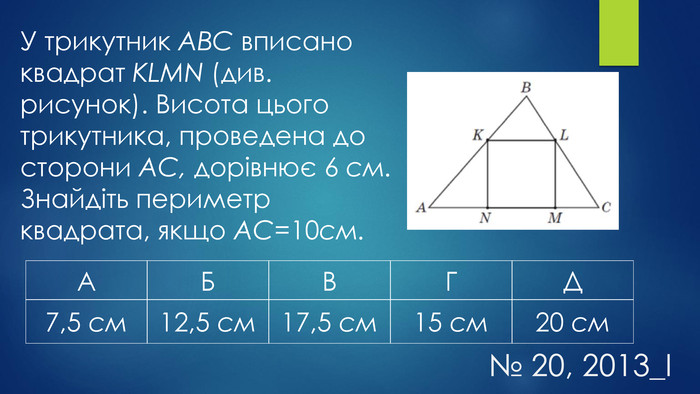


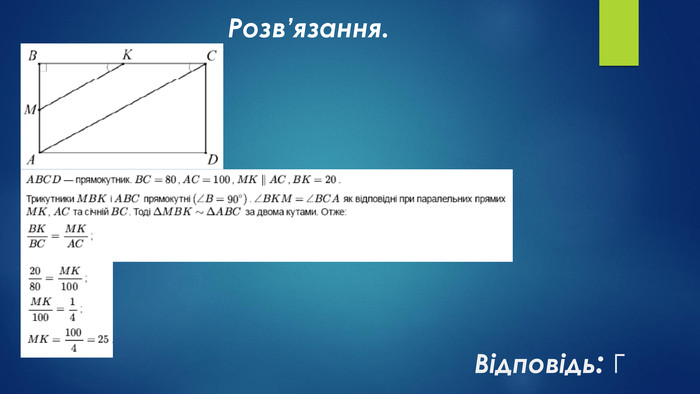






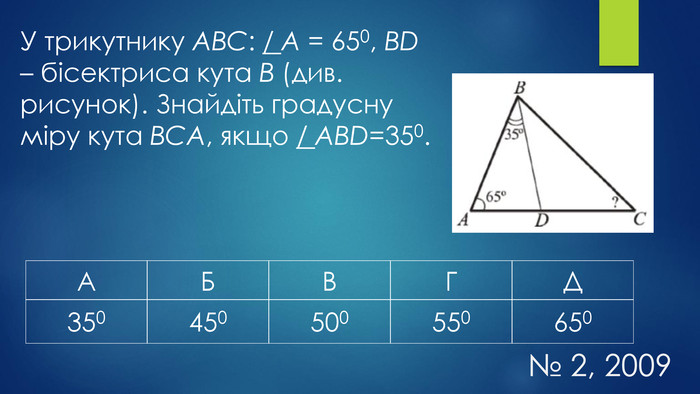



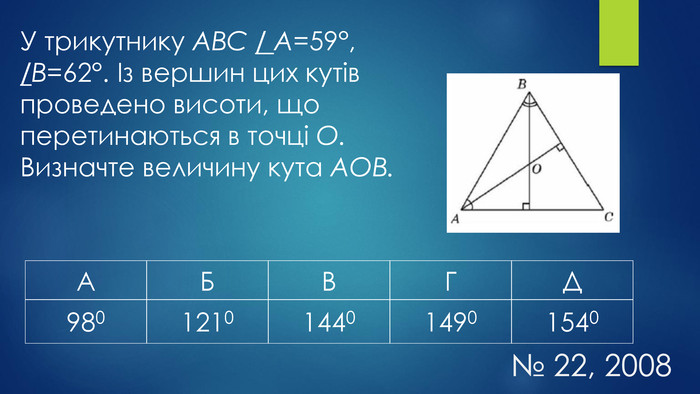

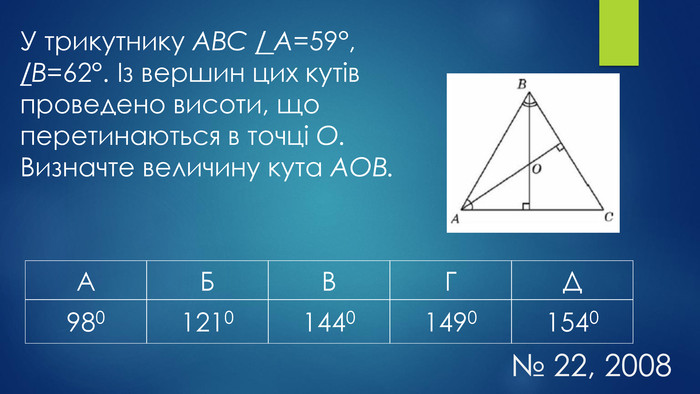



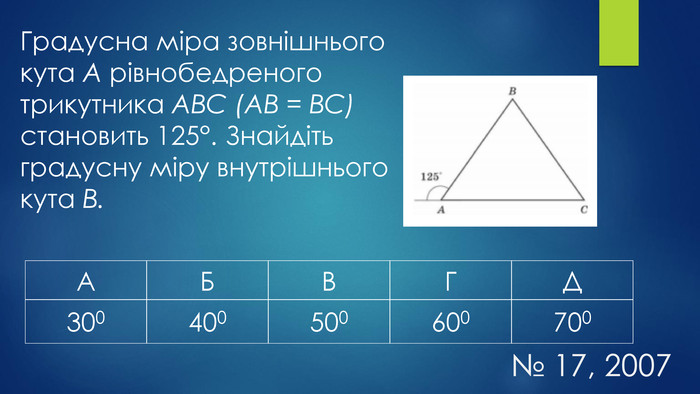














Мета уроку:навчальна: систематизувати, узагальнити знання учнів про трикутники та їх властивості, формувати вміння і навички розв’язувати задачі, користуючись означенням та властивостями трикутника;розвивальна: удосконалювати навички застосовувати властивості трикутників під час розв’язування задач, здатності до самостійного мислення, розвивати пам’ять, увагу;виховна: формувати працьовитість, прищеплювати бажання мати якісні, глибокі знання, виховувати культуру математичних записів та інтерес до вивчення предмету.
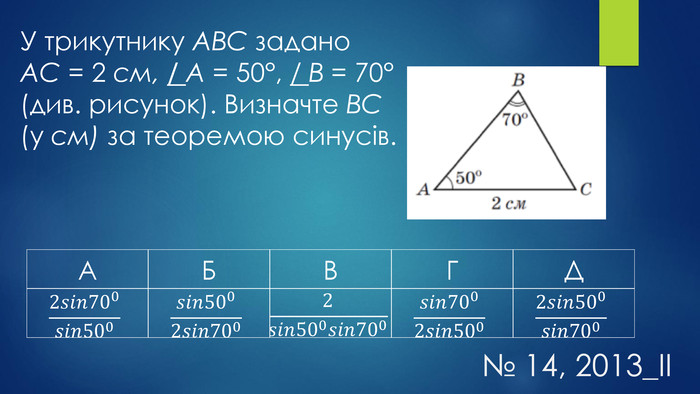
№ 14, 2013_ІІУ трикутнику ABC задано AC = 2 см, / А = 50°, / B = 70° (див. рисунок). Визначте ВС (у см) за теоремою синусів.{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД2𝑠𝑖𝑛700𝑠𝑖𝑛500𝑠𝑖𝑛5002𝑠𝑖𝑛7002𝑠𝑖𝑛500𝑠𝑖𝑛700𝑠𝑖𝑛7002𝑠𝑖𝑛5002𝑠𝑖𝑛500𝑠𝑖𝑛700{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД
№ 16, 2010_ІНа папері у клітинку зображено трикутник ABC, вершини якого збігаються з вершинами клітинок (див. рисунок). Знайдіть площу трикутника ABC, якщо кожна клітинка є квадратом зі стороною завдовжки 1 см{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД15 см28,5 см28 см27,5 см27 см2
№ 23, 2017д. Рівносторонній трикутник АВС та рівнобедрений трикутник ACD, у якому AC = DC і / ACD = 400, лежать в одній площині (див. рисунок). Установіть відповідність між кутом (1–4) та його градусною мірою (А–Д). Вираз Твердження про значення виразу1 / ABC А 4502 / ADC Б 5003 кут між прямими AB i AD В 6004 кут між бісектрисами Г 650кутів BAC і CAD Д 700
Розв’язання.1. / ABC =600 (трикутник АВС – рівносторонній).2. кут 𝐴𝐷𝐶=1800−4002=7003. кут 𝐵𝐴𝐷=600+700=1300 . Кут між прямими AB i AD дорівнює меншому з утворених кутів, тобто 1800 – 1300 = 5004. кут між бісектрисами кутів BAC і CAD рівний 12𝐵𝐴𝐷=121300=650 Відповідь: 1 – В, 2 – Д, 3 – Б, 4 – Г.
№ 23, 2017 У трикутнику АВС: АВ = с, ВС = а, АС = b. До кожного початку речення (1–4) та доберіть його закінчення (А–Д) так, щоб утворилося правильне твердження. Початок речення Закінчення речення1 Якщо 𝑎=𝑏=𝑐 А то / С = 3002 Якщо 𝑐2=𝑎2+𝑏2 Б то / С = 4503 Якщо 𝑎=𝑐=𝑏2 В то / С = 6004 Якщо 𝑐2=𝑎2+𝑏2−2𝑎𝑏∙−12 Г то / С = 900 Д то / С = 1200
Розв’язання.1. 𝑎=𝑏=𝑐. Отже, ΔАВС рівносторонній. Таким чином /С = 6002. 𝑐2=𝑎2+𝑏2. Виконується теорема Піфагора. Таким чином / С = 9003. 𝑎=𝑐=𝑏2. 𝑐1=𝑏2,𝑐𝑏=12. За теоремою синусів 𝑐sin450=𝑏sin900,𝑐𝑏=12. Таким чином / С = 4504. 𝑐2=𝑎2+𝑏2−2𝑎𝑏∙−12. Виконується теорема косинусів. Таким чином / С = 1200, оскільки cos1200=−12 Відповідь: 1 – В, 2 – Г, 3 – Б, 4 – Д.
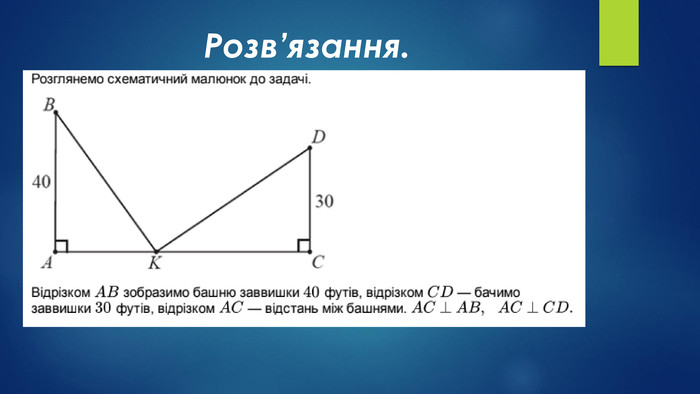
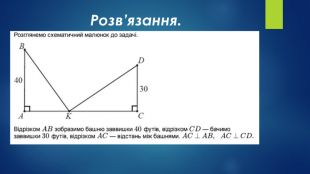
№ 24, 2006(Задача Л. Пізанського, XII—XIII ст.)Дві вежі, одна з яких – 40 футів, а друга – 30 футів заввишки, розташовано на відстані 50 футів одна від одної. До криниці, що знаходиться між ними, одночасно з обох веж злетіло по пташці. Рухаючись з однаковою швидкістю, вони прилетіли до криниці одночасно. Знайдіть відстань від криниці до найближчої вежі (у футах).


про публікацію авторської розробки
Додати розробку





















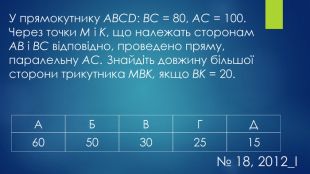







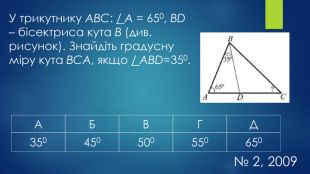



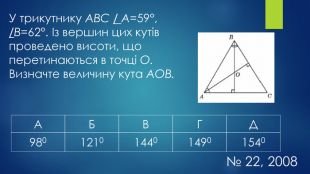

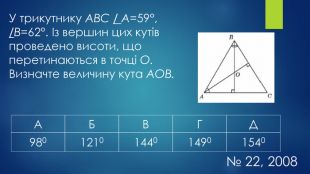




















-

Джерело tkd94846
05.04.2023 в 13:24
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
21.02.2023 в 16:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Личко Вікторія Михайлівна
23.01.2022 в 13:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прохорчук Тетяна Павлівна
26.03.2021 в 20:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Чубарь Елена
04.02.2021 в 01:25
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Новомлинська Дар'я Сергіївна
21.04.2020 в 22:24
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жолобанюк Оксана Дмитрівна
04.06.2018 в 19:07
Спасибі! Пропоную додати ще свої цікаві задачі з "родзинкою"!
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 4 відгука