Методичні рекомендації "Методика викладання задач професійного спрямування на уроках геометрії у професійно - технічному училищі"
Робота зі складеною системою прикладних стереометричних задач виступає ефективним засобом активізації пізнавальної діяльності старшокласників. Запропонованаметодика реалізації прикладної спрямованості узгоджується із віковими, психологічними особливостями учнів старшої школи,враховує окремі ідеї диференціації навчання: профіль навчальної групи, рівень навченості конкретного учня. Це проявляється на підготовчійта початковій (мотивація навчальної діяльності) стадіях реалізації даної методики; на основній стадії у процесі відбору тематики прикладних задач із створеної системи (технічні задачі, історичні тощо).
Методика реалізації прикладної спрямованості курсу стереометріїдозволяє легко поєднуватись із пануючою традиційною системою навчання .Вона сприяє підвищенню якості математичної підготовки учнів, посилює їх пізнавальну діяльність, допомагає подолати формалізм у навчанні, формувати позитивні мотиви навчальної діяльності та, як наслідок, сприяє досягненню учнями практичної компетентності, яка свідчить про готовність молоді до повсякденного життя, найважливіших видів суспільної діяльності, оволодіння майбутньою професією.
1
Державний навчальний заклад
«Нововолинський центр професійно-технічної освіти»
Методика викладання задач професійного спрямування на уроках геометрії
у професійно - технічному училищі
Панас Г.І.
Викладач математики
ЗМІСТ
Вступ ……………………………………………………………………………………………………. 3
І. Поняття прикладної спрямованості курсу стереометрії ………………………………………….. 6
1.1. Історичний аспект прикладної орієнтації курсу математики………………………………….. 6
1.2 Прикладна спрямованість шкільного курсу стереометрії……………………………………… 9
1.3. Педагогічні можливості прикладних задач у формуванні життєво важливих компетентностей учнів …………………………………………………………………………………………………… 14
1.3.1. Практична компетентність як показник якості математичної освіти …………………14
1. 3.2. Шляхи реалізації практичного спрямування курсу стереометрії………………………. 20
1.3.3. Інтеграція стереометрії з іншими навчальними предметами ………………………….. 27
1.3.4. Розв’язування прикладних задач методом математичного моделювання…………….. 30
ІІ. Методичні рекомендації щодо реалізації професійної спрямованості стереометрії у професійно- технічних навчальних закладах……………………………………………………………………… 34
2.1. Використання дидактичних матеріалів з професійною направленістю……………….. 34
2.2. Прикладна спрямованість матеріалу, пов’язаного із вивченням многогранників……. 45
2.3. Прикладна направленість матеріалу, пов’язаного із вивченням тіл обертання………. 55
Висновки ………………………………………………………………………………………………. 66
Список використаних джерел………………………………………………………………………… 69
Додатки………………………………………………………………………………………………… 71
ВСТУП
Дуже корисно пізнати справжнє виникнення чудових відкриттів, особливо таких, що були зроблені
не випадково , а силою думки. Це приносить користь
не стільки тим, що історія воздає кожному своє і спонукає інших добиватися таких самих похвал,
стільки тим, що пізнання методу на видатних
прикладах веде до розвитку мистецтва відкриття
Г.Лейбніц
Сучасне суспільство знаходиться у стані політичних та економічних змін. Тому для людини важливими є здатність бути мобільною та адаптивною, вміння бачити проблему, чітко формулювати та всебічно підходити до її розв’язування, здобувати необхідну інформацію тощо. Відповідно до потреб продукуються зміни в освіті, проходить її модернізація.
Національна доктрина розвитку освіти в Україні у ХХІ столітті вже зорієнтована на нове соціальне замовлення. Державний стандарт базової та повної середньої освіти визначає як основну мету освітньої галузі «Математика» опанування учнями системою математичних знань, навичок та умінь, необхідних у повсякденному житті та майбутній трудовій діяльності , достатніх для успішного оволодіння іншими освітніми галузями знань і забезпечення неперервної освіти; формування в учнів наукового світогляду, уявлень про ідеї та методи математики , про її роль у пізнанні дійсності, інтелектуальний розвиток учнів. Концепція математичної освіти школи визначає одним із пріоритетів розвитку математичної освіти необхідність посилення прикладної спрямованості математики. Важливість її реалізації підкреслено в пояснювальних записках до програм з математики для 11-річної школи.
Проблема реалізації прикладної спрямованості завжди була і є в полі зору методистів, науковців, авторів підручників. У роботах науковців проведено теоретичне обґрунтування її існування та шляхи розв’язування. Сформульовані загальні принципи, які забезпечують шкільному курсу математики прикладну спрямованість, розроблені шляхи розв’язування завдань навчання учнів застосовувати математичні знання на практиці, визначені умови реалізації прикладної спрямованості математики у навчальних закладах.
Прикладну спрямованість розглядають як засіб активізації навчально-пізнавальної діяльності учнів, виокремлюють як одну із функцій навчання, підкреслюють її важливість для формування мотивації навчання. Частина наукових досліджень присвячена проблемі формування в учнів умінь, пов’язаних із застосуванням математики, методиці прикладної спрямованості предметів шкільної математики, зокрема стереометрії. У значній кількості досліджень увага приділяється комплексному використанню засобів прикладної спрямованості : прикладних задач та інформації про походження математичних об’єктів.
Для вирішення даної проблеми важливим є формування в учнів прийомів діяльності прикладного характеру, моделювання в навчальній діяльності, використання інформаційно-комунікативних технологій, навчання учнів розв’язуванню прикладних задач, формування геометричного бачення світу, використання міжпредметних зв’язків.
Варто досліджувати прикладну спрямованість стереометрії, так як її вивчення має вагоме значення для інтелектуального розвитку людини та водночас на існуючі проблеми геометричної освіти у шкільній практиці.
Система освіти в нашій країні вступила в період фундаментальних змін, що характеризуються новим розумінням цілей освіти, новими концептуальними підходами до розробки і використання навчальних технологій і т. ін. Тому поставлені перед навчальними закладами завдання щодо поєднання навчання з подальшою продуктивною працею, підвищення ефективності навчання можуть бути реалізовані за умовами зміни відношення педагогів до навчального процесу, а саме підвищення математичної освіти за умов посилення її прикладного, практичного та політехнічного спрямування.
Нові суспільні умови та нові завдання освітньої галузі «математика» потребують корекції існуючих шляхів досягнення мети та вирішення зазначеної проблеми курсу математики. У навчальних закладах треба раз і назавжди відмовитися від технократичного мислення, коли засоби переважають над метою, коли на учня дивляться як на об’єкт маніпуляцій, який навчають або програмують, а не як на особистість з безліччю ступенів свободи її інтелекту.
Таким чином, актуальність проблеми обумовлена необхідністю у прикладній спрямованості змісту курсу «математика», а саме з демонстрацією та реалізацією її світоглядних і соціально - педагогічних функцій.
Активізація пізнавальної діяльності учнів – одна з гострих проблем, над вирішенням якої у даний час працює методична наука й національна школа.. Це зумовлено різким падінням соціального статусу і престижу знань серед молоді. Тут, як у фокусі, тісно переплітаються соціальні психолого-педагогічні та методичні проблеми виховання особистості на сучасному етапі розвитку суспільства.
Важливою стороною проблеми активізації навчально-пізнавальної діяльності є насамперед соціальний аспект. У національній державній програмі « Освіта» (Україна ХХ1 століття) зазначено, що загальна середня освіта має забезпечувати продовження всебічного розвитку дитини як цілісної особистості її здібностей і обдаровань, збагачення на цій основі інтелектуального потенціалу народу, його духовності та культури, формування громадянина України, здатного до свідомого суспільного вибору. Потяг до знань, високу пізнавальну активність та уміння самовдосконалюватися необхідно розвивати й виховувати у молоді під час навчання у професійних навчальних закладах. Успішне вирішення цього завдання щонайперше створює надійні передумови для глибокого та міцного оволодіння навчальним матеріалом. Разом з цим воно забезпечує умови для наступної систематичної роботи учнів над собою, для практичної реалізації ідеї неперервної освіти і самоосвіти.
Велике значення мають також психологічні і педагогічні передумови вирішення зазначеної проблеми. Оновлення змісту освіти, приведення його у відповідність із сучасними потребами особи і суспільства вимагає вдосконалення процесу навчання. У системі навчальних занять широке застосування мають знайти найбільш ефективні методи і прийоми організації навчання учнів, що сприятимуть збудженню і розвитку в них пізнавальної активності. Учень не зможе усвідомити і зробити власним надбанням матеріал, що вивчається, якщо він не відчуває потреби в його вивченні, і не виявлятиме розумової напруги, наполегливості в навчанні. Ось чому все більшого значення набуває орієнтація на розвиток учнів шляхом створення умов для широкого аналізу фактів, на озброєння умінням самостійно працювати, вчитися самому. Проте розвиток пізнавальної активності учнів відіграє велику роль не тільки у підвищенні рівня розвитку учнів і поліпшенні якості успішності, а і в їх вихованні. Адже перетворення знань на переконання і розвиток моральної свідомості учнів досягається лише тоді, коли учні всебічно усвідомлюють матеріал, що вивчається, коли засвоєні висновки й узагальнення є результатом їхніх власних розумових зусиль і позитивних емоційних переживань. Таким чином, сам підхід до навчання і методика його організації суттєво впливають на формування інтелекту, світогляду та морального обличчя учнів.
Психологи, дидакти та методисти одностайно вважають, що учнів необхідно спеціально навчати вміння поєднувати теоретичні знання з практичними діями. При цьому включення у процес навчання питань і задач прикладного та професійного змісту є лише необхідною умовою такого навчання. Крім цього, необхідно навчати учнів спеціальних прийомів розумової роботи, що є необхідними для застосування теоретичних знань, і формувати в них практичні вміння і навички, що лежать в основі застосування математики на інших уроках, у виробництві та побуті, у майбутній професії. Проблема застосування знань на практиці вимагає формування в учнів уміння аналізувати й синтезувати ситуації, конкретизувати загальні абстрактні положення, пізнавати відомі фігури, залежності у конкретних ситуаціях, переусвідомлювати один і той самий об’єкт або явище під кутом зору різних систем знань, варіювати способи дій, переключатися з одного виду діяльності на інший.
.
І. Поняття прикладної спрямованості курсу стереометрії
1.1. Історичний аспект прикладної орієнтації курсу математики
Однією з характерних особливостей нашого часу є широке застосування математики у різних галузях діяльності людини. Без математики не обійтися при проектуванні та будівництві споруд, виробництві приладів та їхніх деталей, важливу роль відіграє ця наука у плануванні господарчої діяльності, керуванні технологічними процесами, роботою підприємств.
Суттєве прискорення процесу математизації науки, техніки, господарської діяльності розпочалося в середині ХХ століття. Воно пов’язане зі створенням електронно-обчислювальних машин, автоматизацією процесів виробництва, новітніми технологіями, істотними змінами у характері праці людини.
Математика стала універсальним засобом моделювання та дослідження навколишнього світу, надійним знаряддям розв’язування практичних задач. Тому вивчення математики, її застосувань є невід’ємною складовою формування світогляду людини та підготовка сучасного фахівця – кваліфікованого робітника, техніка, інженера.
Очевидно, математика виникла на ранній стадії розвитку людства під впливом потреб практики. Розвиток ремесла, землеробства, торгівлі й обміну, навігації, управління державою потребував удосконалення вимірювань і розрахунків.
Неможливо точно відповісти на запитання , коли саме було сформовано перші математичні поняття.
Є переконливі писемні свідчення , які підтверджують високий рівень математичних знань у могутніх цивілізацій Стародавнього Сходу – Єгипті та Вавилоні – за три-дві тисячі років до н.е. Тогочасна математика мала яскраво виражений конкретний характер. Її досягнення дійшли до нас у вигляді задач, більшість з яких належить до розряду господарських, і їхніх розв’язків. У них ідеться про вимірювання площ і об’ємів, про обчислення.
Приблизно у VII ст. до н.е. виникла грецька цивілізація, яка відрізнялася від країн Стародавнього Сходу політичним ладом і економікою. Розквіт науки і мистецтва у Стародавній Греції супроводжувався плідними теоретичними дослідженнями. Намагання стародавніх греків зрозуміти будову Всесвіту, визначити роль і місце людини у природі та суспільстві привели до утвердження нових форм раціонального мислення. У математиці ця форма мислення виявлялась у прагненні людини довести всі твердження, виходячи з невеликої кількості початкових тверджень
У Стародавній Греції були зроблені відкриття , які на багато століть визначили напрямки розвитку математики. Поряд із досягненнями теоретичного характеру тогочасні вчені мали багато суто практичних здобутків. Найвидатнішим представником прикладної математики того часу історики вважають Архімеда (приблизно 187-212р.р. до н.е.). Він був не тільки математиком, а й талановитим інженером. Його праці з обчислення площ і об’ємів стали передвісниками найпотужніших сучасних методів математики.
З часом математичні дослідження на Сході мали арифметико-алгебраїчний характер і були більш прикладними, ніж за часів античності.
У той час , як Схід продовжував розвиватися, Західна Європа поступово занепадала. Та вже на початку ХІІ ст.. економічне життя Заходу активізується, пожвавлюється інтерес до математики. Математика стає важливим засобом наукового Відродження. Вчені змушені дбати про створення відповідного математичного апарату.
У ХVІІІ і ХІХ століттях розвиток математики був тісно пов'язаний із технічною революцією, вимогами практики.
З часом безпосередній вплив практики на розвиток математики дещо зменшувався. Однак становлення різних природничих і технічних наук було тісно пов’язане з удосконаленням математичних методів, розширення сфери їхнього застосування.
Важливим джерелом розвитку математики є її внутрішні потреби, спрямовані на систематизацію теорій, їхнє узагальнення, вдосконалення наукових методів.
Розвиток математики у ХІХ ст. визначався як її внутрішніми потребами так і потребами практики. Нерідко абстрактні математичні теорії з часом ставали прикладними.
Ще більшу роль у вивченні навколишнього світу і у суспільстві відіграє математика в ХХ ст.. Її можливості істотно зросли внаслідок створення електронно-обчислювальних машин. Сучасний етап розвитку суспільства характеризується значним ростом сфер застосування математики. Математика послуговується досить загальними і чіткими об’єктами для описання навколишніх явищ; вченими розроблено низку потужних методів дослідження математичних об’єктів.
Таким чином , математика є зручним і ефективним засобом для описання і дослідження закономірностей реальності.
Історизм у викладанні математики та її прикладна спрямованість тісно пов’язані. Більшість понять класичної математики зобов’язані своїм виникненням практичним потребам людини.
Про роль науки дуже влучно сказав Г.Лейбніц : «Дуже корисно пізнати справжнє виникнення чудових відкриттів, особливо таких, що були зроблені не випадково , а силою думки. Це приносить користь не стільки тим, що історія воздає кожному своє і спонукає інших добиватися таких самих похвал, стільки тим, що пізнання методу на видатних прикладах веде до розвитку мистецтва відкриття».
Усім відомий історичний факт відкриття у 1846р. невідомої до того часу планети Нептун. Її орбіту обчислили незалежно один від одного вчені Адамс І Левер’є. Відкриття планети «на кінчику пера» сприяло зростанню довіри до математики та створеної з її допомогою наукової картини світу.
Пошуки розв’язків окремих прикладних задач спонукали вчених розробляти нові методи досліджень, створювати досконаліші алгоритми, відкривати невідомі закономірності, що, у свою чергу, сприяло розвитку математичної науки.
Звернення до конкретних фактів з історії розвитку математики та вивчення математичних об’єктів розкриває практичний зміст математичних понять, пробуджує пізнавальний інтерес учнів до науки.
Історія розвитку математики дає змогу зрозуміти закономірності становлення математичного моделювання та його значення в пізнанні світу.
Моделювання в математиці почалося разом з її формуванням. У період, коли формувалися початкові математичні поняття та уявлення, відбувалося переважно накопичення математичних абстракцій, панували найпростіші математичні операції. Серед перших математичних систем найвідомішою є геометрія Евкліда, практичне походження якої не викликає сумніву. Евклідова геометрія – один з ранніх прикладів того, що математичні моделі, виникнувши, стають відносно самостійними й вивчаються у математиці незалежно від кола задач, що зумовили їх створення.
Історизм у викладанні математики та її професійна спрямованість тісно пов’язані. Більшість понять класичної математики зобов’язані своїм виникненням практичним потребам людини.
Пошуки розв’язків окремих прикладних задач спонукали вчених розробляти нові методи досліджень, створювати досконаліші алгоритми, відкривати невідомі закономірності, що, у свою чергу, сприяло розвитку математичної науки.
Звернення до конкретних фактів з історії розвитку математики та вивчення математичних об’єктів розкриває практичний зміст математичних понять, пробуджує пізнавальний інтерес учнів до науки.
1.2. Прикладна спрямованість шкільного курсу стереометрії
Роль математики в системі шкільної освіти істотно зростає в добу реформування системи шкільної освіти, що характеризується новим розумінням цілей навчання та новими підходами до розробки і використання освітніх технологій. Щоб бути успішним у сучасному складному мінливому суспільному житті, кожній людині необхідно бути мобільною, адаптивною; вміти бачити проблему, чітко формулювати та всебічно підходити до її розв’язування; здобувати необхідну інформацію тощо.
Особливості дитини її потреби та інтереси – це пріоритетні питання, які наразі повинні турбувати суспільство. Тому головна мета – зробити навчання і його результати корисними для учнів і нині і в майбутньому.
Державний стандарт базової та повної середньої освіти основними цілями освітньої галузі «Математика» визначає:
- опанування учнями системи математичних знань, умінь та навичок, необхідних у повсякденному житті та майбутній професійній діяльності, достатніх для успішного оволодіння на сучасному рівні предметів природничо-наукового та гуманітарного циклів, забезпечення неперервної освіти протягом життя;
- формування в учнів наукового світогляду, уявлень про ідеї та методи математики, про її роль у пізнанні дійсності;
- інтелектуальний розвиток учнів.
Реалізувати поставлені завдання можна за умови посилення практичної, прикладної та політехнічної спрямованості шкільного курсу математики.
Практичне спрямування передбачає формування в учнів умінь та навичок безпосередньо застосовувати здобуті знання під час вивчення теоретичного курсу математики.
Прикладне спрямування забезпечує вміння учнів використовувати здобуті під час вивчення математики знання в практичній діяльності (дослідженні реальних явищ, складанні математичних моделей задач та зіставленні отриманих результатів з реальними) та при вивченні природничих наук (фізики, біології, географії, астрономії, хімії).
Політехнічна направленість навчання передбачає використання математичних знань і вмінь у розв’язуванні задач, зміст яких пов'язаний із описом виробничих циклів, процесів обслуговування та керування.
Ідеться про реалізацію прикладної спрямованості курсу математики . Численні науково-методичні публікації свідчать про важливість цього напрямку у викладанні математики в навчальних закладах.
Прикладна спрямованість математичних наук – це змістовний та методологічний зв'язок курсу із практикою, що передбачає формування в учнів умінь, необхідних для розв’язування засобами математики практичних задач.
У педагогічних дослідженнях прикладну спрямованість математики розуміють як змістовний та методологічний зв'язок шкільного курсу з практикою, що передбачає формування в учнів умінь, необхідних для розв'язування засобами математики практичних задач.
Існує необхідність так організовувати вивчення математики, щоб воно було корисним і водночас захоплюючим, цікавим. А це можливо шляхом подолання надмірної абстракції, через розкриття ролі математики в пізнанні навколишнього світу, через інтеграцію з іншими шкільними предметами та формування у такий спосіб цілісного, гармонійного світосприйняття дитини.
Треба, як найменше говорити про виховання, а здійснювати вплив на формування особистості учня логікою предмету, і , що є найважливішим, прикладною спрямованістю змісту курсу «математика» з демонстрацією та реалізацією її світоглядних і соціально-педагогічних функцій.
Поставлені завдання щодо поєднання навчання з подальшою продуктивною працею, підвищення ефективності навчання можуть бути реалізовані за умови зміни відношення педагогів до навчального процесу.
Рівень і якість математичної освіти можна поліпшити підсиленням її прикладного, практичного та політехнічного спрямування.
Одним із дієвих та ефективних засобів реалізації прикладної спрямованості курсу математики є використання в навчальному процесі прикладних задач, які виникли в інших галузях, але потребують математичного розв’язання.
Прикладна задача повинна відповідати таким вимогам:
- питання задачі формулюється так, як воно зазвичай формулюється у житті;
- розв’язок задачі демонструє практичне застосування математичних ідей у різних галузях;
- зміст задачі повинен викликати в учнів пізнавальний інтерес;
- дані та шукані величини задачі мають бути реальними, узятими з життя.
Розв’язування прикладних задач у шкільному курсі математики сприяє ознайомленню учнів із роботою підприємств і галузей народного господарства, викликає інтерес до різних професій. Використання прикладних задач дає можливість вдало створювати проблемні ситуації на уроці .
Такі задачі забезпечують посилення мотивації навчання математики, спонукають учнів до здобуття нових знань, оволодіння новими вміннями, збагачують їх знаннями з інших дисциплін спеціального професійного циклу.
Відомо, що ефективним є також навчання, яке в єдності з вихованням забезпечує активізацію мислення учнів і свідоме засвоєння ними системи наукових знань, спонукає у них бажання та потребу в цих знаннях і викликає інтерес до предмета, допомагає розвитку здібностей кожного учня, розвиває вміння та навички застосовувати отримані знання на практиці, а також самостійно здобувати ці знання.
Підвищенню ефективності навчання математики сприяє розв'язування задач практичного змісту. Звернення до прикладів із життя і навколишньої дійсності полегшує вчителю організацію цілеспрямованої навчальної діяльності учнів.
У педагогічній літературі поняття прикладної задачі трактується по-різному, а саме як:
- задача, що потребує перекладу з природної мови на математичну;
- задача, яка близька за формулюванням і методами розв'язування до задач, що виникають на практиці;
- сюжетна задача, сформульована у вигляді задачі-проблеми.
Прикладна задача повинна задовольняти такі умови:
- питання задачі формулюється так, як воно зазвичай формулюється у житті;
- розв'язок задачі має практичну значимість;
- дані та шукані величини задачі мають бути реальними, взятими з життя.
Кожна прикладна задача виконує різні функції, що за певних умов виступають явно або приховано.
У методиці навчання математики існують різні тлумачення поняття “прикладна спрямованість”. Ю.М. Налягін і В.В. Пікан розрізняють поняття “прикладна” і “практична” спрямованість. Вони вважають, що прикладна спрямованість навчання математики – це орієнтація змісту і методів навчання на застосування математики в техніці і суміжних науках; у професійній діяльності; в народному господарстві і побуті .
Згідно з таким тлумаченням міжпредметні зв’язки, політехнічна спрямованість охоплюються потінням “прикладна спрямованість”.
Прикладна спрямованість сприяє формуванню наукового світогляду і показує роль математики в cучасному виробництві, економіці, науці.
Практична спрямованість навчання математики – це спрямованість змісту і методів навчання на розв’язування задач і вправ, на формування у школярів навичок самостійної діяльності математичного характеру .
У реальному процесі навчання прикладна і практична спрямованість звичайно функціонують спільно.
Дещо інакше розуміємо прикладну спрямованість В.А. Долінгер. Він вважає, що прикладна спрямованість математичних знань повинна означати як їх практичне застосування, так і їх теоретичне значення в самій математиці. Лише в цьому випадку буде виховуватися в учнів справжня повага до сили наукових знань .
Прикладна спрямованість навчання математики найбільше реалізується при розв’язування прикладних задач. Під прикладними задачами в школі здебільшого розуміють задачі, які виникають поза курсом математики і розв’язуються математичними методами і способами, які
визначаються в шкільному курсі.
Сформулюємо основні вимоги до прикладних задач, які використовуються у навчанні математики.
1. Задачі повинні мати реальний практичний зміст, який забезпечує ілюстрацію практичної
цінності і значущості набутих математичних знань.
2. Задачі повинні відповідати шкільним програмам і підручникам за формулюванням і змістом методів і фактів, які будуть використовувати в процесі їх розв’язування.
3. Задачі повинні бути сформульовані доступною і зрозумілою мовою, не містити термінів, з якими учні не зустрічалися і які вимагатимуть додаткових пояснень.
4. Числові дані в прикладних задачах повинні бути реальними, відповідати існуючим в практиці.
5. У змісті задачі по можливості повинен бути відображений особистий досвід учнів, місцевий матеріал, який дозволяє ефективно показати використання математичних знань і викликати в учнів пізнавальний інтерес.
6. Прикладні задачі повинні відображати ситуації промислового і сільськогосподарського виробництва, економіки, торгівлі, ілюструвати застосування математичних знань у конкретних професіях людей.
7. У прикладних задача числові дані, як правило, мають бути наближеними, а при їх розв’язуванні необхідно використовувати обчислювальні засоби, зокрема ЕОМ.
8. При розв’язанні прикладних задач їх формулювання може бути розширене і являти собою деяке теоретичне зведення до проблеми, що вивчається. Сама проблема може мати багатоступеневе розв’язання, при якому кожний наступний етап розвиває і доповнює попередній.
Сучасні проблеми часто неможливо вирішити з точки зору тільки однієї науки, необхідний комплексний підхід до розв’язування. Без математичного апарату не можуть існувати технічні науки, архітектура, економічні науки .
Мотивувати вивчення в навчальному закладі математики тим, що цей матеріал знадобиться у вузі, недоцільно – така мотивація буде дуже слабкою. А от показати, що набуті знання застосовуються для розв’язання задач з професійним змістом, розглянути задачу з іншого предмета – можливо.
Кожен учитель математики може перефразувати умову задачі так, щоб вона стала цікавою для учнів.
Серед задач з професійним змістом зустрічаються дуже складні. Вони не тільки мотивують вивчення певної теми та дозволяють застосувати знання, а й сприяють розвитку мислення учнів. Звісно, саме вивчення математики сприяє розвитку вміння логічно мислити, але розвиток буде більш швидким, якщо навчати учнів застосовувати різні прийоми мислення (аналіз, синтез, порівняння, узагальнення, конкретизування тощо).
Формування вмінь іі навичок застосування прийомів розумової діяльності здійснюється за етапами:
1. Знайомство учнів з окремими прийомами мислення при вивченні відповідного матеріалу.
2. Переконання в раціональності застосування даного прийому (не обтяжує, а полегшує розуміння матеріалу).
3. Визначення особливостей теми чи завдання, завдяки яким доцільно застосовувати саме цей прийом.
4. Навчання комплексному використанню різних прийомів мислення в різних комбінаціях.
5. Напрацювання звички самостійно застосовувати прийоми мислення. Для цього потрібно постійно нагадувати учням про доцільність тих чи інших дій, якщо вони самі забувають про це.
Відомо, що ефективним є також навчання, яке в єдності з вихованням забезпечує активізацію мислення учнів і свідоме засвоєння ними системи наукових знань, спонукає у них бажання та потребу в цих знаннях і викликає інтерес до предмета, допомагає розвитку здібностей кожного учня, розвиває вміння та навички застосовувати отримані знання на практиці, а також самостійно здобувати ці знання.
Отже прикладна спрямованість математики – це змістовний та методологічний зв'язок курсу із практикою, що передбачає формування в учнів умінь, необхідних для розв’язування засобами математики практичних задач.
1.3. Педагогічні можливості прикладних задач у формуванні життєво важливих компетентностей учнів
1.3.1.Практична компетентність як показник якості математичної освіти
Сучасні потреби розвитку України вимагають переходу на нову, більш гнучку, ніж існуюча, стратегію математичної освіти.
Вітчизняна освіта на сучасному етапі розвитку зазнає суттєвих змін: змінюються пріоритети, структура й зміст освіти, вводяться нові стандарти, формуються нові системи оцінювання результатів навчання. Відбувається процес оновлення шкільної освіти. Акцент переноситься на навчання, у процесі якого здійснюється формування і розвиток в учнів здатності практично діяти, застосовувати набуті знання і вміння до розв’язання життєвих проблем.
Новим концептуальним орієнтиром середньої освіти в країні є компетентно орієнтований підхід до формування змісту освіти, а також до організації навчально – виховного процесу.
Повернення школи до особистості учня виступає провідним принципом нового педагогічного мислення. І це не випадково. Суспільству потрібна компетентна, творча особистість, яка здатна брати активну участь у розвитку сучасного виробництва, економіки, науки та культури. Саме тому на перший план шкільної освіти виходить завдання створення оптимально сприятливих умов для виявлення і розвитку здібностей учнів, задоволення їхніх інтересів і потреб, розвиток навчально-пізнавальної активності та творчої самостійності.
Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності та навичками їх застосувань до розв’язання практичних задач. Значні вимоги до оволодіння математикою у розв’язання практичних задач ставлять сучасний ринок праці, отримання якісної професійної освіти, продовження освіти на наступних етапах. Тому основною вимогою є – досягнення кожним учнем практичної компетентності.
У сучасній педагогіці поступово встановлюється таке тлумачення понять:
компетенції – еталон досвіду дій, знань, умінь, навичок, творчості, який установлює суспільство;
компетентність – рівень досягнення компетенції;
компетентісний підхід – це спрямованість освітнього процесу на формування та розвиток життєвих (ключових) і предметних компетентностей особистості, результатом якого повинна бути сформована загальна компетентність людини, що є сукупністю життєвих компетентностей, інтегрованою характеристикою особистості.
Життєва компетентність на думку українських педагогів є об’єктивною категорією, яка фіксує cуспільновизнаний комплекс певного рівня знань, умінь і навичок, ставлень тощо, які можна застосовувати в широкій сфері діяльності людини.
Державний стандарт загальної освіти України визначає ключеві компетентності такі, як готовність учнів засвоєнні знання, уміння і навички використовувати для практичних завдань. Отже, головним завданням вчителя математики має бути не лише формування системи знань, умінь і навичок, а формування вмінь їх самостійно здобувати.
Варто сказати, що не існує єдиного узгодженого визначення та переліку ключових компетентностей.
Метою освітньої галузі "Математика" є формування предметної математичної і ключових компетентностей, необхідних для самореалізації учнів у швидкозмінному світі.
Для досягнення зазначеної мети передбачається формування:
- цілісного сприйняття світу, розуміння ролі математики у пізнанні дійсності; готовності до розпізнавання проблем, які розв'язуються із застосуванням математичних методів, здатності розв'язувати прикладні задачі, логічно міркувати, обґрунтовувати свої дії та виконувати дії за алгоритмом;
- вміння користуватися математичною термінологією і інформацією; орієнтуватися у просторі; застосовувати обчислювальні навички у практичних ситуаціях і розуміти сутність процесу вимірювання величин;
- інтересу до вивчення математики, творчого підходу та емоційно-ціннісного ставлення до виконання математичних завдань; уміння навчатися.
Такі об’єктивні чинники як науково-технічний прогрес, інформаційні технології, соціально-економічні зміни, зміна ринку праці, прагнення України до інтеграції у світове, європейське співтовариство впливають на особистість і вимагають від неї здатності вчитись все життя, оновлювати свої знання, самовдосконалюватись, інтелектуально зростати.
Усе це вивело в освіті на порядок денний питання формування в дитини життєвої компетентності.
Тому кожна людина повинна:
вміти:
працювати незалежно, самостійно розподіляти свій час, організовувати свою роботу,
користуватися джерелами інформації, вибирати необхідну інформацію;
мати:
почуття відповідальності, позитивну мотивацію до діяльності.
Компетентність - це знання, професіоналізм, високі моральні якості, вміння діяти адекватно у відповідних ситуаціях, застосовувати знання, беручи на себе відповідальність за певну діяльність. Для вчителів математики головним завданням є формування в учнів математичної компетентності, як складової життєвої компетентності.
Математично компетентний учень:
- володіє знаннями в межах програми, вміє розв’язувати типові задачі;
- усвідомлює зв’язок математики з іншими предметами;
- має розвинене мислення;
- вміє опрацьовувати інформацію, самостійно оволодівати знаннями;
- вміє працювати на комп’ютері.
Практична компетентність передбачає, що випускник загальноосвітнього навчального закладу:
- вміє будувати і досліджувати найпростіші математичні моделі реальних об’єктів, процесів і явищ, задач, пов’язаних з ними, за допомогою математичних об’єктів, відповідних математичних задач;
- вміє оволодівати необхідною оперативною інформацією для розуміння постановки математичної задачі, її характеру й особливостей; уточнювати вихідні дані, мету задачі, знаходити необхідну додаткову інформацію, засоби розв’язання задачі; переформульовувати задачу; розчленовувати задачі на складові, встановлювати зв’язки між ними, складати план розв’язання задачі; вибирати засоби розв’язання задачі, їх порівнювати і застосовувати оптимальні; перевіряти правильність розв’язання задачі; аналізувати та інтерпретувати отриманий результат, оцінювати його придатність із різних позицій; узагальнювати задачу, всебічно її розглядати; приймати рішення за результатами розв’язання задачі;
- володіє технікою обчислень, раціонально поєднуючи усні, письмові, інструментальні обчислення, зокрема наближені;
- вміє проектувати і здійснювати алгоритмічну та евристичну діяльність на математичному матеріалі;
- вміє працювати з формулами (розуміти змістове значення кожного елемента формули, знаходити їх числові значення при заданих значеннях змінних, виражати одну змінну через інші і т. п.).
Практична компетентність є важливим показником якості математичної освіти, природничої підготовки молоді. Вона певною мірою свідчить про готовність молоді до повсякденного життя, до найважливіших видів суспільної діяльності, до оволодіння професійною освітою.
Компетентність сьогодні трактується як інтелектуально й особистісно обумовлений життєвий досвід соціально-професійної життєдіяльності людини, який ґрунтується на знаннях, цінностях, нахилах, набутих підчас навчання.
Сьогодення вимагає чисельної армії вчених, винахідників, конструкторів не тільки для створення нових технічних систем, але й для грамотного обслуговування існуючих. Це є однією з умов виживання людства, захисту від техногенних катастроф.
Свою навчально-виховну діяльність вчитель повинен організувати так, щоб не лише дати учням певну кількість знань, умінь і навичок, але й сформувати математичну компетентність.
Предметна математична компетентність - особистісне утворення, що характеризує здатність учня створювати математичні моделі процесів навколишнього світу, застосовувати досвід математичної діяльності під час розв'язування навчально-пізнавальних і практично зорієнтованих задач.
Математична компетентність – уміння бачити й застосовувати математику у реальному житті, розуміти зміст і метод математичного моделювання, вміння будувати математичну модель, досліджувати її методами математики, інтерпретувати здобуті результати, обчислювати похибки обчислень. Досить далекими від математичної компетентності є запам’ятовування формул, уміння застосовувати готові схеми, розв’язування формальних задач; використання на побутовому рівні й описування за допомогою побутових термінів математичних понять. Математична компетентність будь-якого спеціаліста розглядається як обов’язків елемент загальної культури.
Для багатьох предметів математика є опорним курсом. Математика використовується для подання, систематизації й обробки інформації, отже, математична компетентність є органічною складовою професійної компетентності будь-якої особистості.
Розвиток математичної компетентності учня має бути системним і включати різні аспекти навчально-виховного процесу. Чільне місце в системі діяльності вчителя належить урокам. Саме на уроках учні здобувають важливі теоретичні знання з математики, вчаться застосовувати їх на практиці.
Математична освіта покликана зробити вагомий внесок у формування ключових компетентностей учнів як загальних цінностей, що базуються на знаннях, досвіді, здібностях, набутих завдяки навчанню. Отримані в школі знання та сформовані вміння і навички є, безперечно, важливими, але нині особливої актуальності набуває компетентність учня в різних галузях знань. Саме компетентності більшість міжнародних експертів вважають тими індикаторами, що дають змогу визначити готовність учня-випускника професійних технічних закладів до життя, подальшого особистого розвитку та активної участі в суспільному житті.
З точки зору компетентнісно зорієнтованого підходу до організації навчально-виховного процесу, зміст математичної освіти має бути спрямований на досягнення таких цілей:
- інтелектуальний розвиток учнів, формування видів мислення, характерних для математичної діяльності і необхідних людині для повноцінного життя у суспільстві;
- оволодіння прийомами математичної діяльності, які необхідні у вивченні суміжних предметів для продовження навчання та в практичній діяльності;
- формування уявлень про математику як форму опису і метод пізнання дійсності;
- виховання учнів у процесі навчання математики;
- формування позитивного ставлення та інтересу до математики.
Викладання математики має відображувати діалектику пізнання дійсності і побудови математичних теорій.
Математичні компетентності складають основу для формування ключових компетентностей. Математична компетентність – це спроможність особистості бачити та застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, будувати математичну модель, досліджувати її методами математики, інтерпретувати отримані результати, оцінювати похибку обчислень.
До математичних компетентностей відносяться такі:
- Процедурна компетентність – уміння розв’язувати типові математичні задачі.
- Логічна компетентність – володіння дедуктивним методом доведення та спростування тверджень.
- Технологічна компетентність – володіння сучасними математичними пакетами.
- Дослідницька компетентність – володіння методами дослідження практичних та прикладних задач математичними методами.
- Методологічна компетентність – уміння оцінювати доцільність використання математичних методів для розв’язування практичних та прикладних задач.
Природа компетентності така, що вона може проявлятися лише в органічній єдності з цінностями людини, тобто в умовах глибокої особистої зацікавленості в даному виді діяльності.
Компонентами математичної компетентності, як і будь-якої іншої, є:
- мотиваційний – внутрішня мотивація, інтерес;
- змістовний – комплекс математичних знань, умінь та навичок;
- дійовий – навички навчальної праці (самостійність, самооцінка, самоконтроль).
Формування мотиваційного компонента здійснюють через забезпечення позитивного ставлення учнів до математичної діяльності. Внутрішня мотивація у багатьох учнів ще нестійка і залежить від ситуації.
Під час вивчення курсу математики варто використовувати елементи історизму. Включення елементів історії розвитку науки, техніки дозволяє вирішувати низку педагогічних задач:
- підвищення інтересу до вивчення предмету;
- формування загальної культури учнів;
- формування наукового мислення;
- гуманістичне виховання.
Історичні екскурси можуть дати учневі повне уявлення про закономірності розвитку науки і техніки протягом історії людства, формування цивілізацій; сприяти розвитку його науково-технічного світогляду. Учень буде ознайомлений з основами сучасної науки, зрозуміє роль науки і техніки в житті, в розвитку матеріальної і духовної культури людства.
У математиці принцип історизму тісно пов’язаний із принципом прикладної спрямованості.
Щоб підготувати учнів до життя, суспільно-корисної праці викладачі повинні особливу увагу звертати на ті питання програми, з якими можуть зустрічатися їх вихованці в житті. В цьому полягають і практичні цілі навчання математики.
Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності і навичками їх застосувань до розв’язування прикладних задач. У процесі роботи над задачами такого типу здійснюється навчання учнів елементам математичного моделювання; вони не лише засвоюють найважливіші математичні поняття, але й відчувають взаємозв’язок теорії з практикою, усвідомлюють значення та необхідність вивчення теми, формують ключові компетентності. Прикладні задачі, особливо ті, які не втратили своєї актуальності впродовж століть, забезпечують гармонійну взаємодію учнів із суспільством.
Розв’язування з учнями задачі прикладного спрямування спрямоване на формування у них системи знань, умінь та навичок, робота з ними розвиває вміння осмислювати зміст понять та застосовувати здобуті знання на практиці, аналізувати результати, робити відповідні узагальнення, порівняння, висновки, розширює світогляд учнів.
Формування змістовного компоненту математичної компетентності здійснюється на основі індивідуально-диференційованого підходу. При цьому використовують різні форми організації навчальної діяльності учнів: індивідуальну, групову, фронтальну, роботу в парах.
Використання прикладних задач на уроках математики сприяє активізації міжпредметних зв’язків.
Таким чином, реалізуючи на уроках математики принципи історизму та прикладної спрямованості, вчитель досягає:
- опанування навичок застосування учнями базових математичних понять у контексті повсякденного життя та в процесі трудової діяльності;
- зростання інтересу школярів до вивчення математики і в цілому до навчання;
- розвитку духовних цінностей особистості: витонченості логічних міркувань, математичного мислення, повагу до вчених минулого;
- формування гуманістичної системи спілкування між учителем та учнями, перетворення кожної дитини на самостійно мислячу особистість, здатну поважати себе й інших.
1.3.2. Шляхи реалізації практичного спрямування курсу стереометрії
Серед напрямів, які можуть поліпшити рівень і якість шкільної математичної освіти, є підсилення її практичного і прикладного спрямування.
Практичне спрямування курсу математики передбачає вироблення в учнів умінь використовувати здобуті знання під час вивчення як самої математики, так і інших навчальних предметів, при цьому застосовувати раціональні обчислювальні прийоми; розв’язувати рівняння і нерівності, користуватися обчислювальною технікою тощо.
Прикладні задачі сприяють виконанню багатьох завдань навчального процесу. Крім попередньої підготовки учнів до свідомого дослідження реальних явищ природи, ці задачі дають можливість розкривати методологічні питання взаємозв’язку теорії і практики під час вивчення математики, формувати в учнів наукове світорозуміння. За їх допомогою вчителі можуть активізувати пізнавальну діяльність учнів, підвищити їх інтерес до навчального предмета.
Важливим фактором формування наукового світорозуміння є те, що різні математичні залежності створюються під впливом практики і практичних потреб людини.
Значну увагу варто присвятити прикладним задачам як одному із основних засобів реалізації прикладної спрямованості курсу стереометрії у школі. З огляду на існуючі у мовній практиці, науково-методичній літературі термінологічні розбіжності щодо поняття "прикладна задача", різні форми його визначення, уточнено таке. Задачі, які використовуються у навчальній діяльності, мають свою специфіку порівняно із задачами, що розв'язуються у науковій діяльності: мету використання, спосіб формулювання, засоби і оптимальність розв'язування, застосовність знайденого розв'язку тощо. Прикладними називаємо задачі, які виникають за межами математики, але розв'язування яких вимагає застосування математичного апарату. Прикладною задачею практичного характеру називатимемо задачу, розв'язування якої передбачає використання реального предмета (його виготовленої моделі), потребує проведення геометричного експерименту, відповідних вимірювальних робіт тощо. Прикладною задачею теоретичного характеру назвемо задачу, якщо її розв'язування не пов'язане з роботою із реальним предметом або його виготовленою моделлю. Також, залежно від вимоги, поряд із прикладними задачами на обчислення, побудову виділено якісні прикладні задачі. Це задачі із вимогою пояснити, дослідити або обґрунтувати певний факт або положення дійсності із можливим, але необов'язковим виконанням обчислень, побудов тощо. Цінність таких задач, неускладнених обчисленнями, у тому, що вони дозволяють зосередитись учням на ясному та точному з'ясуванні геометричної суті аксіом, постулатів, теорем, понять та уявлень; формують в учнів геометричне мислення та інтуїцію, розуміння процесу математичного моделювання.
Ідеться про реалізацію прикладної спрямованості курсу математики. Прикладна спрямованість математики – це змістовний та методологічний зв'язок курсу із практикою, що передбачає формування в учнів умінь, необхідних для розв’язування засобами математики практичних задач.
Для реалізації питання прикладної спрямованості шкільного курсу стереометрії побудована концептуальна модель.
Її структурними компонентами є цільовий (цілі, що сформульовані у прикладному напрямку), стимулюючо-мотиваційний, змістовий, операційно - діяльнісний, контрольно-оцінний.
Концептуальна модель передбачає також три функціональні компоненти. Перший – дії, пов’язані з мотивацією і постановкою цілей вивчення курсу, з’ясування учнями важливості прикладної складової та прикладного потенціалу абстрактної складової курсу стереометрії. Другий – навчальні дії: а) дії, що пов’язані із внесенням до навчання компонентів, характерних для прикладної діяльності; застосування математичного моделювання як основи вивчення курсу стереометрії та методу розв’язування прикладних задач; розвиток суто математичних вмінь та навичок , потрібних для розв’язування прикладних задач; б) дії, що притаманні професійно-навчальній діяльності: навички планування та корегування діяльності, самостійної роботи, творчої діяльності, роботи з комп’ютерними програмами; в) дії, пов’язані з моделюванням геометричних ситуацій та проведенням геометричного експерименту. Третій компонент – дії контролю та оцінювання знань.
Реалізація прикладної спрямованості починається із підготовчої стадії, на якій діяльність вчителя полягає у визначенні прикладно-орієнтованих цілей і планування навчальної діяльності з вивчення курсу стереометрії в конкретній навчальній групі. Її засобами є діюча програма; інформація про профіль, рівень научуваності, особливості навчальної групи; орієнтири дій із корекції планування у контексті прикладної спрямованості стереометрії та варіанти редакції цілей вивчення курсу, окремих розділів або тем.
На початковій стадії навчальна діяльність учителя безпосередньо корегується із навчальною діяльністю учнів у такий спосіб : а) розповідь вчителя про предмет стереометрії, метод, спосіб та організаційні засоби його вивчення, визначення стереометрії – сприймання учнями інформації, з’ясування ними початкових характеристик курсу, планування своєї навчальної діяльності; б) постановка вчителем цілей вивчення цього курсу – їх сприймання та усвідомлення учнями як особистісно значущих. Форма, в якій повинні бути визначені та сформульовані для учнів цілі вивчення курсу чи теми має бути рекламною. Для створення такої форми доцільно залучати комп’ютерно - комунікаційні технології. Важливо на цій стадії організувати спільну діяльність учителя та учня для з’ясування засобів досягнення поставлених цілей, аналізу можливих труднощів вивчення курсу стереометрії та способів їх подолання.
На підготовчій стадії основна робота відводиться вчителю (написання планів, створення дидактичного матеріалу, тощо).
На основній стадії реалізації прикладної спрямованості шкільного курсу геометрії діють найважливіші її засоби: 1) прикладна орієнтація абстрактної частини шкільної стереометрії, залучення прикладної інформації; 2) прикладні задачі; 3) засоби наочності; 4) комп’ютерно-комунікаційні технології. Доцільним є підводити прагматичний підсумок (систематично з’ясовувати разом з учнями особистісну цінність знань, умінь та навичок, що набуті за певний період вивчення курсу чи теми ).
Певна розроблена система є тим засобом, що допомагає вчителю формувати в учнів уміння виконувати загальні, спеціальні розумові дії, набувати учнями навички самостійної роботи. Це пояснюємо тим, що вона поєднує різноманітні задачі, що потребують проведення всіх або окремих етапів математичного моделювання; містять надлишкову або недостатню кількість даних для розв'язування; нерозкриту вимогу; дають можливість учням аналізувати інформацію з геометричної точки зору, усвідомлювати відмінності між об'єктом та його моделлю; формують в учнів поняття об'єму і площі поверхні та вміння їх правильно оцінювати, обчислювати; демонструють міжпредметні зв'язки та ін. Для ефективної організації навчальної діяльності учнів із розв'язування прикладних задач для вчителя визначено методичні прийоми та орієнтовні дії. Перед розв'язуванням прикладних задач доцільно: 1) з'ясувати із учнями, що таке прикладна задача, визначити етапи її розв'язування (на прикладі текстової задачі); 2) познайомити учнів із таблицею застарілих мір; 3) започаткувати ведення словника для полегшення перекладу умови прикладної задачі на мову математики (наприклад, місткість – об'єм); 4) з'ясувати доцільність додержання правил наближених обчислень під час розв'язування прикладних задач, нагадати ці правила учням. На етапі формалізації важливо: 1) використовувати евристичні запитання; 2) абстрагуватись від властивостей об'єкту, несуттєвих для побудови його моделі; 3) допомагати учням чітко вказувати відмінності між об'єктом та його моделлю, формулювати умову та вимогу прикладної задачі на мові математики. На етапі розв'язування задачі всередині побудованої моделі слід: 1) навчати учнів користуватись джерелами необхідних додаткових даних (проведення вимірювань; використання довідкової літератури) та теоретичних відомостей (підручники; тезово-опорні конспекти ); 2) вводити задачі-двійники (абстрактні задачі, розв'язування яких подібне до розв'язування прикладної задачі всередині побудованої моделі); 3) перед виконанням учнями рисунків до прикладних задач дозволяти їм виконувати відповідні ескізи; 4) систематично застосовувати інформаційно-комп'ютерні технології для виконання рисунків, проведення обчислень; 5) доводити знайдений розв'язок до числового значення або розрахункової формули. На етапі інтерпретації потрібно наголосити на необхідності здійснювати перевірку знайденого розв'язку на відповідність вимозі задачі. Також визначена орієнтовна схема дій для учнів із розв'язування прикладних задач.
Значну увагу приділено організації роботи зі складання прикладних задач: дослідження джерел сюжетів та кількісної інформації для створення прикладних задач; обробка, систематизація та зберігання числових даних; з'ясування із учнями вимог до прикладних задач.
Результати дослідження переконують, що систематичне створення учнями прикладних задач, дидактичних матеріалів на основі прикладної інформації та їх застосування у навчальному процесі (як і виважене використання бесід, наприклад, про естетику пропорцій у природі та мистецтві ) сприяє вихованню у старшокласників поваги до культуро-творчих традицій різних народів, підвищує екологічну культуру; допомагає здійснювати міжпредметні зв'язки , отже, сприяє прикладній спрямованості курсу.
За результатами педагогічного дослідження виділено аспекти використання моделей фігур: 1) демонстрація геометричного тіла з метою сприймати теоретичний матеріал і формувати математичні поняття; 2) ілюстрація окремих теоретичних положень; 3) спростування неправильних уявлень та покращення просторової уяви; 4) засіб вироблення окомірних навичок; 5) тренувальне поле для здійснення прямих та обернених операцій; 6) засіб показу взаємозв'язку, перетворення площинних та об'ємних фігур; 7) матеріал для проведення лабораторних робіт; 8) модель для рисунка просторової фігури; 9) унаочнення умови задачі; 10) основа для створення власної задачі; 11) допоміжний засіб учням під час контролю. Звичайно, що у такий спосіб можливо використовувати моделі, які виготовлені, наприклад, за допомогою розгорток.
На заключній стадії реалізації прикладної спрямованості шкільного курсу стереометрії діяльність вчителя полягає у здійсненні дій контролю, діяльність учня – у виконанні поставлених завдань та самоконтролю, спільної діяльності вчителя та учня – корегування, прогнозування подальшої навчальної діяльності.
Попередній контроль проводиться із діагностичною метою перед вивченням певного блоку матеріалу , за змістом – це поєднання прикладної та абстрактної складових. Поточний контроль здійснюється вчителем у ході навчальної діяльності на всіх ступенях вивчення . На третьому та четвертому ступенях вивчення має переважати письмова перевірки. Головна мета тематичного контролю – систематизація та узагальнення вивченого, діагностування якості засвоєння взаємозв'язків між структурними елементами навчального матеріалу відповідної теми , з'ясування розуміння прикладного значення матеріалу, який вивчається. У його контексті доцільно використовувати практичну перевірку (вона потребує застосування учнями своїх знань, вмінь та навичок для виконання завдань із моделями, реальними об'єктами). Під контролем вивчення розуміємо спільну діяльність учителя та учня, спрямовану на оцінювання та корекцію системності та систематичності знань про досліджувану у даній моделі та її властивості, вміння їх застосовувати до розв'язування прикладних задач . Підсумковий контроль проводять наприкінці кожного навчального семестру, року та курсу стереометрії. Його мета у контексті реалізації прикладної спрямованості стереометрії – встановити застосовність знань, умінь та навичок, набутих учнями для розв'язування навчальних завдань.
Таким чином, прикладна спрямованість шкільного курсу стереометрії – одна з цілей математичної освіти й основа , на якій опанування учнями математичних знань, умінь і навичок їх використовувати відбувається значно ефективніше. Забезпечення прикладної спрямованості сприяє формуванню стійких мотивів до навчання і до вивчення математики зокрема. Способи та засоби реалізації прикладної спрямованості у нових суспільних умовах та вимогах сьогодення до рівня, якості та характеру математичної освіти набувають актуальності за умови модернізації, уточнення та розширення. Побудована концептуальна модель та створена на її основі відповідна методика являються одним із варіантів реалізації прикладної спрямованості шкільного курсу стереометрії.
Формування навичок застосування математики є однією із головних цілей викладання математики. Радикальним засобом реалізації прикладної спрямованості шкільного курсу математики є широке систематичне застосування методу математичного моделювання протягом усього курсу. Це стосується введення понять, виявлення зв’язків між ними. Інакше кажучи, математики треба так навчати, щоб учні вміли її застосовувати. Забезпечення прикладної спрямованості викладання математики сприяє формуванню стійких мотивів до навчання взагалі і до навчання математики зокрема.
Вчителі протягом вивчення стереометрії приділяють увагу в основному опрацюванню теорії та розв’язуванню абстрактних задач, оскільки вони недооцінюють можливості реалізації прикладної спрямованості для досягнення цілей вивчення цього курсу. Посилюють цю ситуацію такі фактори: невелика кількість годин, що відведена для вивчення курсу стереометрії, у методичній літературі мало матеріалів, які доводять значущість прикладної спрямованості та конкретних методичних розробок , які допомагають вчителю використовувати її засоби. З огляду на перераховані обставини, у вчителів відсутня мотивація для систематичного прикладного спрямування курсу, зокрема для розв'язування з учнями прикладних задач, особливо враховуючи їх невелику кількість у підручниках, посібниках та майже повну відсутність серед добірок завдань контролюючого характеру.
У рамках визначеної проблеми вимагають вирішення у зв'язку із реформуванням освіти такі питання : створення концепції реалізації прикладної спрямованості, що враховує ідеї гуманітаризації освіти та вимоги диференціації навчання, обмеженість часового інтервалу, який відведено на вивчення стереометрії у школі; формування системи сучасних прикладних стереометричних задач, на базі якої можна навчити учнів спеціальних прийомів розумової діяльності і формувати практичні вміння, що лежать в основі застосування математики; використання інформаційно-комунікаційних технологій.
Таким чином, актуальність дослідження зумовлена соціальним запитом щодо прикладної спрямованості шкільного курсу стереометрії, необхідністю підвищення результативності його навчання та забезпечення інтелектуального розвитку учнів засобами геометрії, створення концепції реалізації прикладної спрямованості шкільного курсу стереометрії в сучасних умовах, потребами методичного оснащення процесу її реалізації.
Формування навичок застосування математики є однією із головних цілей викладання математики. Радикальним засобом реалізації прикладної спрямованості шкільного курсу математики є широке систематичне застосування методу математичного моделювання протягом усього курсу. Це стосується введення понять, виявлення зв’язків між ними. Інакше кажучи, математики треба так навчати, щоб учні вміли її застосовувати. Забезпечення прикладної спрямованості викладання математики сприяє формуванню стійких мотивів до навчання взагалі і до навчання математики зокрема.
Відомо, що ефективним є також навчання , яке в єдності з вихованням забезпечує активізацію мислення учнів і свідоме засвоєння ними системи наукових знань, спонукає у них бажання та потребу в цих знаннях і викликає інтерес до предмета, допомагає розвитку здібностей кожного учня, розвиває вміння та навички застосовувати отримані знання на практиці, а також самостійно здобувати ці знання. Підвищенню ефективності навчання математики сприяє розв’язування задач практичного змісту. Звернення до прикладів із життя і навколишньої дійсності полегшує вчителю організацію цілеспрямованої навчальної діяльності учнів.
Існує необхідність так організувати вивчення математики, щоб воно було корисним і водночас захоплюючим, цікавим. А це можливо шляхом подолання надмірної абстракції, через розкриття ролі математики в пізнанні навколишнього світу, через інтеграцію з іншими предметами та формування у такий спосіб цілісного, гармонійного світосприйняття учнів.
Суть прикладної спрямованості середньої математичної освіти полягає у здійсненні цілеспрямованого змістового і методологічного зв’язку шкільного курсу математики з практикою, що передбачає введення у шкільну математику специфічних відомостей, які характерні для дослідження прикладних проблем математичними методами. Розв’язання цього завдання не можливо досягнути лише шляхом насичення шкільного курсу математики новим прикладним змістом, але вимагає певної орієнтації курсу математики в цілому.
Розв’язування прикладних задач сприяє ознайомленню учнів з роботою підприємств і галузей народного господарства, що є умовою орієнтації інтересу учнів до певних професій. Використання прикладних задач дозволяє вдало створювати проблемні ситуації на уроках. Такі задачі стимулюють учнів до здобуття нових знань, збагачують учнів теоретичними знаннями з технічних дисциплін.
Прикладна спрямованість шкільного курсу стереометрії – це орієнтація цілей, змісту та засобів навчання стереометрії в напрямку набуття учнями в процесі математичного моделювання знань, умінь і навичок , які використовуватимуться ними у різних сферах життя.
1.3.3. Інтеграція математики з іншими навчальними предметами
Досвід показує, що інтегроване навчання, за якого матеріал доповнюється іншими напрямками, дає набагато кращий результат порівняно із традиційним вивченням предмету. Практична спрямованість дозволяє сформувати систему знань, розвиває здібності до їх перенесення в інші галузі, сприяє формуванню цілісного світогляду учня.
Математиці властива універсальна застосовність. Однак математика при цьому не може замінити методи і поняття тих конкретних наук, де її застосовують. У цьому сенсі вона має прикладний , підпорядкований характер. А тому доцільно узгодити в часі і за темпами вивчення програму з математики з програмами інших предметів, що використовують математичний апарат.
Цікавим і перспективним є такий спосіб демонстрації зв’язку математики з іншими науками, як проведення інтегрованих уроків. Вони допомагають знання сучасних учнів зробити ціліснішими, дозволяють позбутися ефекту «клаптикової ковдри», на них формується науковий світогляд. Такі уроки сприяють встановленню логічних зв’язків між предметами. Наприклад, уроки математики можна інтегрувати з уроками виробничого навчання в такому поєднанні : «Формули. Побудова креслень одягу», «Одиниці маси. Робота з харчовими продуктами. Приготування страв». Інтегровані уроки мають яскраво виражену прикладну спрямованість і тому викликають пізнавальний інтерес учнів.
Міжпредметні зв’язки – це засіб побудови цілісної системи навчання на основі спільності змісту знань і методів наукового пізнання. Проблема міжпредметних зв’язків пов’язана з раціональним використанням математичних знань у практичній діяльності людей, оскільки сфера застосування математики постійно поширюється.
Під час добору прикладних задач доцільно дотримуватися певних вимог. Задача має демонструвати практичне застосування математичних ідей і методів та ілюструвати матеріал, що вивчається на певному уроці, містити відомі або інтуїтивно зрозумілі учням поняття та терміни, а також реальні числові дані, що не ведуть до громіздких обчислень. За таких умов використання прикладної задачі, складеної на матеріалах суміжних предметів, може дати потрібний педагогічний ефект.
Відомо, що математика є мовою багатьох природничих наук. Зв'язок математики з іншими науками демонструють інтегровані уроки. Вони допомагають зробити знання учнів більш цілісними й системними. Такі уроки сприяють встановленню логічних зв’язків між предметами, мають яскраво виражену прикладну спрямованість, викликають пізнавальний інтерес учнів.
Ще одним засобом побудови цілісної системи навчання на основі спільності змісту знань і методів наукового пізнання є міжпредметні зв’язки. Вони активізують пізнавальну діяльність учнів, сприяють підвищенню рівня науковості та доступності, підвищенню якості знань та вмінь, створюють умови для всебічного розвитку особистості. Для успішної реалізації міжпредметних зв’язків на уроках і позакласних заходах учитель повинен орієнтуватися, для вивчення якого навчального предмета може стати у нагоді той чи інший математичний матеріал і чітко усвідомлювати, з якою метою і в якій формі встановлюється зв’язок.
Найбільш ефективним засобом навчання є міжпредметні пізнавальні задачі, для розв’язання яких потребується залучення знань із декількох предметів, їх перенесення та узагальнення. Такі задачі сприяють росту самостійності учнів у здійсненні (впровадженні) між предметних зв’язків , вмінню узагальнювати знання з різних предметів при вивченні загальних об’єктів і питань. Між предметні задачі можуть бути спрямовані на досягнення пізнавальної мети. Під час розв’язування таких задач учні не тільки навчаються застосовувати математичні знання, а й дістають деякі нові відомості . Одночасно учні набувають корисних навичок роботи з довідниками, навчаються самостійно знаходити потрібну інформацію в додатковій літературі.
Досвід показує, що інтегроване навчання, за якого матеріал доповнюється іншими напрямками, дає набагато кращий результат порівняно із традиційним вивченням предмету. Практична спрямованість дозволяє сформувати систему знань, розвиває здібності до їх перенесення в інші галузі, сприяє формуванню цілісного світогляду учня.Серед напрямів, які можуть поліпшити рівень і якість шкільної математичної освіти, є підсилення її практичного і прикладного спрямування.
Практичне спрямування курсу математики передбачає вироблення в учнів умінь використовувати здобуті знання під час вивчення як самої математики, так і інших навчальних предметів, при цьому застосовувати раціональні обчислювальні прийоми; розв’язувати рівняння і нерівності, користуватися обчислювальною технікою тощо.
Прикладні задачі сприяють виконанню багатьох завдань навчального процесу. Крім попередньої підготовки учнів до свідомого дослідження реальних явищ природи, ці задачі дають можливість розкривати методологічні питання взаємозв’язку теорії і практики під час вивчення математики, формувати в учнів наукове світорозуміння. За їх допомогою вчителі можуть активізувати пізнавальну діяльність учнів, підвищити їх інтерес до навчального предмета.
Важливим фактором формування наукового світорозуміння ї те, що математичні формули, теореми, різні залежності створюються під впливом практики і практичних потреб людини.
Одним із найважливіших засобів забезпечення прикладної спрямованості навчання математики є встановлення природних міжпредметних зв’язків математики з іншими предметами, у першу чергу, з природничими. Особливої уваги заслуговує встановлення тісних, взаємовигідних зв’язків між математикою та інформатикою – двома освітніми галузями, які є визначальними у підготовці особистості до життя у постіндустріальному, інформаційному суспільстві. Прикладна спрямованість математичної освіти суттєво підвищується завдяки впровадженню комп’ютерів у навчання математики.
Широке застосування комп’ютерів у навчанні математики доцільне для проведення математичних експериментів, практичних занять, інформаційного забезпечення, візуального інтерпретування математичної діяльності, проведення досліджень.
Варто використовувати комп’ютер (використання комп’ютерних презентацій). Досвід показує,що це дуже потужний засіб, який робить процес розв’язання прикладних задач більш ефективним , цікавим і результативним. Тому розв’язування прикладних задач з стереометрії з використанням комп’ютерних презентацій (як засобу) дозволяє:
- суттєво посилити і інтенсифікувати процес формування у учнів умінь застосовувати математичні знання на практиці , в нестандартних умовах;
- ефективно здійснювати міжпредметні зв’язки з іншими предметами;
- підвищувати практичну підготовку учнів по математиці, вчити їх вмінню володіти методом математичного моделювання;
- формувати в учнів наукову картину світу, позитивні мотиви до навчання, вміння бачити реальний світ через «математичні окуляри».
Створення систем гарних і змістовних прикладних задач, презентацій, ефективних методичних рекомендацій по їх розв’язуванню – широка методична проблема.
- Розв’язування прикладних задач методом математичного моделювання
Для успішної участі у суспільному житті особистість повинна володіти певними прийомами математичної діяльності та навиками їх застосувань до розв’язання конкретних практичних задач. Тому перед сучасною школою поставлені завдання щодо поєднання теоретичного навчання з подальшим практичним застосуванням, а саме підвищення шкільної математичної освіти за умов посилення її прикладного та практичного спрямування.
Прикладна спрямованість шкільного курсу математики як проблема, яку необхідно вирішити, та як завдання, яке потребує розв’язання у навчанні математики, задекларовані у різних освітніх документах, а саме в «Концепції загальної середньої освіти», «Державному стандарті базової шкільної середньої освіти: освітня галузь Математика», у програмах з математики для середньої школи та в інших документах .
Вперше означення поняття «прикладна спрямованість шкільного курсу математики» було запропоновано радянським педагогом-математиком В.В.Фірсовим. Згодом воно вдосконалювалось іншими вченими (Ю.М.Колягін, В.В.Пікан, З.І.Слєпкань, Г.П.Бевз). В найширшому розумінні сутність прикладної спрямованості шкільного курсу математики полягає в здійсненні цілеспрямованого, змістового та методологічного зв’язків математики з практикою та набуття учнями в процесі навчання математики знань, умінь і навичок, які будуть використовуватися ними в повсякденному житті, в навчанні, в майбутній професійній діяльності .
Основним методом реалізації прикладної спрямованості шкільного курсу математики є метод математичного моделювання, а найбільш ефективним засобом – прикладні задачі, розв’язування яких потребує глибоких знань як з математики,так і з інших дисциплін.
Усі наші знання про навколишній світ уявляються у вигляді найрізноманітніших моделей, серед яких є і математична.
Математичними моделями прийнято називати системи математичних об’єктів, що описують досліджуваний процес або явище математичною мовою. Для складання математичних моделей використовують різноманітні математичні засоби: рівняння, функції, графи, таблиці, геометричні конструкції тощо. У моделі концентрується сукупність наших знань, уявлень , гіпотез про відповідний об’єкт чи явище. Оскільки ці знання ніколи не бувають абсолютними, а гіпотези можуть іноді навмисне не враховувати деякі факти, то модель лише наближено описує поведінку реальної системи. Заміна вже наявних моделей на ті, в яких повніше відтворюються суттєві для дослідження властивості процесу чи явища, , комбіноване застосування різних моделей – шлях пізнання дійсності.
У процесі розв’язування прикладної задачі звичайно виникає потреба побудови математичних моделей реальних об’єктів, про які йдеться у задачі. Математичні моделі реального процесу або об’єкта можуть бути подані у вигляді формули, математичного малюнка, математичного твердження, геометричної фігури. У реальному житті є багато задач, які, на перший погляд , не мають між собою нічого спільного. Але часто для їх розв’язання можна використовувати одну й ту саму математичну модель. Отже, вміння працювати з однією математичною моделлю дає можливість розв’язувати різні прикладні задачі. Навчання учнів самостійно здійснювати дослідження, використовувати нестандартні підходи до розв’язування задач сприяє результативному та ефективному процесу формування творчого мислення учнів, підвищення навчально-пізнавальної діяльності.
Процесу розв’язування прикладної задачі властиві всі етапи математичного моделювання.
І етап. Створення математичної моделі – переклад задачі з природної мови тієї галузі, де вона виникла, на мову математики.
ІІ етап. Дослідження математичної моделі – на цьому етапі велика увага приділяється розробці алгоритму і методів розв’язування задачі, за допомогою яких результат можна знайти з необхідною точністю і за припустимий час. Тут важливу роль набувають математичний апарат, необхідний для аналізу та розв’язання математичної моделі.
ІІІ етап. Інтерпретація розв’язків – на цьому етапі з’ясовується , чи відповідають результати експерименту теоретичним наслідкам моделі в межах визначеної точності. Потрібно повернутися до початкової умови та з’ясувати, чи задовольняє одержаний розв’язок змісту прикладної задачі. Іноді в результаті такої інтерпретації з’ясовується, що розв’язки математичної задачі або не можуть бути розв’язками прикладної задачі, або виникає потреба в додаткових дослідженнях і перетвореннях.
У процесі розвитку науки і техніки дані про досліджувані явища усе більше і більше уточнюються і настає момент, коли висновки, що одержують на основі існуючої математичної моделі, не відповідають нашим знанням про явище. Таким чином, виникає необхідність побудови нової, досконалішої математичної моделі. Аналіз знайдених результатів обов’язків у процесі розв’язування прикладних задач.
Найбільш складним для учнів є перший етап. Це пов’язано з невмінням перекласти умову прикладної задачі на мову математики і створити адекватну математичну модель, оскільки у більшості учнів розвинуте алгоритмічне мислення, що є перешкодою розвитку творчого мислення. Якщо учням запропонувати готову модель прикладної задачі, або допомогти створити її, то з розв’язанням учні справляються добре. Проблеми також виникають в учнів на третьому етапі. Учні не завжди можуть проінтерпретувати розв’язок математичної задачі як розв’язок прикладної задачі. Отже, в учнів необхідно спеціально формувати вміння застосовувати теоретичні знання для розв’язання конкретних практичних задач.
Задачі прикладного характеру досить вдало доповнюють систему задач шкільного курсу математики і можуть використовуватися на різних етапах навчання і з різною метою. Залучення учнів до розв’язування таких задач на уроках математики сприяє розвитку творчого мислення, свідомому, якісному засвоєнню навчального матеріалу, активізує навчально-пізнавальну діяльність, дозволяє здійснювати перенесення отриманих знань і умінь в ту чи іншу галузь, що в свою чергу, активізує інтерес до завдань прикладного характеру і вивчення математики в цілому.
Застосування математики для описання і дослідження процесів та явищ дійсності ставить необхідність розглянути питання про сутність розв’язання прикладної задачі за допомогою математики. Певні процеси передбачають заміну реальних об’єктів і відношень між ними математичними об’єктами і відношеннями між ними. Для цього необхідно передусім виділити суттєві характеристики реальних об’єктів і відношень між ними, проігнорувавши несуттєві, а тоді – саме їх замінити математичними об’єктами і зв’язками між ними. Процес такого заміщення називають математичним моделюванням.
Математичними моделями звичайно називають наближені описання якогось класу явищ зовнішнього світу, виражені за допомогою математичних понять і відношень між ними.
Отже, процес математичного моделювання загалом складається з трьох етапів:
- вибір чи побудова математичної моделі для описання даної задачі;
- дослідження побудованої моделі, тобто розв’язування математичної задачі;
- тлумачення результатів дослідження , встановлення відповідності одержаного результату цілям досліджень.
При необхідності уточнюється сама математична модель і результати, які з неї випливають.
Метод математичного моделювання є потужним сучасним пізнавальним методом і ефективним засобом розв’язування прикладних задач. Роль його має стійку тенденцію до зростання у практичній діяльності.
- Прикладні математичні задачі підвищують мотивацію занять математикою. У процесі розв’язування таких задач зручно застосовувати математичні моделі.
- Багаторазове повторення ідей, методів і прийомів розв’язування задач методом математичного моделювання дає змогу залучити до начального процесу більшу частину учнів. Варто мати на увазі, що не всі однаково розвиваються в інтелектуальній сфері.
- Різноманітність підходів до розв’язування прикладних задач допомагає:
а) глибше осмислити математичні засоби;
б) продуктивніше розв’язувати задачі, що розвивають інтелект учня, гнучкість мислення.
- У методиці і практиці навчання математиці одні і ті самі задачі слід використовувати багаторазово, розв’язуючи їх кожного разу новими методами.
Побудова математичної моделі ґрунтується на абстрагуванні від властивостей об’єкта пізнання, крім кількісних і просторових. При побудові математичної моделі завжди виникає необхідність нехтувати тими чи іншими сторонами реальності. Про якість побудованої моделі можна судити лише за результатами порівняння дійсності з інформацією, отриманою шляхом дослідження моделі. Таким чином, метод математичного моделювання виходить з практики, створюючи математичні моделі явищ і процесів, і повертається до неї, щоб обґрунтувати доцільність створення моделі.
Застосування математики до розв’язування прикладних задач можна також зобразити за такою схемою: побудова математичної моделі → розв’язування математичної задачі → змістовий аналіз одержаних результатів.
Складність математичної моделі визначається складністю досліджуваного об’єкта й точністю розрахунків.
Зрозуміло, що цінність математики не зводиться тільки до вивчення певних явищ або процесів за допомогою моделей. Математика – це важлива наука, вона дає потужні методи для пізнання світу та вивчення його закономірностей.
Головна сила математики полягає в тому, що разом із розв’язуванням однієї конкретної задачі вона створює загальні прийоми та методи, що можуть бути застосовані в багатьох інших випадках, які не завжди можна передбачити.
Щоб з успіхом застосовувати математичні моделі необхідно передусім мати знання, вміти правильно користуватися математичним апаратом, знати межі допустимого використання математичної моделі, яка розглядається.
ІІ. Методичні рекомендації щодо реалізації професійної спрямованості стереометрії у професійно технічних навчальних закладах
2.1. Використання дидактичних матеріалів з професійною направленістю
Україні необхідні кваліфіковані спеціалісти, формування яких починається зі школи. Чільне місце у формуванні належить математиці, адже вона була і залишається технічною мовою для вивчення різних предметів.
Професійна направленість є одним із шляхів удосконалення математичної підготовки.
Завдання викладача математики професійно-технічного закладу – не просто дати знання учням з математики, а навчити як і де використовувати їх у майбутній професії.
У програмі з математики для професійно-технічних навчальних закладів викладено орієнтовні питання професійно-значущого матеріалу із стереометрії для окремих професій .
Знання з теми «Вступ до стереометрії» необхідні учням для просторової розмітки поверхонь,
розмітки і читанні електричних схем, виконання креслень моделей одягу, вивчення схем кінематичних схем.
Згідно програми учні повинні вміти:
- наносити паралельні лінії при розмітці,перевіряти горизонтальність поверхонь, деталей, правильність розміщення матеріалів та інструментів при виконанні робіт;
- використовувати властивості прямих і площин, паралельність при виконанні розмітки трас відкритих електропроводок, встановленні вимикачів, розеток, світильників, при виконанні креслень;
- наносити перпендикулярні лінії при розмітці, перевіряти вертикальність, правильність розміщення матеріалів та інструментів при виконанні робіт, визначати правильне розміщення поверхонь і інструментів у просторі.;
- розв’язувати виробничі задачі на обчислення площі основи, бічної та повної поверхні деталей та конструкцій (споруд), які мають форму многогранників, робити розрахунок матеріалів при виконанні робіт, визначати кути між поверхнями, інструментами.
Основними засобами реалізації професійної направленості на уроках математики є використання дидактичного матеріалу (питання, задачі, завдання професійного змісту).
Зміст дидактичних матеріалів, орієнтованих на зв’язок із професією, певним чином направляє пізнавальну діяльність учнів. Робота з такими матеріалами може сприяти формуванню в учнів вміння знаходити в професійній ситуації суттєві ознаки математичного поняття, використовувати це поняття в нових умовах.
Дидактичні матеріали можуть бути направлені на розвиток просторової уяви, обчислювальних навичок і графічних умінь, на розширення їх професійного кругозору, на формування загальнотрудових умінь і навичок роботи з вимірювальними приладами, таблицями , довідниками.
Навчальна задача повинна направити пізнавальну діяльність учнів на повторення опорних знань і способів дій, на осмислення значимості вивченого матеріалу для професії. Така задача направляє увагу учнів на розпізнання професійно значимого поняття або теоретичного твердження, на зв’язок і відношення між структурними одиницями поняття, твердження. Задача повинна бути націлена на обґрунтування того факту, що у виробничих ситуаціях існують об’єкти з властивостями математичних понять і операцій, які основані на теоретичних твердженнях; на становлення зв’язків і відношення даного професійно значимого визначення, теоретичного положення з іншими математичними знаннями і вміннями.
Деякі завдання можуть бути використані на кількох етапах уроку в залежності від різних умов: мети уроку, змісту математичного матеріалу, рівня математичної підготовки учнів, видів сучасного зв’язку між математичним і професійним матеріалом, вибраних форм навчання на уроці.
Так як дидактичний матеріал розробляється з врахуванням математичного і професійного змісту, то формулювання задачі повинне направляти пізнавальну діяльність на перенесення математичних знань на професійні, чи навпаки, професійних знань на математичний матеріал.
Виходячи з того, що математичний зміст тісно пов’язаний з професійним, при роботі з дидактичним матеріалом часто доводиться проводити порівняння, робити теоретичні обґрунтування, знаходити підтвердження теоретичним твердженням і поняттям в конкретній виробничій ситуації. Відповідною повинна бути і постановка задачі. Обов’язковими у її формулюванні являються вимоги: „порівняйте”, „обгрунтуйте”, „доведіть”, „знайдіть”, „визначте”, „наведіть приклади” і т.д., тобто слова-вказівки. Крім текстової частини часто у задачу входить предметна або зображувальна наочність. Це виражається у доповненні тексту графіком, таблицею, плакатом, діапозитивом, професійним інструментом, приладами, моделями виробничих об’єктів.
Певні дидактичні матеріали найкраще застосовуються на етапі формування умінь і навичок та закріплення знань, проте можливе їх використання на будь-якому етапі уроку.
Робота з дидактичними матеріалами сприяє формуванню в учнів умінь знаходити в професійній ситуації суттєві ознаки математичного поняття, використовувати вивчені раніше поняття в нових умовах.
Для того , щоб говорити про свідомі і глибокі знання з математики, недостатньо констатувати вміння формулювати означення, теореми, аксіоми, потрібно ще й уміти застосовувати отримані знання до розв’язування задач, у тому числі і до задач з практичним змістом. (ДОДАТОК 1)
Розв’язування цих задач допоможе формувати просторову уяву, обчислювання вміння і навички, графічну культуру, вміння працювати з вимірювальними приладами. Учні удосконалюють уміння і навички в роботі з таблицями, довідковою літературою.
Основне завдання школи - дати підростаючому поколінню глибокі та міцні знання основ наук , сформувати навички та вміння застосовувати їх на практиці. Навчання учнів пошуку відповідей до задач, що виникли в практиці людей різних професій, через створення або добір математичних моделей , вимагає особливої методики, яка поки використовується рідко та непослідовно. Зрозуміло, що з цієї причини реальні задачі прикладного характеру викликають розгубленість навіть у тих учнів, які добре засвоїли матеріал шкільних підручників.
Відомо, що геометрія виникла з потреб практики спочатку у вигляді набору найпростіших правил розв’язування прикладних задач.
Нині в учителя математики є можливість розглянути прикладні задачі на заняттях , де увага учнів фіксується на особливостях прикладних задач, що суттєво відрізняє їх від суто математичних задач.
У суто математичній задачі для знаходження шуканої величини (наприклад, об’єму певного тіла) в умові вже дано всі необхідні числові значення (тобто числові характеристики об’єкта, що нас цікавлять), і при тому їх саме стільки, скільки потрібно для одержання відповіді. На відміну від цього у прикладній задачі зазвичай дано лише сам об’єкт. Учневі, що розв’язує задачу, належить самому вибрати ті параметри, ті характеристики об’єкта, які він знайде шляхом вимірювання або обчислення і які забезпечать йому можливість обчислити шукану величину. Вибір тих чи інших параметрів для безпосереднього вимірювання залежить від фізичних особливостей об’єкта, від вимірювальних інструментів, від обсягу знань учнів, від конкретних умов. Тому реальна прикладна задача переважно відрізняється деякою невизначеністю:числові дані для її розв’язування не пропонуються, їх учневі потрібно отримати самому.
Відомо, що під час розв’язування прикладної задачі ми часто навіть не здогадуємося, що користуємося її математичною моделлю, де замість реальних об’єктів маємо справу із математичною ідеалізацією. У шкільній практиці вибір такої моделі тривіальний (підлога класної кімнати – площина, прямокутник, стакан – циліндр, відро – зрізаний конус, класна кімната - паралелепіпед ). Але особливо цікаві задачі, для розв’язування яких доводиться вибирати нетривіальну модель. У такій ситуації найбільш повчальним, цінним для учні є його власний пошук, його пропозиції щодо вибору моделі з наступним вибором тих параметрів, які він вважає найбільш доцільним знайти безпосереднім вимірюванням. Якщо вибір моделі і параметрів для вимірювання повідомлені учням заздалегідь, то основна дидактична цінність задачі загублена. Вибір тієї чи іншої моделі диктується певними факторами: простотою потрібних вимірювань, необхідною точністю.
Розглянемо, як приклад задачу, яку можна застосувати на уроці в групі підготовки за спеціальністю штукатур, лицювальник – плиточник .
Задача. Для бетонування підлоги у їдальні училища привезли пісок. Цю купу піску необхідно перенести у приміщення. Скільки відер необхідно для такого перенесення?

Щоб розв’язати задачу, необхідно оцінити об’єм піску в купі. Як це зробити?
За формою купа піску помітно відрізняється від відомих нам просторових фігур; віддалено вона нагадує круговий конус. Для об’єму конуса маємо формулу:
![]() .
.
Проте навіть допустивши, купа піску має форму конуса, складно безпосередньо виміряти значення R і H. Можемо вважати, що основою конуса – моделі служить круг, коло якого має таку саму довжину, як периметр основи купи. Цю довжину можемо виміряти безпосередньо шнуром: якщо вона дорівнює С, то ![]() . Висоту Н теж важко виміряти безпосередньо, але легко за допомогою шнура знайти довжину «перекидки» : l=AS+SB.
. Висоту Н теж важко виміряти безпосередньо, але легко за допомогою шнура знайти довжину «перекидки» : l=AS+SB.
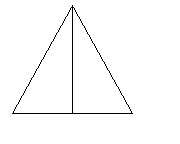 S
S
H
A B
R O
Тоді 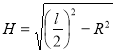 .
.
Розв’язуючи прикладні задачі, потрібно звертати увагу на те, що відсутні в умові числові значення , необхідні для розв’язування параметрів об’єкта, що розглядається, інколи повністю визначаються його якісними особливостями.
В умові даної задачі йдеться про конкретний сипучий матеріал. При вільному насипанні сипучого матеріалу у вигляді купи, близької за формою до конуса, крутизна не може бути довільною; для кожного сипучого матеріалу кут природного відкосу (кут нахилу твірної до площини основи конуса) свій; для піску він наближено становить 450. Ці дані дозволяють спростити розв’язування задачі та знайти об’єм купи піску за допомогою лише одного виміру, а саме – довжини «перекидки» l.
Справді, 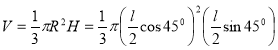 .
.
Чим точніша математична модель, тим відповідь до прикладної задачі буде точнішою; неправильні формули не можна застосовувати для отримання правильного розв’язку задачі. Тому для розв’язування прикладних задач нерідко пропонують використовувати формули, які начебто суперечать формулам, відомим з геометрії. Однак не потрібно виправляти ці формули на відомі правильні. Усе визначається вибором моделі, а вибір моделі диктується певними вимогами. Найважливіші з них – це простота необхідних вимірювань і алгоритму розв’язування при задовільній точності.
Створення математичних моделей до практичних задач помітно полегшується , коли учень, який розв’язує задачу, мав або має можливість побачити даний об’єкт. Тому важливо, щоб навіть у навчальних умовах звернення до джерела інформації не звелося лише до діалогу з учителем і при тому у класній кімнаті. Необхідно використовувати життєвий досвід учнів, досвід їх трудової діяльності , а також практикувати постановку задачі безпосередньо на реальних об’єктах.
Розв’язування прикладних задач корисне з багатьох точок зору. По-перше, учні оволодівають схемою розв’язування прикладних задач. По-друге, у них розвивається прикладна математична культура, формуються необхідні навички застосування математичних знань і способів дії під час розв’язування прикладних задач. По-третє, учні ознайомлюються з роллю математики в практичній діяльності (у широкому розумінні – роль теорії у практиці).
Добре дібрані задачі прикладного характеру сприяють пробудженню інтересу учнів до курсу математики, створюють впевненість в її корисності і практичній значимості. Тим самим ці заняття закріплять уявлення учнів про виникнення і розвиток геометрії в результаті практичної та виробничої діяльності людей, а також розумінні ролі критерію практики при оцінюванні значимості та цінності теоретичних знань.
Професійна спрямованість уроків стереометрії полягає в тому, щоб учні могли на практиці використовувати знання , набуті на уроках. Теоретичні положення стереометрії знайшли широке використання в будівництві. На уроках стереометрії можна застосовувати різноманітні методи, які допомагають закріпити набуті знання на практиці.
Це може бути:
- бесіда з учнями;
- евристичний метод;
- метод питань та відповідей;
- лекції;
- тестові завдання;
- підготовка доповіді учнями;
- робота на комп’ютері;
- використання інтерактивних методів навчання;
- групова робота;
- робота в парах;
- метод само - та взаємоперевірки;
- робота на індивідуальних картках;
- застосування карток із системою само оцінювання.
Важлива роль стереометрії в загальноосвітньому фундаменті професійної підготовки сучасного молодого робітника особливо яскраво окреслюється в теперішній час. Робітник повинен уміти підставити числові дані у формулу, зрозуміти та проаналізувати отриману відповідь, виготовити креслення, підрахувати кількість потрібного матеріалу.
Завдання, не пов’язані із практикою, забуваються. Знання з математики повинні бути пов’язані з винахідливістю, практикою, умінням застосовувати у роботі.
При відповідному математичному підході викладач має великі можливості зробити процес вивчення теорії активним, цілеспрямованим, ефективним. Ці методичні рекомендації та задачі розраховані на зв'язок теорії із практикою.
Задача 1. Визначити площу керамічної плитки й кількість плитки, необхідної для обкладання підлоги, що має форму шестикутника , розміром 2,3х3,1м, якщо плитка має форму правильного шестикутника зі стороною: а=0,25м.
Розв’язання
1.Для обчислення площі плитки використаємо формулу для обчислення площі правильного шестикутника:
![]()
- Визначити площу підлоги:
2,3х3,1=7,13(м2).
3. Визначити необхідну кількість плитки:
![]()
Відповідь. Для обкладання підлоги необхідно не менше 99 плиток.
У практиці будівництва довжину лінії на площині вимірюють за допомогою стрічки, дроту, рулетки. Часто виміри необхідно виконувати на нахиленій площині, при цьому визначають величину проекції цієї лінії на горизонтальній поверхні. Для цього в одержане значення вводять поправку на нахил лінії ∆lк м: ![]() ,
,
де h – перевищення одного кінця стрічки щодо другого;
l – довжина вимірювальної лінії.
Задача 2. Довжина вимірювальної нахиленої лінії -100м, перевищення однієї точки над другою -3,5м. Обчисліть поправку ∆lк та горизонтальне значення лінії.
Розв’язання
1. ![]()
2. L0=100-0,06=99,94(м).
(Так, як горизонтальна проекція завжди менша похилої, поправку віднімають).
Доведемо , що з точки зору математики ця формула може бути використана .
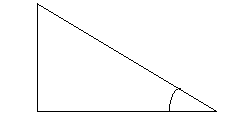
L
β
L0
За теоремою Піфагора знаходимо :
![]() .
.
Піднесемо до квадрату ліву і праву частини виразу:
![]() .
.
∆l дуже мале порівняно з L0, тому вираз у дужках можна прийняти 2 L0.
Отже, ![]() і
і ![]() .
.
Розв’язок подібних задач вчить майбутніх будівельників не сприймати все в готовому вигляді, а побачити в кожній формулі глибокий зміст, уміти вивести її, виховується творчий підхід до роботи.
Відомо, що з давніх-давен геометричні положення були основою для розвитку архітектури і будівництва. Володіння основами геометрії дозволяє майбутньому будівельнику успішно та раціонально розв’язати практичні проблеми. Геометричні задачі з будівельною тематикою допоможуть викладачам у формуванні в учнів науково обґрунтованих професійних навичок.
Так при вивченні многогранних кутів корисно розв’язати декілька задач на знаходження елементів покрівель будинків.
Задача 3. Завіси даху утворюють прямокутник ABCD. AB=12м; BC=30м; кут нахилу скатів – 300. Довести , що нахили скатів рівні. Знайти площу поверхні покрівлі.
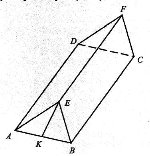
Розв’язання
1.Скати даху представляють собою рівні прямокутники BCFE і ADFE .
2. Прямокутник ABCD розташований горизонтально.
3. Площина трикутника ABE і CDF перпендикулярні до площини ABCD.
4. Так як скати даху – прямокутники, то EF паралельна AD. Отже, за ознакою паралельності прямої і площини EF паралельна площині ABCD.
5. Скат BCFE утворює двогранний кут, ребро якого – ВС. Побудуємо лінійний кут двогранного кута. Проведемо EK перпендикулярно АВ, оскільки ∆ АВЕ перпендикулярний ABCD, то ЕК перпендикулярно ABCD. Похила ВЕ перпендикулярна ВС, отже, її проекція ВК перпендикулярна ВС. Отже, кут АВЕ=β – лінійний кут двогранного кута, який утворений скатом BCFE і площиною ABCD.
Аналогічно можна довести, що кут ЕАВ – лінійний кут двогранного кута, який утворений скатом AEDF і площиною ABCD.
6. Розглянемо трикутник АВЕ, він рівнобедрений, отже, кут ЕАВ дорівнює куту ВАЕ, тому вони - рівні і є двогранними кутами. Отже, скати даху нахилені до горизонталі однаково.
7. Sпокр. =2.ВЕ.ВС;
![]()
Sпокр. =2.30.6,93 = 415,81 (м2).
Відповідь. Sпокр. = 415,81 (м2).
Задача 7. Наскільки збільшиться вартість штукатурки в даному приміщенні , якщо товщину штукатурного намету збільшити на 2мм; на 5мм.
Примітка . Вартість одного мм штукатурного намету на 1м2 – 5грн.
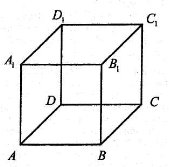
Розв’язання
1.Визначити площу, яку необхідно відштукатурити:
S=2х(АВ+ВС)хАА1=2х(2,5+4)х2,75=35,75 (м2).
2. Якщо шар штукатурки збільшити на 2мм і відомо, що вартість штукатурки на 1м2 становить 5грн., то одержимо:
С1= 35,75.2.5=357,5 (грн..).
3. Якщо шар штукатурки збільшити на 5мм , то одержимо:
С1= 35,75.5.5=893,75 (грн..).
Відповідь. При збільшенні шару штукатурки на 2мм вартість штукатурних робіт у даному приміщенні збільшиться на 357,5 (грн..). При збільшенні шару штукатурки на 5мм вартість штукатурних робіт збільшиться на 893,75 (грн..).
В дидактичних матеріалах, призначених для формування теоретичних знань, можна запропонувати учням вибрати потрібну для розв’язання формулу; вимагати від учнів співставити дані вказаної теореми і співвідношення між цими даними з конкретними об’єктами з виробничої практики; зробити певні висновки для об’єктів, які розглядають.
Як приклад, можна навести задачі , які розв’язуються на уроках із учнями , що навчаються за спеціальністю штукатур, лицювальник – плиточник, маляр. З допомогою дидактичного матеріалу можна організувати актуалізацію знань, опорних для засвоєння нових професійно значимих понять і теорем. Повторення проходить в професійній ситуації.
1. Чи можна використовувати формулу площі бічної поверхні призми для знаходження витрат: а) розчину, який іде на побілку стелі і стін; б) плиток, які потрібні для покриття цоколя житлового приміщення. Відповідь обґрунтувати.
2. В яких випадках на виробничій практиці доводиться мати справу з кутами між двома площинами, які перетинаються? Наведіть приклади вимірювання таких кутів при виконанні виробничих операцій.
3. Наведіть приклади перекриття приміщень і споруд, які мають : а) призматичну; б) циліндричну; в) сферичну поверхню.
4. Виявилося, що маркування на технічні дані змішувачів розчину СО-80 і С-368 стерлася. Які виміри необхідно виконати, щоб розрахувати об’єм розчину в бункері кожного змішувача? Яка з формул в цьому випадку знадобиться: ![]() ?
?
5. Є два твердження: а) пряма, яка проходить через дві різні точки площини, лежить у цій площині; б) через дві прямі, які перетинаються , можна провести одну площину. Співставте умови тверджень із початковими діями операції перевірки якості обробленої поверхні штукатурами при роботі із шпателем і правилом; столярами при роботі з контрольною лінійкою. Зробіть висновок відносно правильності використаного методу перевірки. Поясніть свою відповідь відповідними операціями з інструментами і пристроями.
6. При шпаклюванні шпатель тримають під різними кутами до поверхні, яка вирівнюється. Покажіть за допомогою шпателя кути, які утворюються. Якої величини вони допускаються, як залежить величина кута від товщини шару шпаклівки? Як називаються такі кути в геометрії?
7. Пригадайте послідовність операцій при розмітці панелей на сходових клітках. Як обґрунтувати правильність розмітки панелей, застосовуючи теорему про перпендикулярність двох прямих площини? Зробіть відповідний малюнок, який підтвердить ваші висновки. Яка теорема планіметрії тут використовується?
З навчальною метою дидактичні матеріали пропонуються слабшим учням для індивідуальної роботи. Бажано до тексту задачі додати повний або частковий план розв’язування. Такі завдання можуть бути направлені на перевірку знань фактичного матеріалу програми, наприклад, формул, означень виду поверхонь.
8. Потрібно поштукатурити дві колони однакової висоти, але з різним поперечним перерізом : круглим і квадратним. Зовнішній діаметр круглого перерізу і сторона зовнішнього квадрату дорівнюють 30см. На яку колону витратиться більше штукатурки і у скільки разів?
9. При недотриманні норми товщини штукатурки допускається перевитрата сировини і грошей. Підрахуйте, на скільки збільшиться вартість штукатурних робіт при обробці стін приміщення (довжина-4м, ширина-5м, висота-3м), якщо товщину штукатурки збільшити на 2мм? на 5мм? (Примітка: вартість 1мм штукатурки на 1м2 становить ______)
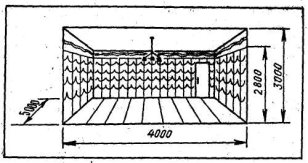
10. Скільки годин потрібно маляру для покраски панелі висотою 2м в приміщені (дані попередньої задачі) щіткою і валиком , якщо норма часу для покраски 100м2 поверхні щіткою -6,4год, валиком -3,4год.?
Розкриття практичного і прикладного значення матеріалу, що вивчають, - один з ефективних прийомів прикладного спрямування курсу математики. Цьому сприяють задачі-запитання, розв’язування яких супроводять розглядом навколишніх об’єктів. Натуральні навколишні об’єкти – важливий вид наочності. З їхньою допомогою можна продемонструвати мимобіжні, паралельні та перпендикулярні прямі у просторі, лінійні кути між площинами, розміщення площин у просторі.
Прикладне спрямування можна здійснювати і за допомогою розв’язування окремих традиційних задач, що є у підручниках. Для цього умови таких задач наближують до практичних потреб.
Для учнів, які навчаються за спеціальністю кравці , можна пропонувати задачі такого типу:
Задача . У швейному цеху є 38м тканини. На пошиття піжами треба 4м тканини, а на халат – 3м. Скільки можна пошити піжам і халатів з наявної у цеху тканини?
Принагідно треба намагатися впливати на уяву, фантазію учнів, діяти через захоплення, здивування. Не варто втрачати можливість розв’язувати на уроках математики прикладні задачі.
Часто в учнів виникає думка, що прикладні задачі потрібні в житті і їх слід навчитися розв’язувати , а всі інші –ні. Щоб не створювалися такі помилкові уявлення, бажано використовувати будь-яку можливість, щоб показати та переконати учнів: майже кожна абстрактна задача може бути математичною моделлю деякої прикладної задачі. Тому доцільно розкривати прикладне значення матеріалу, що вивчається ; наближувати зміст традиційної задачі до життєвих ситуацій; пропонувати учням самостійно складати і розв’язувати задачі ; практикувати розв’язування задач з теоретичним навантаженням суміжних дисциплін.
2.2. Прикладна спрямованість матеріалу, пов’язаного із вивченням многогранників
Викладання стереометрії побудоване таким чином, що учням дуже важко зрозуміти, у яких сферах реального життя вони зможуть використати отримані знання. Вона стала абстрактним предметом, в учнів немає мотивації до її вивчення. Повернути інтерес до цієї важливої шкільної дисципліни можна виключно за рахунок демонстрації практичного застосування геометрії, її понять та методів у реальній практичній діяльності. Викладання цього предмету необхідне у зв’язку з потребами у кваліфікованих кадрах у різноманітних царинах людської діяльності.
Серед прикладних задач доцільно виділити задачі без числових даних або задачі-запитання. У таких задачах чітко сформульовано запитання, але умова їх не повна, даних часто не вистачає або і зовсім немає (Як знайти діаметр дерева? Як виміряти кут нахилу даху? Як знайти товщину аркуша вашого підручника з математики? Як знайти об’єм сірника?) Такі питання часто виникають у практичній діяльності людей і корисно знати, які дані потрібні для їх розв’язування , як їх визначити. До задач без числових даних можна віднести і задачі на побудову, і геометричні задачі на екстремуми (Як з металевої пластинки, що має форму трикутника, вирізати квадрат найбільшої площі?). Під час розв’язування таких задач учні проявляють кмітливість, у них розвиваються практичні вміння набувати знання.
Враховуючи сучасні суспільні умови, завдання реалізації прикладної спрямованості курсу математики є актуальним. Його розв’язування залежить від двох чинників : педагогічної майстерності вчителя і вмінь учнів застосовувати метод математичного моделювання для розв’язування спочатку навчальних, а потім і реальних проблем.
Проблема реалізації прикладної спрямованості стереометрії, завжди займала і займає належне місце при викладанні певної теми.
Можна подати змістовні та корисні рекомендації щодо прикладної спрямованості стереометрії.
Це : - систематичне пов’язування навколишнього світу зі стереометрією: проведення невеликих історичних екскурсів, показ реальних об’єктів, які є основою для створення математичних моделей – стереометричних тіл, розв’язування прикладних задач; бесіди про важливість геометричних знань, умінь та навичок людям багатьох професій;
- введення у навчання методу математичного моделювання в явному вигляді;
- проведення практичних та вимірювальних робіт.
Першою фазою реалізації прикладної спрямованості стереометрії є фаза постановки цілей навчання, які повинні бути сформульовані як особистісно значимі для учнів. Друга фаза – це орієнтація змісту курсу стереометрії.
Розпочати слід із повідомлення цілей вивчення теми «Призма». Вони повинні бути визначені на базі чинної програми, але сформульовані через призму інтересів та потреб учнів відповідних спеціальностей.
Розпочати вивчення даної теми варто із розповіді вчителя учням про призму, історичний аспект вивчення теми.
«Ми вже з вами говорили про геометричні тіла, зокрема, по многогранники. Тому ви маєте уявлення про опуклі та не опуклі многогранники, про їх грані, ребра, вершини, поверхню. А якої форми тіла найбільш поширені у навколишньому середовищі? Назвіть їх. (кришка стола, сірникова коробка, балки, форма будинків та кімнат, цеглина). Як відомо у стереометрії нас цікавить форма тіл та їх розміри. У названих предметів схожа форма. (основи –паралельні та рівні, бічні грані-прямокутники або квадрати) Поверхня всіх тіл складається зі скінченої кількості многокутників, причому, дві грані-рівні п-кутники, а решта п граней – паралелограми. Такі тіла називаються призмами. У перекладі з грецької слово призма .
Вивчення далеких періодів людської культури, сліди якої навчилася розпізнавати археологія, підводить до переконання , що спочатку споруди були неправильної форми: в них позначилася звичка людини до використання природних укриттів – печер. Чому ж багато будинків сьогодні – це споруди, які мають форму прямокутних паралелепіпедів? Прямокутна система побудови архітектурної форми була обумовлена статичною основою споруд, будівельними матеріалами, головним чином деревом. Людина створила собі світ прямокутних речей, видобуваючи із природи те, що може послугувати її потребам, - це результат діяльності людського розуму.
Наприклад , Велика Китайська стіна – фортечна стіна у Північному Китаї, була споруджена в 4-3 ст. до н.е. для захисту від нападу кочових племен. Її довжина 5тис.км, висота – (в середньому) 8м, а ширина -5м.
Існує багато інструментів призматичної форми. Масштабна лінійка-основна її частина являє собою чотирикутну призму трапецеподібного перерізу. Напилок – слюсарний інструмент, який служить для обпилювання металічних виробів. Він являє собою чотирикутну призму із ромбовидним перерізом. Гайка має форму правильної шестикутної призми. Гайки використовуються у з’єднанні із болтом, як кріпильна деталь для з’єднання двох (або більше) деталей машин або предметів. Болт є круглим стержнем, на одному кінці якого є головка у вигляді правильної шестикутної призми. В частинах, які скріпляються , висвердлюється круглий отвір, де вставляється болт, що загвинчується гайкою.
У спорті теж не обходяться без знарядь у формі призми. Спортсмени стрибають у висоту через дерев’яну планку трикутного перерізу 3х3 см або через дюралеву трубку діаметром 23-26мм , в обидва кінці якої вставляють дерев’яні буші трикутного або квадратного перерізу.
У фехтуванні використовуються три види холодної зброї. Рапіра –колюча зброя; має легкий еластичний клинок прямокутного перерізу довжиною 90см. Маса рапіри-500г. Шпага –колюча зброя із жорстким тригранним клинком довжиною 90см. Маса шпаги -770г. Шабля – зброя; має клинок довжиною 105см фігурного перерізу, з подовжніми пазами на бічній частині.
Для гри в настільний теніс виготовляють стіл висотою 0,76м від підлоги. Для кришки беруть фанеру або дошки товщиною 30мм. Розмір кришки –2,74м х 1,525м.. М’яч використовують із целулоїду або пластика масою 2,5г.
Для природи , яка оточує людину, прямокутна форма жодною мірою не є характерна, правильна форма окремих кристалічних утворень ніяк не спростовує цього твердження. Кристали різних речовин відрізняються один від одного формами. Кубики кристалів кам’яної солі не сплутаєш зі стовпчиками берилу або табличками мідного купоросу; форму шестигранних призм має кварц.
В природі дуже мало об’єктів призматичної форми. Цікавою є інформація про місцевість в Африці, яка називається Низький Велд. Характерна для цього ландшафту –численні невеликі пагорби , які тут відомі як «копі». Це груди, практично кубічних валунів, ніби поскладених один на одного рукою людини. За схожістю зі старовинними баштами їх називають «замками » копі. Характерна прямокутна форма валунів пояснюється тим, що з’єднувальний матеріал вивітрюється швидше, ніж тверда серцевина кожного блоку.
Рослин призматичної форми не існує. Проте – у басейні Нілу (краї неосяжних боліт) росте папірус, з якого в давнину в Єгипті виготовляли папір. Папірус має тригранні стебла висотою до 4,5м.
І звичайно , стільники у вуликах мають шестигранну форму. Будовою стільників дуже давно цікавилися не лише математики. Займалися нею філософ-фізик Аристотель(І У ст. до н.е.) , природознавець Пліній Старший (І ст.. н.е.), фізик Реомюр (ХУІІІ ст..), математики: Папп(ІІІ ст..), Ян Брожек (ХУІІ ст..), Кеніг, Маклорен, Люйллер (ХУІІІ ст..), Лаланд, Браутгхам (ХІХст.) . Бджоли своєму житлу надавали таку форму, щоб за мінімальних витрат матеріалу(воску) та витрат часу побудувати найбільш просторе приміщення і максимально раціонально використати невеликий простір вулика. Вже Піфагор помітив, що існує лише три види правильних многогранників, за допомогою яких можна без порожніх місць покрити всю площину навколо будь-якої точки: рівносторонній трикутник, квадрат і правильний шестикутник. Лише одна із цих фігур може бути основою комірки (із мінімальним периметром і максимальною площею поверхні). Таку властивість має правильний шестикутник.
Після опрацювання відповідного стереометричного матеріалу , потрібно застосувати отримані знання для розв’язування прикладних задач. Саме потреби практики, життя привели до створення та вивчення поняття призми.
Для прикладу подані зразки задач, які можна розв’язувати з учнями на уроках стереометрії , незалежно від їх професійної підготовки. Усі задачі із професійним змістом готувалися за допомогою викладачів спецдисциплін , майстрів виробничого навчання відповідно до професій.
І. Задачі на обчислення площі поверхні призми.
1. Коробка для упаковування подарунка має форму низької призми із ромбом в основі. Найбільша відстань між протилежними кутами кришки 24см, а найменша-10см. Висота коробки 4см. Скільки потрібно квадратних сантиметрів кольорового паперу, щоб обклеїти коробку (крім дна)?
2 . Для обклеювання тільки з боку іншої, але такої ж за формою коробки, яка має висоту 5см і відстань між двома протилежними кутами 10см, використали 260см2 паперу. Скільки необхідно паперу для обклеювання кришки?
3. За умовою задачі у (1) визначте площу перегородки із картону, яка проходить усередині коробки між найближчими її кутами і між більш віддаленими кутами, а також периметр кришки.
4. Результати обчислень попереднього випадку візьміть за умову та визначте кількість паперу, потрібного для обгортання коробки, якщо для цього витрачено паперу на 30% більше, ніж для обклеювання всієї коробки.
5. Складіть ще задачу (візьміть із основної задачі дані на вибір).
(Відповідь. 1) 328см2; 2) 120см2; 3) 96см2; 40см2.)
6. Для виготовлення квадратного ящика висотою 80см без кришки і дна використали дошку довжиною 6,4м і шириною 4,3м. Скільки таких дощок піде на дно та кришку? На відходи додати половину дошки. Як сформулювати цю задачу, використовуючи лише геометричні терміни? (Відповідь .≈6 дощок)
7. Для відправлення товарів виготовлено 80 кубічних ящиків довжиною по 106см. Скільки дощок пішло на ящики, якщо на 1м2 ящика потрібно приблизно 1 дошку? Дошка має довжину 496см, а ширину-222см. (Відповідь. 535 дощок)
8. Прямокутна кімната довжиною 5,6м, шириною 3м і висотою 2,5м обклеєна шпалерами. В кімнаті є вікно шириною 2,3м і висотою 1,3м та 2 дверей шириною по 1,1м і висотою 2,1м. Скільки потрібно мати рулонів шпалер, якщо довжина кожного рулону 10м і ширина 53см? (Відповідь . ≈7)
9. Для оклеювання шпалерами стін кімнати використано 93,5м2 шпалер. Вікна та двері займають 15,1м2. Бордюр, яким обклеєні шпалери вздовж всіх стін, має довжину 25,5м. Скільки буде коштувати фарбування підлоги цієї кімнати, якщо за фарбування олійною фарбою кожного квадратного метра беруть 3 гривні і якщо висота кімнати менша від її ширини на 1,42м? (Відповідь.121 гривень.)
10. Потрібно зацементувати підвал глибиною 2м, шириною 2,5м і довжиною 4м. Скільки потрібно використати для цього пудів цементу, якщо на кожний квадратний метр дна йде 2 пуди, а на квадратний метр стіни – 0,8 пуда цементу? (Підвал має форму прямокутного паралелепіпеда). Міра. 1 тонна = 61 пуд. (Відповідь. 668 кг.)
11. Двосхилий дах має форму 3-гранної призми; дах простягається уздовж будинку на 21м, ушир – 8,5м, а висота даху (підйом) – 3,2м. Скільки м2 займає поверхня даху? (Відповідь. 227м2.)
12. Прямокутника садиба, довжиною 153м, шириною 115м, обнесена парканом, який має висоту 213см. За скільки часу 4 малярі зможуть пофарбувати з двох стін паркан з воротами та хвірткою, якщо 1 маляр фарбує за день 40,9м2 паркану? (Відповідь.14 днів.)
13.Стайня довжиною 17м, шириною 11м, висотою від землі до даху – 496см, зроблена із цегли. В стайні знаходяться: 2 дверей висотою по 284см, шириною 195см; 6 вікон шириною по 709см, висотою по 355см. Скільки пішло цегли на стіни стайні, якщо на 1м2 стіни потрібно198 штук цегли? (Відповідь. 52500штук.)
ІІ. Задачі на обчислення об’єму призми.
1. Цукор-рафінад виготовляють у вигляді шматочків форми прямокутного паралелепіпеда розміром 24х24х10мм. Скільки шматочків цукру повинно міститись у пачці масою 0,5 кг? Питома вага цукру 1,2 г/см2. (Відповідь. ≈70 штук.)
2. Коробка для цукерок має форму прямої призми, основою якої є ромб. Бічна поверхня коробки 900см2 , діагональ дна 40см. Коло, що обкреслює картинку на кришці і дотикається сторін кришки, має довжину 75,36см. Скільки кілограм цукерок може вмістити коробка, якщо 1кг цукерок займає приблизно 2400см2? (Відповідь. 2,2 кг)
3. 260см2 мила має масу 410г. Яка маса шматка мила, що має форму прямокутного паралелепіпеда, якщо : а) площа однієї грані шматка складає 96см2 , площа розрізу через діагоналі обох основ 120см2 , а діагональ основи (через яку проведено розріз) більша від сторони основи, через яку проходить дана в задачі бічна грань, на 2см; б) бічна поверхня шматка більша площі однієї з бічних граней на 910см2 ; довжина бічного ребра 20см, периметр основи 62см. (Відповідь. а) 922г; б) 7656г)
4. Об’єм книги 786м3 , довжина-27см, товщина-2,2см. Яку ширину має книга? (Відповідь.13см )
5. Яку масу мають 650 цеглин, якщо довжина кожної цеглини 24см, ширина-12см, товщина-5см? ρ=1800кг/м3. (Відповідь. ≈1685кг)
6. Скільки цеглин потрібно для кладки 18 стовпів висотою 4м з перерізом у вигляді квадрата зі стороною 7дм? Розмір цеглини1дмх1,5дмх3х дм .Додати 5% на злам. (Відповідь. 13272)
7. Коридор має 21м довжини та 2,1м ширини й уміщує в собі 161м3 повітря. Знайти висоту коридору. (Відповідь. 3,7м)
8. Для здоров’я учнів необхідно, щоб у класі на кожного учня припадало не менш ніж 6м3 повітря. Клас довжиною 10м, шириною 6м, висотою3,5м. Скільки учнів може знаходитися в ньому без шкоди для здоров’я? (Відповідь. 35)
9. Глибина класу (відстань від вікон до внутрішньої стіни) не повинна перевищувати 7,1м, щоб віддалені парти були достатньо освітлені. Довжина класу не повинна перевищувати 9,9м, щоб учні, які сидять за задніми партами чітко розрізняли написане на дошці. На кожного учня повинно припадати не менш ніж 6м3 повітря. Беручи до уваги, що повітря вище за 3,6м не бере участь в переміщенні повітряних шарів, обчислити, яка найбільша кількість учнів може одночасно навчатися у цьому класі? (Відповідь. 42)
10. Кубатура однієї кімнати будівлі дорівнює 120м3 . Обчислити кубатуру іншої кімнати, якщо її ширина в 1,5 рази більша від ширини першої , а довжина в 3 рази менша. (Відповідь. 60м3)
11. Для фундаменту кам’яної стіни, що оточує будинок (довжина будинку 383м, ширина-250м) потрібно викопати рів шириною 0,53м і глибиною 36см. За скільки годин зможуть виконати цю роботу 7 землекопів, якщо 3 землекопи за 13 годин викопають 19м3 землі, і якщо три хвіртки мають по 4,3 довжини? (Відповідь. 63 години)
12. Підлога в прямокутному залі викладена мармуровими плитками. Кожна плита має форму правильної 8-кутної призми зі стороною основи 6,4см і товщиною2,5см. Яку площу займає займає підлога , якщо маса всіх плит 89690кг? (Відповідь. 140м2)
13. Стіни та дно прямокутного басейну викладені плитами. Довжина басейну 11м, ширина -6,4м, а глибина -4,3м. Яка маса всіх плит, якщо на 1м2 поверхні басейну йде 313кг плит? Товщина плити 13см, а маса 1м3 плити 2352кг. (Відповідь. 469222кг)
14. Конопляне масло , яке перелили в посудину кубічної форми глибиною 7,6см, має масу 411г. Яку масу має 16,4см3 масла ? (Відповідь. 15г)
У ході розв’язування прикладних задач учні повинні коментувати , як саму умову , так і відповідь, висловлювати свої пропозиції щодо вдосконалення або створення іншої умови задачі. Тому потрібно організувати роботу по складанню прикладних задач. Можна подати їм для цього певний матеріал.
Чимало солі розчинено у Світовому океані. Спеціалісти підрахували, що, якби раптом випарувалася вода всіх морів і океанів , солі, накопиченої в осаді , було б достатньо для побудови стіни товщиною 1м і висотою 280м, яка оперезала б нашу планету по екватору.
Площа Світового океану 361млн км2, середня його глибина 3,799км. Радянський океанолог М.Львович оцінює океан в 1370млн км3.
Американські економісти підрахували, що вартість усіх речовин , розчинених у 1км2 морської води, за розцінками другої половини ХХст., дорівнює 1млрд доларів.
Спеціалісти вважають, що в середньому урагані за добу випадає близько 20млрд т води. В рекордних випадках під час тропічного циклону на кожну одиницю площі випадає за добу стовп води висотою 2500мм, це в 4-5разів більше за річну суму опадів для Москви.
Один з механізмів прикладної спрямованості курсу стереометрії можна показати на прикладі вивчення теми «Піраміда».
Вивчення теми можна розбити на кілька етапів.
- Емпірична основа (Піраміди в історії. Єгипетські піраміди. Таємниці пірамід. Доцільність та естетика пірамідальних форм. Піраміди в техніці, побуті, будівництві.)
- Створення математичної моделі. (Поняття про піраміду. Види пірамід. Зрізана піраміда. Елементи піраміди.)
- Дослідження математичної моделі. (Зображення піраміди на площині. Перерізи. Площа поверхні. Об’єм .)
- Застосування математичної моделі. (Розв’язування прикладних задач.)
Доцільно запропонувати історичні задачі, що виникли в різних частинах світу.
Задача 1. Піраміда Хеопса спочатку мала висоту 147м і займала площу 34300м2. Скільки тонн речовини потрібно було для облицювання споруди, якщо на 1м2 використовували її 160кг?
Задача 2. Піраміда Хеопса мала висоту 147м2 , сторона її квадратної основи -230м. Внутрішні ходи і приміщення займають 30% її об’єму . Визначити масу каменю, який пішов на її спорудження. (Маса 1м3 каменю дорівнює 2,5т. )
Задача 3. Форма для сирної паски (правильна 4-кутна зрізана піраміда) складається з 4 бічних дощечок, з’єднаних гачками, дна і дощечки, на яку ставлять гніт. Визначити висоту форми, якщо площа бічних дощечок становить 1700см2, площа усіх дощечок -2376см2 , а висота бічної дощечки – 25см.
Задача 4. Відома піраміда Хеопса в Єгипті має форму правильної чотирикутної піраміди. її висота 138,75 м, а площа основи 5,29 га. Знайдіть кут нахилу її бічного ребра до площини основи.

Пропоную задачі, у яких розглянуто використання геометричних методів у технічних сферах для учнів підготовки за спеціальністю кухар, кондитер, і також будівельних професій. (Додаток 2, Додаток 3)
Як зразок подаю також задачі професійної спрямованості, які відображають виробничий процес гірничої промисловості.
- Поперечний перетин польового штреку має форму рівнобічної трапеції, у якої основи рівні 3,4м і 2,6м, а кут при нижній основі рівний 800. Скільки тонн породи буде в трьох погонних метрах вироблення, якщо об’ємна вага породи рівна 2,2т/м3?
-
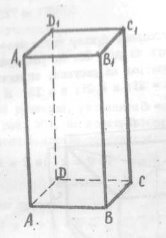 Довжина лави 220м, посування лінії забою лави за місяць 202,8м. Потужність пласта складає 2,09м. Скільки тонн вугілля складає місячний видобуток вугілля для цієї лави, якщо об’ємна вага вугілля 1,3т/м3?
Довжина лави 220м, посування лінії забою лави за місяць 202,8м. Потужність пласта складає 2,09м. Скільки тонн вугілля складає місячний видобуток вугілля для цієї лави, якщо об’ємна вага вугілля 1,3т/м3?
- Копер скіпового ствола шахти має форму прямокутного
паралелепіпеда, у якого довжина рівна 5м, ширина 4м,
висота рівна 39м. Скільки листків жерсті буде потрібно для
обшивки корпусу копра, якщо розміри листка жерсті 0,7х1,4, а на
шви витрачається 1% необхідної кількості жерсті.
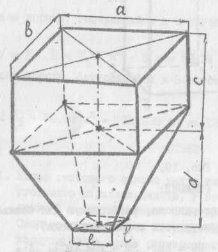
- Приймальний вугільний бункер шахти має форму,
зображену на малюнку. За розмірами, вказаними на
малюнку , визначити об’єм бункера:
а=21, в=21, с=15,d=10, l=3.
Під час проведення позаурочного заходу «Піраміда – творіння людського генія», крім висвітлення історичного матеріалу і його демонстрації, пропоную учням наступні матеріали.
1. Задачі - цікавинки .
1. Яку відстань треба пройти людині, щоб обійти Велику піраміду?
(знайти периметр основи)
Наше училище займає площу 966кв.м. Скільки таких училищ можна було б
розмістити на площі основи Великої піраміди?
Висота одноповерхового будинку Зм. Із скількох поверховим будинком можна
порівняти висоту цієї піраміди?
Кожен , хто приходить подивитися на піраміду, мріє піднятися на її вершину.
Зрозуміло, що турист підніматиметься гранню піраміди і вибере найкоротший
шлях до її вершини. Де ж цей шлях і яка його довжина?
2. Прикладні задачі
Бічна поверхня піраміди дорівнює 260м2, в її основі - прямокутник зі сторонами 5
та 8м. Обчислити повну поверхню піраміди.
Повна поверхня піраміди дорівнює 240м2 , площа її бічної поверхні -180м' .
Знайти площу основи.
Накреслити розгортку чотирикутної піраміди, в основі якої прямокутник, а всі
бічні ребра однакової довжини. Уявіть, що з цієї розгортки ви зробили піраміду.
Обчисліть її повну поверхню.
Піраміду будували шар за шаром. Поступово вона зростала. Щоб побудувати
наступний шар, кам'яні блоки затягували на гору похилими насипами. Кожен
кам'яний блок важив близько 2,5тонн - як великий джип. На будівництво піраміди
Хеопса пішло 2 300 000 блоків. Хто швидше підрахує їхню загальну вагу?
На гранях піраміди написані фрагменти слів, кожне з яких пов'язане з темою
«Піраміда». Хто зможе якнайшвидше скласти ці слова?
Написані частини слів : гр пет об ниця фара ань вер он шипа гр сги об.(Вершина, грань, гробниця, Єгипет, об'єм, фараон)
Підрахуйте якнайшвидше кількість ребер шестикутної піраміди.
Висота піраміди Хеопса дорівнює 147м, її основа квадратної форми завдовжки
230м. Обчисліть об'єм піраміди.
В Єгипті, крім пірамід, є ще Асуанська гребля, збудована в 1971 році за
допомогою радянських спеціалістів. її висота -11м, довжина-3,8км. На п
будівництво витрачено таку кількість каменю, піску, глини та бетону, що з цього
матеріалу можна було б побудувати 17 пірамід Хеопса. - Яка вага цього
матеріалу ?(використати результат задачі 4)
3. Віршовану задачу – загадку:
Пише цар і не вгаває:
« Чарівну я шапку маю.
Що туди не покладеш -
Втроє більш назад візьмеш.
Шапка ця чотирикутна,
А боки її - трикутні.
ЗО сантиметрів має
Висоту, і не спадає.
Ще додам (може , й не влад):
Є основою квадрат,
Сторона (лічи вже ти) –
Половина висоти.
А який об'єм займає,
Я бажання знати маю.
Шапку цю носив мій дід,
Тож обчисліть все як слід»
То який вигляд має шапка царя?
Я сподіваюся, що цей матеріал допоможе вчителям математики зробити крок назустріч учням і показати їм використання геометрії у реальній життєвій практиці.
Основне завдання запропонованих задач - показати основні концепції та специфічність практичних методик, а не складність арифметичних розрахунків.
2.3. Прикладна направленість матеріалу, пов’язаного із вивченням тіл обертання.
Тіла циліндричної форми дуже поширені. Стовбури дерев мають приблизно циліндричну форму. Їх використовують для будівництва жител, мостів та інших споруд. Ця форма поширена і в архітектурі. Наприклад, колони циліндричної форми прикрашали величні споруди стародавньої Греції. Циліндричну форму мають резервуари для нафти, циліндричні труби, катки для укачування асфальту, цистерни для молока, корпуси водонапірних башт, ринви, рулони паперу, шпалери, валики для побілки і покраски і т.д.
Циліндричну форму має основна частина космічної ракети, яка містить двигуни і пальне.
У Франції навіть споруджено багатоповерховий будинок циліндричної форми. До речі, дають про нього позитивні відгуки.
У швейній промисловості багато предметів і деталей швейних машин мають циліндричну форму:
- вали (головний, розподільний, човниковий, вал переміщення );
- голкотримач;
- шестерні;
- складова частина регулятора натягу верхньої нитки;
- центрові пальці;
- барабани механізму човника і т.д.
Котушки швейних ниток мають циліндричну форму. Футляр для сантиметрової стрічки – порожнистий циліндр.
А скільки побутових предметів, з якими ми зустрічаємося у повсякденному житті, мають форму циліндра. Засоби побутової хімії містяться у циліндричних упаковках. Флакони і тюбики для косметичних засобів часто виготовляють циліндричної форми.Якщо розглянути власну кухню, то предметів даної форми там безліч.
Дослідженнями циліндричних поверхонь і їх властивостей займалися досить давно.
Спосіб обчислення бічної поверхні циліндра знайшов ще Архімед.
Те, що всі точки кола однаково віддалені від центра, безпосередньо застосовується на практиці. Наприклад, в автомашині, завдяки коловій формі ободу колеса, вісь, на якій воно обертається при русі автомашини, весь час залишається на одному рівні від поверхні, по якій переміщується автомашина. Внаслідок цього забезпечується горизонтальне переміщення пасажирів або вантажу.
Цікаво, що людина з зав’язаними очима не може іти по прямій лінії. Вона обов’язково зійде з прямого шляху на коловий. Є багато прикладів, коли люди, які заблудилися, поверталися у вихідне місце.
Те саме спостерігається і у тварин. Собака з зав’язаними очима плаває по колу. Зацькований звір, що втратить від страху свідомість, рятуючись від переслідування, біжить по колу. У цьому не має нічого дивного. Адже, щоб зберегти прямолінійний напрям, не контролюючи його очима, тіло повинно бути точно симетричним, а це в живій природі абсолютно не можливо. Отже, рух по колу відбувається в описаних випадках через асиметричну розвиненість правої і лівої руки, сторін тіла людини і тварини. А коли людина або тварина рухається з відкритими очима, то останні корегують їх рух.
При введенні поняття „тіло обертання” потрібно сказати учням, що більшість деталей, які виточують на токарних станках із металу і дерева – тіла обертання. І посуд, виготовлений на гончарних кругах, і скляні банки, пляшки, графини, стакани, пробірки, і різноманітні котушки , барабани, вали, шайби, заклепки, лінзи, патрони, снаряди, спортивні диски, м’ячі, обручі – це все матеріальні тіла, що мають форму тіл обертання.
Циліндричні резервуари і цистерни, хокейні шайби, графітні стержні, електроди для електрозварювання, круглі олівці – всі вони мають форму прямого кругового циліндра. І шахтний стовбур, бурова неглибока свердловина, отвір , просвердлений у дошці перпендикулярно до її поверхні, циліндр двигуна внутрішньо згоряння або поршневого насосу – також циліндри.
Ще більше зустрічається матеріальних циліндрів у комбінації з іншими тілами: призмами, кулями пірамідами, циліндрами. Наприклад, цегла з отворами, залізобетонна панель для перекриття, труба, просвердлена по осі куля.
При переході до вивчення конусів варто вказати, що природно насипані на горизонтальній поверхні купи піску, зерна , вугілля, породи мають форму конусів. При цьому кожному сипучому матеріалу відповідає певний кут природного укосу (кут нахилу твірної до площини основи конуса). Так, наприклад, пісок має кут укосу - 250, глина – 300, гравій – 330, вугілля – 420.
Інші приклади матеріальних конусів: нижня частина заглиблення , зроблена свердлом в металі, верхні частини багатьох нафтосховищ. Форму зрізаного конуса мають відра, тазики, ролики багатьох підшипників.
Приклади матеріальних куль – кульки підшипників, кулі в дробилках, цукерки драже, м’ячі, більярдні кулі.
Приклади прикладних задач.
- Скільки мідної проводки діаметром 5мм можна прокатати із зливка об’ємом 0,5м3?
- Скільки у зв’язці електродів для електрозварювання, якщо їх загальна маса 10кг, а кожен електрод – кусок сталевої проводки довжиною 45см і діаметром 6мм? Густина сталі 7600кг/м3.
- Знайти об’єм шахтного стовбура діаметром 8м, якщо його глибина 800м.
- Залізобетонна панель має розміри 600х120х22см. По усій її довжині – 6 циліндричних отворів, діаметри яких 14см. Знайти масу панелі, якщо густина матеріалу 2,5т/м3.
Зрозуміло , що обчислення тут будуть наближені.
Корисно звернути увагу на термінологію. Висоту матеріального тіла не завжди називають висотою. Говорять про довжину проводу, стержня, про глибину ямки, свердловини, про товщину прокладки.
Особливу увагу слід приділити задачам про труби. Є безліч труб – водогінні, опалювальні, газові, каналізаційні, водовідвідні, вентиляційні. На задачах про труби добре ілюструвати і закріплювати формули об’єму і площі поверхні циліндра.
- Зовнішній і внутрішній діаметри кілька для колодязя відповідно – 1,3м і 1,1м, а висота 0,9м. Скільки кубометрів бетону потрібно для виготовлення 8 таких кілець?
- а) Знайти масу десятиметрової труби діаметром 1420мм, зробленої із сталевого листа товщиною 22мм. Густина сталі 7600кг/м3.
б) Скільки тонн таких сталевих труб потрібно, щоб прокласти газопровід Уренгой – Ужгород, довжина якого4451км?
в) Знайти загальний об’єм (внутрішній) газопроводу.
г) Знайти площу поверхні десятиметрової труби діаметром 1420мм.
д) Скільки квадратних метрів ізоляційної стрічки потрібно, щоб двічі покрити нею труби газопроводу?
На місцевому матеріалі можна скласти безліч задач такого типу (розміри труб – стандартні).
Бажано розв’язувати задачі і про рулони (поліхлорвінілова плівка для обмотки газопроводів, папір і кіно- чи фотоплівки). Нерідко виникає потреба дізнатися про площу матеріалу, змотаного у рулон. Це робиться за допомогою формули об’єму циліндра.
- Скільки квадратних метрів паперу у рулоні, висота і радіуси якого відповідно 85см, 45см і 2см, якщо товщина паперу 01мм?
При вивченні конуса слід розглядати задачі про терикони.
- Скільки тонн породи в териконі висотою 90м, якщо відомо, що кут природного укосу породи 460, а її густина 2т/м3?
Немало прикладних задач можна розв’язати при вивченні кулі, сфери і їх частин.
Для учнів ,які готуються стати кухарями можна запропонувати таку прикладну задачу .
Задача. Що вигідніше : купити кавун радіусом 30см або три кавуни радіусом 10см ?
Розв'язання .
Об'єм кавуна обчислимо за формулою об'єму кулі:
![]()
Знайдемо об'єм великого кавуна із радіусом R=30см;
![]() .
.
Обчислимо об'єм трьох малих кавунів : R=10см,
![]()
Як бачимо, вигідніше купити кавун радіусом 30 см.
Для гірників можуть бути запропоновані задачі такого змісту:
1.Поперечний перетин шахтного ствола – круг діаметром 3,5м. Шахта пройдена на глибину 67,6м. визначити об’єм вийнятого грунту.
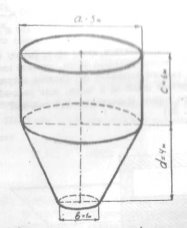 2. Визначити кількість повітря, що подається вентилятором місцевого провітрювання в глухий забій гірничої виробки за 1хв., якщо швидкість руху повітря по трубопроводу складає 8м/сек, а діаметр трубопроводу складає 0,6м.
2. Визначити кількість повітря, що подається вентилятором місцевого провітрювання в глухий забій гірничої виробки за 1хв., якщо швидкість руху повітря по трубопроводу складає 8м/сек, а діаметр трубопроводу складає 0,6м.
3. За розмірами, даними на малюнку (а=5м, в=1м, с=6м,
D=4м) визначити об’єм вугленавантажувального бункера, що
має форму комбінації циліндра і зрізаного конуса.
4. Визначити , скільки залізничних платформ вантажопідйомністю 25т потрібно для перевезення конусоподібної купи вугілля, заввишки 7,5м. об’ємна вага вугілля рівна 1,3 т/м3.
 5. Знайти продуктивність двоциліндрової
5. Знайти продуктивність двоциліндрової
компресорної установки за 1хв, якщо діаметр циліндра
низького тиску рівний 570мм, діаметр циліндра високого
тиску рівний 340мм, хід штока рівний 300мм і число
ходу штока рівно 330.
Для майбутніх кравців певні завдання вказують на роль математики у майбутній професії.
Приклади задач.
1.У швацьку майстерню надали заказ на виготовлення чохлів до диванних валиків, довжина валика 80см, а діаметр 24см. Скільки квадратних метрів меблевої тканини потрібно для пошиву 10 чохлів, якщо на залишки від крою відходить 15% тканини?
2.Знайти висоту та радіус циліндричної частини капелюха, який має найбільшу площу бокової поверхні, якщо периметр осьового перерізу дорівнює 2р.
3.Дві диванні подушки валики одягають в чохли. Довжина одного валика в 2 рази більше другого, але радіус цього основи вдвічі менше другого. На який чохол пішло більше тканини?
4.Скільки квадратних метрів тканини необхідно для пошиву намету діаметром основи 4м і висотою 3,5м?
5.Потрібний чохол на подушку у вигляді півкулі об’ємом V. Визначте діаметр.
6.Розкрій елегантного модного пончо являє собою в основі 2 великих півкола. Скільки кв.м тканини потрібно у чистому вигляді на пончо довжиною 0,7м? припуск на шви – 5см.
Можна підібрати окремі питання для методу фронтального бліц-опитування.:
- Назвіть деталі у швейному обладнанні , які мають форму тіл обертання.
- Яку форму має прямий рукав у зшитому вигляді?
- Які розрахунки потрібно зробити для крою сумки-бочечки?
Можна поставити перед учнями проблемні ситуації для вибору оптимальних шляхів їх вирішення.
- У швацькому виробництві застосовуються обкантувальні стрічки, скісні бейки, найрізноманітніші види тасьми, а також рулони тканин флизеліну, синтепону, ватину. Всі вони мають якісну характеристику на довжину, ширину та інше. Після того як ці матеріали побували у роботі може виникнути необхідність знати залишок метражу в котушці чи рулоні. Замір вручну шляхом перемотки неможливий. Проблема : як бути?
Досить урізноманітнює роботу викладача по застосуванню задач із професійним спрямуванням використання на уроках ПРЕЗЕНТАЦІЙ .
Один із зразків такого використання хочу продемонструвати на розробці уроку у групі кравців на тему «Циліндр».
Тема уроку. Циліндр.
Дидактична мета: розглянути означення циліндра і пов’язаних із ним понять , окремі види перерізів. Виробити в учнів навики і вміння виділяти вивчені тіла циліндричної форми у виробництві.
Розвиваюча мета: формувати просторову уяву, логічне мислення.
Виховна мета: виховувати в учнів інтерес до математики, до досліджень.
Обладнання: моделі тіл обертання, моделі циліндрів із перерізами, плакат, опорні конспекти, розгортка циліндра, шаблони еліпсів, креслярські інструменти, деталі швейних машин, підручники, презентація «Циліндр у моїй професії».
Хід уроку
І. Організаційний момент.
ІІ. Мотивація навчання.
Вчитель. На попередньому уроці ми закінчили вивчення одного із розділів стереометрії «Многогранники». І сьогодні ми приступаємо до вивчення нової теми, яка носить назву «Тіла обертання».
Сама тема уроку говорить, що ми будемо мати справу із фігурами чи тілами, які утворюються внаслідок обертання чогось навколо чогось.
Світ, що нас оточує складається із безлічі круглих тіл. Це – коло, круг (відомі вам здавна), циліндр, конус, куля, сфера, і інш. (показати усі виставлені у кабінеті моделі).
Якщо заглибитися у історію математики, то найкраще було б здійснити екскурс у Стародавню Грецію. Адже там, завдяки землемірним роботам, потреб архітектури і астрономії вводилися нові геометричні поняття., серед яких – тіло обертання.
Близько 300років до н.е. визначний математики Евклід в ХІ книзі своїх Начал вперше вводить поняття «циліндр». Він вказує, що циліндр - це фігура, яка утворюється при обертанні прямокутника навколо однієї з його сторін як осі(показати на моделі).
Циліндр (греч. kэlindros, вал, каток) — геометричне тіло, обмеженою циліндровою поверхнею (званою бічною поверхнею циліндра) і не більше ніж двома поверхнями (підставами циліндра); причому якщо підстав два, то одне отримане з іншого паралельним перенесенням уздовж створюючої бічної поверхні циліндра; і підстава перетинає кожну створюючу бічній поверхні рівно один раз.
Слово циліндр часто зустрічається в техніці.
Предмети, що мають більш менш точну форму циліндра, а також і такі, у яких є деталі циліндрової форми, зустрічаються повсюдно: у побуті, в будівництві, в техніці – і грають важливу роль. Осі автомобілів і вагонів, циліндри і поршні двигунів і так далі – всі вони мають головні частини у вигляді кругових циліндрів. Сталеві труби є прямі циліндри з тонким круговим кільцем в підставі.
Під циліндром розуміють зазвичай круглі предмети, але якщо у вигляді циліндри в нашому загальному сенсі, то можна привести безліч інших прикладів. Рейки, різні види прокату, бетонні жолоби і інші вироби мають різноманітні форми циліндрів (хоч і не круглих). У практиці їх характеризують формою перпендикулярного перетину. Колони, якщо вони не звужуються догори, стовпи балки в будівельних конструкціях мають форму циліндрів, зокрема, призм, прямих і похилих.
Запишіть, будь-ласка, тему уроку «Циліндр».
ІІІ. Сприймання і усвідомлення поняття циліндра і пов’язаних з ним понять.
(Показати, як обертається прямокутник; пояснити що утворюється, дати сучасне означення).
Означення. Циліндром ( точніше, круговим циліндром) називається тіло, Що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів. (записати його).
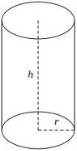
Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, - твірними циліндра (показати на плакаті і на моделях).
Згадаємо властивості паралельного перенесення.
Учениця. Оскільки паралельне перенесення є рух, то основи циліндра рівні.
Через те що при паралельному перенесенні площина переходить у паралельну площину (або в себе), то основи циліндра лежать у паралельних площинах.
Оскільки при паралельному перенесенні точки зміщуються вздовж паралельних прямих або прямих, що збігаються на одну й ту саму відстань, то твірні циліндра паралельні і рівні.
Поверхня циліндра складається з основ і бічної поверхні. Бічна поверхня – з твірних.
(показати на плакаті і на моделях).
Вчитель. Знаючи властивості паралельного перенесення і те, що паралельною проекцією кола є еліпс, побудуємо циліндр (пояснити побудову і виконати з учнями).
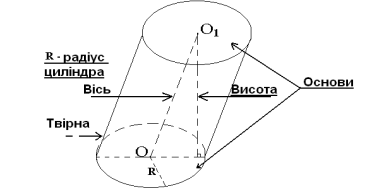 Циліндр, як і будь-яке тіло, має поверхню. З чого ж складається циліндр? Ще раз гляньте на модель фігури і плакат.
Циліндр, як і будь-яке тіло, має поверхню. З чого ж складається циліндр? Ще раз гляньте на модель фігури і плакат.
Учні. Поверхня циліндра складається з двох кругів, які є основами і бічної поверхні , яка утворена твірними.
Якщо твірні циліндра перпендикулярні до площини основи, то циліндр називається прямим. Циліндр, як тіло обертання має радіус і вісь.
Радіусом циліндра називається радіус його основи.
Висота - відстань між площинами його основ.
Вісь - пряма, що проходить через центри основ.(провести демонстрацію на моделях).
На практиці дуже часто доводиться мати справу із перерізами фігур. Розглянемо, які перерізи може мати циліндр.
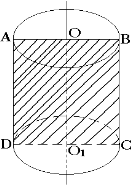
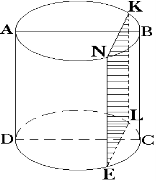
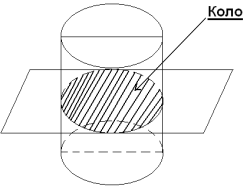
Переріз циліндра площиною, яка проходить через вісь називається осьовим перерізом. Це прямокутник.
Переріз циліндра площиною , паралельною основам є круг.
Якщо побудувати переріз циліндра площиною, розміщеною під певним кутом до осі, то отримаємо еліпс.
Перерізи дуже с часто використовують при розв’язування задач.
Якщо поверхню циліндра розрізати по твірній і колах основ і розгорнути, то ми отримаємо фігуру, яка називається розгорткою циліндра.
З чого вона складається ?
Учениця. Це два круги і прямокутник (бічна поверхня), сторони якого рівні висоті циліндра і довжині кола основи.
Вчитель. У повсякденному житті поряд із звичайним циліндром розглядають і порожнистий циліндр або циліндричну трубу.
4. Систематизація знань.
Вчитель. А зараз узагальнимо все, що сьогодні ви почули на уроці за таким планом (фронтальне опитування):
- означення циліндра;
- основи;
- твірна;
- поверхня;
- радіус;
- висота;
-перерізи;
- розгортка.
(Учні відповідають)
Вчитель. З давніх давен усе, що приймалося теоретично, вимагало перевірки на практиці.
На виробничому навчанні ви працюєте на швейних машинах різних марок, які складаються із багатьох деталей, серед яких є і такі, що мають циліндричну форму.
При перегляді презентації «Циліндр у моїй професії» (Додаток 4), знайдіть потрібні елементи і прокоментуйте їх .
(Учні знаходять необхідні елементи, називають їх і коментують їх призначення).
5.Підсумок уроку
- оцінити знання учнів,
- домашнє завдання (на відкидній дошці) : підготувати виступи про практичне використання циліндра, виконати рисунки деталей циліндричної форми, скласти кросворд «Циліндр у моїй професії».
По темі «Об’єми тіл обертання» зроблено добірку задач для слюсарів з ремонту автомобілів.
Задача 1. Знайти об'єм пальної суміші в циліндрі автомобіля КамАЗ, знаючи, що внутрішній діаметр циліндра 120 мм, а робочий хід поршня 120 мм.
Задача 2. Ролик радіально-опорного підшипника має форму зрізаного конуса з діаметрами основ 5 мм і 6 мм та висотою 7 мм. Знайти об'єм матеріалу, з якого виготовлено ролик.
Задача 3. Редукційний клапан двигуна автомобіля ГАЗ 53 має форму кулі діаметром 8 мм. Знайти об'єм клапана.
Задача 4. На будівництво необхідно завести труби для монтажу мережі водопостачання. У зв'язку із цим треба виконати наступні розрахунки .
1) Знайти об'єм труби діаметром 60 мм і довжиною 3 м, якщо товщина металу, з якого виготовлена труба, становить 5 мм.
2) Скільки таких труб можна навантажити на автомобілі ЗИЛ-130 і КамАЗ-5320, якщо вантажопідйомність ЗИЛ-130 - 6000 кг, а КамАЗ-5320 - 8000 кг (густина металу
р = 7,8 г/см3 = 7800 г/см3).
3) Кузов автомобіля ЗИЛ-130 має внутрішні розміри 3752 мм х 2326 мм х 575 мм, а розміри кузова КамАЗ-5320 становлять 5200 мм х 2320 мм х 500 мм. Який автомобіль і у скільки разів продуктивніше працюватиме під час перевезення вантажу, якщо час навантаження, транспортування та розвантаження, буде однаковим?
4) Обчислити витрати палива та його вартість під час перевезення 250 труб вантажними
автомобілями ЗИЛ-130 і КамАЗ-5320 на відстань 30 км (ціна 1 л бензину А-80 - 4,80 грн,
дизельного пального - 5,05 грн).
5) Зварник виконав завдання з монтажу системи водопостачання та виконав 20 стикових швів труб діаметром 60 мм. Який заробіток отримав робітник, якщо плата за виконання 1 м стикового шва становить 42,1 грн?
Задача 5. Ролик підшипника кочення має форму циліндра, висота якого 20 мм, діаметр основи 10 мм. Знайти об'єм матеріалу, з якого виготовлено ролик.
Задача 6. Відро має форму циліндра, діаметр якого 26см, а висота 35 см. Скільки поміститься у відрі, якщо його наповнити доверху?
Задача 7. Скільки тонн бензину можна зберігати в цистерні циліндричної форми, якщо її діаметр 4 м, а довжина 3 м? (Густина бензину 700 кг/м .)
Задача 8. Купа піску має форму конуса, довжина кола основи якого дорівнює 25,12 м, а твірна -5 м. Скільки автомобілів вантажопідйомністю 3 т потрібно для її перевезення, якщо маса 1 м становить 2 т?
Задача 9. Маса кульки дворядного сферичного підшипника дорівнює 3 г. Який її діаметр (р = 7,8 г/см3)?
Задача 10. Яким повинен бути радіус основи циліндричного бачка висотою 6 м, щоб у нього помістити 50 т бензину (густина бензину 0,7 т/м3)?
Отже, вивчення стереометричного матеріалу в ПТНЗ має носити практичний характер, базуватися переважно на дослідах, інтуїції, експерименті; тим самим буде сформовано необхідний запас просторових уявлень на науково-теоретичному рівні для подальшого використання у майбутній професії.
Стереометричний матеріал має вивчатися на наочно-оперативному рівні . Це дасть змогу одночасно з формуванням знань, навичок і вмінь формувати просторові уявлення, розвивати просторову уяву. Вивчення елементів стереометрії має здійснюватися систематично, з дотриманням принципів навчання. Метою та засобом навчання учнів елементам стереометрії мають бути різнопланові задачі: на розпізнавання геометричних фігур і їх виготовлення; на зображення, вимірювання та обчислення величин. Значна їх кількість має мати професійну спрямованість. У ході розв'язування задач в учнів мають формуватися просторові уявлення та уява, практичні навички та вміння. Вивчення стереометрії має проводитися диференційовано. Основними критеріями диференціації мають бути рівень вимог до засвоєння учнями навчального матеріалу та рівень допомоги їх з боку вчителя з урахуванням індивідуальних відмінностей.
ВИСНОВКИ
Сучасний кваліфікований робітник повинен добре уявляти положення свого місця, ділянки роботи в діяльності свого підприємства. Щоб відповідати вимогам, кваліфікований робітник повинен постійно узагальнювати та поповнювати свої загальні технічні та спеціальні знання, професійні навички та вміння, творчо використовувати знання, одержані в училищі.
Отже, якщо сучасний вчитель математики у процесі навчання шкільного курсу акцентує увагу учнів на зв’язок математики з життям, то він викликає у дітей інтерес до навчання, добитися формування таких важливих рис характеру як послідовність у роботі, наполегливість, акуратність, увагу, критичне ставлення до своєї роботи й роботи своїх товаришів, кмітливість, чесність, колективізм, любов до праці .
Також розв’язування прикладних задач сприяє ознайомленню учнів з роботою підприємств і галузей народного господарства, що є умовою орієнтації інтересу учнів до певних професій. Використання прикладних задач дозволяє вдало створювати проблемні ситуації на уроці. Такі задачі стимулюють учнів до здобуття нових знань. Збагачують учнів теоретичними і практичними знаннями з технічних та інших дисциплін.
Прикладна спрямованість шкільного курсу стереометрії - одна із цілей математичної освіти і основа, на якій опанування учнями математичних знань, вмінь та навичок їх використовувати, відбувається значно ефективніше. Забезпечення прикладної спрямованості сприяє формуванню стійких мотивів до навчання взагалі й до вивчення математики зокрема. Способи та засоби її реалізації , які вже були розроблені раніше, у нових суспільних умовах та вимогах сьогодення до рівня, якості та характеру математичної освіти набувають актуальності за умови модернізації, уточнення та розширення.
Прикладна спрямованість шкільного курсу стереометрії – це орієнтація цілей, змісту та засобів навчання стереометрії в напрямку набуття учнями в процесі математичного моделювання знань, вмінь і навичок, які використовуватимуться ними у різних сферах життя.
Вона містить потенціал формування продуктивного мислення, гуманізації навчання (за рахунок диференціації навчання і посилення мотивації), гуманітаризації навчання (залучення учня до творчої діяльності, наприклад, складання прикладних задач; озброєння учнів методом наукового пізнання – методом математичного моделювання; здійснення міжпредметних зв'язків, поповнення інтелектуального багажу старшокласника суспільно значимими знаннями про оточуючий світ).
Прикладна орієнтація цілей навчання забезпечує презентацію стереометрії (її окремих розділів, тем) як потрібного та важливого предмета, дозволяє викликати і підтримувати інтерес та зацікавленість у його вивченні.
Дієвими засобами прикладної спрямованості є комплексне використання методу математичного моделювання як способу вивчення курсу стереометрії і основи для формування вмінь, навичок розв'язувати прикладні задачі; застосування протягом вивчення стереометрії дидактичних матеріалів із прикладною інформацію; систематичне розв'язування та створення учнем власних прикладних задач; унаочнення стереометричних об'єктів за допомогою їх моделювання ; доцільне та систематичне використання сучасних інформаційно-комунікаційних технологій .
Вивчення стереометрії на основі явного введення методу математичного моделювання дає можливість вивчати курс стереометрії як систему математичних моделей, які створені на основі реальних об'єктів шляхом розгляду їх форми та розмірів, що формує вміння геометричного бачення світу та науковий світогляд учнів. Система базується на певній математичній моделі (моделях), етапи вивчення кожної з них співвідносяться з етапами реалізації математичного моделювання. Учневі ПТУ корисно мати зразок того, який зміст, обсяг знань та характер умінь та навичок він може досягти. Це дозволяє йому планувати, корегувати та контролювати свою навчальну діяльність. Посилюється мотивація вивчати абстрактний стереометричний матеріал, розв'язувати абстрактні стереометричні задачі для формування знань та вмінь дослідження математичних моделей. З'являються передумови для того, щоб знання, які отримують учні, набули такі якості, як систематичність, системність.
Робота зі складеною системою прикладних стереометричних задач виступає ефективним засобом активізації пізнавальної діяльності старшокласників. Це відбувається завдяки підвищенню пізнавального інтересу, досягається зосередженням уваги на значенні стереометричних знань у реальному житті.
Пропонована методика реалізації прикладної спрямованості узгоджується із віковими, психологічними особливостями учнів старшої школи.
Розроблена методика реалізації прикладної спрямованості курсу стереометрії дозволяє врахувати окремі ідеї диференціації навчання: профіль навчальної групи, рівень навченості конкретного учня. Це проявляється на підготовчій та початковій (мотивація навчальної діяльності) стадіях реалізації даної методики; на основній стадії у процесі відбору тематики прикладних задач із створеної системи (технічні задачі, історичні тощо).
Наочне моделювання окремих геометричних тіл є важливим фактором розвитку математичної інтуїції, просторового та креативного мислення, формування інтересу до вивчення стереометрії.
Методика реалізації прикладної спрямованості курсу стереометрії не ставить вимогу використовувати переважно певні методи навчання та організаційні форми, хоча і надає перевагу у формі рекомендацій окремим з них. Ця методика дозволяє легко поєднуватись із пануючою традиційною системою навчання, підкреслюючи існуючі, притаманні їй позитивні риси, нівелюючи недоліки, зокрема, орієнтацію навчальної діяльності на середнього учня, розв'язування лише абстрактних задач тощо. Вона сприяє підвищенню якості математичної підготовки учнів, посилює їх пізнавальну діяльність, допомагає подолати формалізм у навчанні, формувати позитивні мотиви навчальної діяльності та, як наслідок, сприяє досягненню учнями практичної компетентності, яка свідчить про готовність молоді до повсякденного життя, найважливіших видів суспільної діяльності, оволодіння майбутньою професією.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Бевз Г.П. Геометрія в загальноосвітній школі/ Г.П.Бевз//Математика в школах України.-2003.-№1.- с.18.
2. Возняк Г., Маланюк М. Взаємозв'язок теорії з практикою в процесі вивчення математики. — К.: Рад. шк., 1989.
3. Волосюк О.В., Онопченко С.В. Педагогічні аспекти прикладної спрямованості шкільного курсу математики.//Вісник ЛНУ імені Тараса Шевченка. – 2010. – № 17 (204). – С.36-40.
4. Возна М. Спроби формування цілісної картини навколишнього світу в процесі навчання математики// Математика в школах України.-2005.-№30.
5. Державний стандарт базової і повної середньої освіти //Математика в школі.-2004.-№2.
6. Збірник тестових завдань з математики для абітурієнтів / В.І.Беспальчук, А.В.Прус, І.А.Сверчевська та ін.; Під. ред. В.В.Михайленка. – Житомир: ЖДТУ, 2005. – 196с.
7. Коваль В.В.Прикладна спрямованість шкільного курсу математики//Теорія та методика навчання математики, фізики, інформатики:Збірник наукових праць: В 3-х томах.-Кривий Ріг:Видавничий відділ КДПУ, 2001.-Т.1: Теорія та методика навчання математики.-с.142-148.
8. Кушнір Г.А. Драма геометрії//Математика в школах України.-2004.-№8
9. Лук’янова С.М. Роль прикладної спрямованості в навчанні математики учнів 5-6 класів. // Didactics of mathematics: Problems and Investigation. – Issue#28. – 2007. – С.222-227.
10. Панішко Ф. В. Три половини. Математична наука // Математика. — № 7 (211).-2003.
11. Порджерс А. «Саймон Флегг і диявол» // Квант. — 1972. - № 8.
12. Прус А.В. Вибрані питання прикладної спрямованості шкільного курсу стереометрії // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. - Донецьк: Фірма ТЕАН, 2004. – Вип.22. - С.126-131.
13. Прус А.В., Швець В.О. Дискурсивні висновки щодо прикладної спрямованості шкільного курсу стереометрії на основі генезису вказаного поняття // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. – Донецьк: Фірма ТЕАН, 2003. – Вип.20. - С. 126-135.
14. Прус А.В. Евристичне навчання та прикладна спрямованість шкільного курсу стереометрії // Эвристическое обучение математике: Тезисы докладов научно-методической конференции (15-17 ноября 2005г.). - Донецк: Изд-во ДонНУ, 2005. – С. 98-99.
15. Прус А. Піраміда в контексті прикладної спрямованості шкільного курсу стереометрії // Математика в школі. – 2005. – №2. - С. 11-15.
16. Прус А.В. Планування у контексті прикладної спрямованості шкільного курсу стереометрії // Підготовка вчителя у контексті Європейського освітнього простору: Збірник наукових праць. – Київ - Житомир: Вид-во ЖДУ імені Івана Франка, 2005. - С. 88-96.
17. Прус А.В. Про засіб прикладної спрямованості шкільного курсу стереометрії // Науковий часопис НПУ імені М.П. Драгоманова. Серія №2. Комп'ютерно-орієнтовані системи навчання: Зб. наукових праць. – К.: НПУ імені М.П. Драгоманова, 2006. - №4(11). – С. 176-181.
18. Прус А.В. Про засоби здійснення прикладної спрямованості шкільного курсу стереометрії // Вісник Житомирського державного університету імені Івана Франка. – Житомир: Вид-во ЖДУ імені Івана Франка, 2005.–– Вип. 20. - С. 100-103.
19. Прус А.В. Про прикладні задачі шкільного курсу стереометрії // Матеріали Всеукраїнської науково-методичної конференції "Проблеми математичної освіти" (ПМО - 2005), м. Черкаси, - Черкаси: Вид. від ЧНУ ім. Б.Хмельницького, 2005. – С. 126-129.
20. Прус А. Про прикладну спрямованість матеріалу, пов'язаного із вивченням призми // Математика в школах України. – 2005. – №13(97). - С. 1-8.
21. Прус А.В. Про прикладну спрямованість шкільного курсу стереометрії // Вісник Житомирського державного університету імені Івана Франка. – Житомир: Вид-во ЖДУ імені Івана Франка, 2003.–– Вип.13. - С. 45-47.
22. Прус А. Про циліндр у контексті прикладної спрямованості // Математика в школі. – 2005.-– №5. – С. 15-20.
23 Прус А.В. Тема "Куля" в контексті прикладної спрямованості шкільного курсу стереометрії // Дидактика математики: проблеми і дослідження: Міжнародний збірник наукових робіт. - Донецьк: Фірма ТЕАН, 2003. – Вип.21. - С. 85-91.
24. Прус А.В. Чинники прикладної спрямованості шкільного курсу стереометрії // Науковий часопис НПУ імені М.П. Драгоманова. Серія №3. Фізика і математика у вищій і середній школі: Зб. наукових праць – К.: НПУ імені М.П. Драгоманова, 2004. - №1. – С. 41-45.
25. Слобода І.В.Математичне моделювання в процесі розв’язування текстових задач// Теорія та методика навчання математики, фізики, інформатики:Збірник наукових праць: В 3-х томах.-Кривий Ріг:Видавничий відділ КДПУ, 2001.-Т.1: Теорія та методика навчання математики.-с.285-289.
26. Смирнова И., Смирнов В. Профильное обучение геометрии: традиции и современность// Математика .-2004.-№12
27.Соколенко Л.О., Філон Л.Г., Швець В.О. Прикладні задачі природничого характеру в курсі алгебри і початків аналізу:практикум. Навчальний посібник. – Київ:НПУ імені М.П.Драгоманова, 2010. – 128с.
ДОДАТКИ
Додаток 1. Задачі з професійним змістом
- Конусоподібний намет заввишки 4м і діаметром 6м виготовили з поліетиленової плівки. Скільки квадратних метрів плівки пішло на виготовлення намету?
- Яка різниця в об’ємі між глиняною звичайною цеглиною 250х120х65мм і модульною 250х120х88мм (силікатною) ?
- Із жерсті вирізали сектор радіусом 50см і центральним кутом 2160 і загорнули в конус. Знайти об’єм конуса.
- Півкруг згорнули в конічну поверхню. Знайти кут між твірною і висотою конуса.
- Проектується квартира з двох кімнат однакової ширини. Довжину першої хочуть зробити в 1,5 рази більшу від її ширини, а довжину другої кімнати – 7,2м. Знайти ширину кімнат, якщо площа двох кімнат повинна дорівнювати 56,7 м2.
- Розміри бетонного блоку для будівництва стін такі: 2,7х1,4х0,5м. Порожнина блоку складає 20% його об’єму . Скільки потрібно бетону для виготовлення 450 таких блоків?
- За який час буде розпиляна колода завдовжки 9,3м циркулярною пилою, якщо вона робить 400 обертів за хвилину при подачі на один оберт 14,5 мм?
- Визначити діаметр дискової пилки, якщо довжина її кола 628мм?
- стовпчик ртуті в термометрі довжиною 11,7см має масу 3,9г. Знайти площу поперечного перерізу стовпчика. (Густина – 13,6х103кг/м3).
- Щоб засклити одне вікно, потрібно 1, 85м2 скла. Скільки потрібно скла на 78 таких вікон? На обрізку витрачається 8% загальної площі скла.
- З листа скла потрібно вирізати прямокутник, довжина якого в два рази більша за ширину. Якщо ширину прямокутника збільшити на 40мм, то його площа збільшиться на 168см2. Знайти довжину і ширину скла, яке вирізають.
- Скільки дощок завдовжки 4,5 м і завширшки 0,125 м потрібно для виготовлення підлоги в кімнаті розмірами 4,5 х 3,5 м ?
- Соснова колода завдовжки 4м має в обхваті 0,65м. Обчислити її об’єм і масу (густина сосни – 0,31 х 103 кг/м3) .
- Як знайти масу соснової дошки розміром 8х0,3х0,04м, не зважуючи її на вазі?
- 50 м мідного дроту важить 200,14 г. Знайти діаметр дроту. (Густина міді – 8,9х10 3 кг/м 3).
- У кімнаті довжиною 8м і шириною 5м потрібно зробити паркетну підлогу із квадратних дощечок , сторона яких 200мм. Скільки дощечок буде використано на підлогу?
- Залізничний насип у перерізі має форму рівнобічної трапеції з основами 18м та 10м і бічною стороною 5м. Скільки кубічних метрів землі містить 3км насипу?
- Скільки кілограмів покрівельного заліза завтовшки 1мм потрібно на покриття даху, який має форму правильної чотирикутної піраміди зі стороною 4,2 м при довжині схилу 6,5м? На шви та обрізки добавляється 10%. Розміри листа заліза 1400х700мм. Визначити кількість листів, витрачених на покриття даху.
- Соснова колода 18м має діаметри 500мм і 400мм. Знайти об’єм колоди.
- Прокладаючи в гірській місцевості автомагістраль, ширина якої 32м, у горі прорізали тунель заввишки 6м і 23м дороги (переріз гори – трикутник ). Знайти об’єм гірської породи, яку вивезли, прокладаючи дорогу найбільш економним шляхом.
- Кабінет має розміри 6,5х4,8м і висоту 2,7м. Скільки листів дерево плити розміром 1,2х1,5м потрібно, щоб виготовити панелі, висота яких 1,2м? Двері мають ширину 1,5м.
- Знайти площу пофарбованої поверхні і витрати олійної фарби при пофарбуванні дерев’яного ящика розміром по зовнішньому виміру 5,8х2,5х1,7 і по внутрішньому виміру 5,6х2,5х1,5м. Фарбування робиться з двох боків по два рази (якщо без кришки). На 1м2 витрачається 160 г фарби.
- Яка маса золота у золотій каблучці 585 проби масою 4,2г?
- Потрібно обклеїти шпалерами кімнату розміром 5х4х3м. Площа вікон і дверей складає 20% всієї площі стін. Скільки потрібно рулонів шпалер для обклеювання, якщо в рулоні 9м і ширина його 500мм?
- Скільки кубічних метрів розчину витрачено на зовнішню штукатурку стін будинку 65,5х14,5х20,8м? Будинок має 80 вікон розміром 1,6х2,25 і четверо дверей 1,5х2,5м. На один квадратний метр стіни витрачається 0,02м3 розчину. Дати відповідь з точністю до 0,1м.
- З куба виготували найбільшу кулю. Скільки процентів матеріалу сточено? (Ця задача має застосування на підшипниковому заводі.)
- Знайти площу трикутної керамічної плитки зі сторонами 130мм, 140мм, 150мм.
- Підлога кухні розміром 3х2м викладена керамічними плитками розміром 150х150 мм, завтовшки 8мм. Шви між плитками 2мм. Знайти витрати плиток і їх масу.
- Обчислити , скільки розчину необхідно для штукатурки кабінету розміром 6х9,5м при висоті 3м. Кабінет має три вікна розміром 2х1,6м і двері 1,3х2м. На 1м2 витрачається 0,02мл розчину.
- Драбина, довжина якої 20м, приставлена до карнизу будинку під кутом 300 . Знайти висоту будинку від землі до карнизу.
- Відро без кришки має форму зрізаного конуса з діаметрами 30мм і 20мм, а твірна – 0,3м. Скільки потрібно взяти фарби для фарбування з обох боків 300 таких відер, якщо на 1 м2 потрібно 160г фарби?
- Знайти площу пофарбованої поверхні і витрати фарби для фарбування труб діаметром 0,63м, довжина яких 86, 5 погонних метрів, діаметром 0,6 м- 174,75 погонних метрів. Фарбування виконується два рази. Витрати на 1м2 – 130г.
- Потрібно приготувати цементно-вапняний розчин складу 1 : 0,5 : 6. Яку кількість складових компонентів у кубічних метрах необхідно взяти для приготування 1,2м2 розчину?
- Скільки треба рулонів шпалер розміром 10х0,5м, щоб обклеїти кімнату розміром 6х4,8х3,75? Кімната має 4 вікна розміром 1,8х0,75м. На підклейку витрачається 1%площі шпалер.
- Дах водогінної вежі має форму правильної шестикутної піраміди, сторони основи якої 2м, а бічне ребро 4,25м. Скільки потрібно листів заліза розміром 0,7х4м, щоб покрити водонапірну вежу(відходи становлять 10% площі заліза)?
- На кутах листа заліза розміром 142х71см вирізано рівні квадрати із стороною 15см. Із загнутих країв виготовлено відкриту коробку. Знайти її об’єм.
- Свинцевий брусок масою 18кг має форму прямої призми, висота якої 30см. В основі призми лежить рівнобічна трапеція, паралельні сторони якої дорівнюють 3,5 і 11,5см, а бічна сторона 8,5см. Чи цей брусок суцільний ,чи він має пустоту ? (Густина свинцю 11,3х103 кг/м3.)
- Маса мотка мідного дроту діаметром 1,6мм дорівнює 8кг. Визначити довжину цього дроту. (Густина міді – 8,8 х103 кг/м3)
- Прямокутний лист жерсті з розмірами 1,6м і 0,8 м можна зігнути в трубу так, щоб її довжина була або 1,6м або 0,8м. У якому випадку труба охоплюватиме більший об’єм?
- Котел, що має форму півкулі, вміщує 28,6л води. Визначити діаметр котла.
Додаток 2
![]() Стереометрія (задачі професійної спрямованості з професії кухар)
Стереометрія (задачі професійної спрямованості з професії кухар)
Тема. Узагальнення і систематизація знань про властивості фігур за основну школу.
1.Скільки крему треба для оздоблення торта , що має форму рівнобічної трапеції з ребром 20см, основами 50см і 30см , якщо на 1 см2 наносять Зг крему?
2.Тісто розкатали у вигляді прямокутника із сторонами 30см на 50см .
Скільки печива можна вирізати з цього тіста у вигляді круга діаметром Зсм .
Яка площа відходів?
3.Скільки крему треба для оздоблення країв торта площею 314 см2 ?
(на 1см припадає 1г крему)
Тема. Многогранники
1.Скільки потрібно олії для смаження 10 порцій картоплі, якщо на порцію береться 12 брусочків розмірами 1x2x3 кожен? Норма олії на 1см2- 0,8г.
2.На виготовлення 1 порції м'ясного салату норма закладки майонезу
30г. Частину цієї норми треба залишити для оздоблення салату зверху. Скільки
майонезу потрібно залишити для оздоблення 10 порцій салату, якщо він має
форму 4-кутної правильної піраміди висотою Зсм. Із стороною основи 8см і на
1см площі потрібно 0,3г майонезу.
3.Скільки потрібно кулінарного жиру для смаження 10 порцій омлету,
якщо на порцію розмірами 4x5x6 на 1см2 витрачається 0,05г жиру. Омлет має
форму прямокутного паралелепіпеда.
4.Скільки потрібно повидла для прошарування торта, який має форму
прямокутного паралелепіпеда розмірами 12х35х20см, якщо на 1см витрачається
12г повидла?
5.Скільки потрібно джему для оздоблення пирога, який має форму трикутної призми висотою 5см, в основі якої лежить правильний трикутник з стороною 20см, якщо на 1см2 витрачається 2,5г джему?
6.Скільки треба згущеного молока для оздоблення торта, який має форму
прямокутного паралелепіпеда розміром 5x20x10см, якщо на 1см2 витрачається 5г?
7.Скільки потрібно шоколадної помадки для того, щоб оздобити торт, що
має форму прямокутного паралелепіпеда розмірами 25x40x45, якщо на 1см2 витрачається 30г?
8.Цистерна для молока має циліндричну форму. Діаметр основи дорівнює 1,2м. Довжина цистерни - 2м.Скільки літрів молока може вмістити ця цистерна?
![]() 9. Скільки кубічних дециметрів (літрів) води вміщає бак, що має форму циліндра, коли радіус його основи дорівнює 30м, висота - 0,6м?
9. Скільки кубічних дециметрів (літрів) води вміщає бак, що має форму циліндра, коли радіус його основи дорівнює 30м, висота - 0,6м?
Тема. Об'єми геометричних тіл
1.Закладають в циліндричну каструлю небагато рису. Скільки потрібно налити води, щоб вийшла смачна каша ?
2.Склянка має форму циліндра з діаметром основи 12 см і висотою
20см. Скільки порцій чаю можна видати, якщо чай готувати в циліндричній каструлі радіусом 50см і висотою 80 см ?
3.Визначити вагу салату поданого у формі конуса з твірною 10 см та
довжиною кола основи 40 см, якщо 1см3 має вагу 7г.
4.Визначити вагу салату сформованого циліндричною посудиною з
твірною 5 см та довжиною кола основи 30 см, якщо 1см3 має вагу 9г.
5.Два торти циліндричної форми, висотою 12см з діаметром основи
одного з них 20см , а другого — в 2 рази меншого. У скільки разів один торт важчий за другий?
6.50л олії зберігалося у бочці циліндричної форми висотою 80 см.
Протягом тижня олію використовували для приготування їжі і її рівень зменшився на 30 см. У скільки разів зменшився об'єм олії в бочці?
7.Один кухар взяв каструлю радіусом К, висота якої в 2 рази більша
ніж радіус. А другий - каструлю з радіусом 2 К , з висотою у два рази меншою.
Хто з кухарів нагодує більше гостей ?
8.Визначити місткість відра, висотою 40см та діаметрами дна і верх
нього перерізу відповідно 25см і 30см.
Додаток 3
Стереометрія (задачі професійної спрямованості з будівельних професій)
Тема. Узагальнення і систематизація знань про властивості фігур за основну школу.
1. Визначити затрати матеріалів для облицювання поверхні загальною площею 42 м2 плиткою 200x200 мм.
2. Проектується квартира з двох кімнат однакової ширини. Довжину першої
кімнати хочуть зробити в 1,5 рази більшу від її ширини, а довжину другої кімнати
— 7,2 м. Знайти ширину кімнат, якщо площа двох кімнат повинна дорівнювати 56,7м2
3.Щоб засклити одне вікно, потрібно 1, 85м2 скла. Скільки потрібно скла
на 78 таких вікон? На обрізку витрачається 8% загальної площі скла.
4.З листа скла потрібно вирізати прямокутник, довжина якого в два рази
більша за ширину. Якщо ширину прямокутника збільшити на 40мм, то його площа
збільшиться на 168см . Знайти довжину і ширину скла, яке вирізають.
5.Скільки дощок завдовжки 4,5 м і завширшки 0,125 м потрібно для виготовлення підлоги в кімнаті розмірами 4,5 х 3,5 м ?
6.У кімнаті довжиною 8м і шириною 5м потрібно зробити паркетну підлогу із квадратних дощечок , сторона яких 200мм. Скільки дощечок буде використано на підлогу?
7.Знайти площу трикутної керамічної плитки зі сторонами 130мм, 140мм,
150мм.
8.Підлога кухні розміром Зх2м викладена керамічними плитками розміром 150x150мм, завтовшки 8мм. Шви між плитками 2мм. Знайти витрати плиток і
їх масу.
Тема. Вступ до стереометрії.
1 .Як перевірити чи добре відполірована обштукатурена поверхня?
Тема Паралельність прямих і площин. Перпендикулярність прямих і площин
1.Драбина, довжина якої 20м, приставлена до карнизу будинку під кутом
30°. Знайти висоту будинку від землі до карнизу.
2.Через річку з паралельними берегами необхідно побудувати міст, перпендикулярний берегу , щоб дорога від заводу до сировинної бази , які знаходяться
на різних берегах, була найкоротшою.
3.Де будувати їдальню, щоб вона була однаково віддалена від гуртожитку
і заводу ?.
![]()
![]() 4.В яких випадках на виробничій практиці доводиться мати справу з кутами між двома площинами, які перетинаються? Наведіть приклади вимірювання таких кутів при виконанні виробничих операцій.
4.В яких випадках на виробничій практиці доводиться мати справу з кутами між двома площинами, які перетинаються? Наведіть приклади вимірювання таких кутів при виконанні виробничих операцій.
5.Є два твердження: а) пряма, яка проходить через дві різні точки площини,
лежить у цій площині; б) через дві прямі, які перетинаються , можна провести одну
площину. Співставте умови тверджень із початковими діями операції перевірки
якості обробленої поверхні штукатурами при роботі із шпателем і правилом; столярами при роботі з контрольною лінійкою. Зробіть висновок відносно правильності
використаного методу перевірки. Поясніть свою відповідь відповідними операціями
з інструментами і пристроями.
6.Пригадайте послідовність операцій при розмітці панелей на сходових клітках. Як обґрунтувати правильність розмітки панелей, застосовуючи теорему про перпендикулярність двох прямих площини? Зробіть відповідний малюнок, який під
твердить ваші висновки. Яка теорема планіметрії тут використовується?
Тема. Координати і вектори в просторі
1.Вихідна фігура - квадрат К , (плитки на підлогу). Знайти групи рухів, за допомогою яких можна замостити площину.
2. Визначити висоту будівлі, якщо спостерігач, який стоїть на відстані 200м,
тримає на відстані 70см монету діаметром Зсм, що закриває висоту будівлі.
Тема. Многогранники
1 .Скільки рулонів шпалер потрібно для обклеювання кімнати розмірами 2х 5х 2, якщо розмір одного рулону 0,5х 7, а на обрізи досить мати запас, який рівний площі вікон і дверей.
2.Скільки плиток потрібно для лицювання басейну, розміри якого 8x10x2, якщо площа однієї плитки 0,25м2.
3. Кімната має розміри 8м, Зм, 2м. Обчисліть площу стін і стелі, які необхідно
побілити, якщо площа вікон і дверей становить 4м .
4.Кімната має розміри 10м, 5м і 4м. Обчисліть площу стін, які необхідно побілити, якщо площа вікон і дверей становить 5м2.
5. Веранда має розміри 10м, 2м, 4м. Обчисліть площу заскленої частини, якщо вона становить половину площі стін.
6.Скільки фарби потрібно для фарбування призматичного ящика з кришкою, розміри якого 1x1x2, якщо на їм витрачається 100г фарби?
7.Ви працюєте в бригаді плиточників яка виконує облицювання з/б стін приміщення кінотеатру скляною плиткою. Визначити об'єм робіт та витрату плитки розміром 150x150 мм, при ширині шва 2мм, для облицювання стіни (6x3) м.
8.Виконати поліпшену штукатурку цегляних стін приміщення учбового корпусу училища. Визначити об'єм робіт, якщо площа 6x5 м, висота 2,5м, двірний проріз (2,0x0,9) м, . два вікна (175x135) м.
![]()
![]() 9.Басейн має розміри 15м, 8м і 1,8м. Скільки плитки, розмірами 1x1 потрібно, щоб викласти стіни і дно басейна ?
9.Басейн має розміри 15м, 8м і 1,8м. Скільки плитки, розмірами 1x1 потрібно, щоб викласти стіни і дно басейна ?
10. Визначити затрати керамічної плитки розміром (150x150) мм, для опорядження стін ванної кімнати розміром:
довжиною - Зм,
шириною - 2,5м,
висота панелі - 1,5м,
двері - (2x0,9) м.
11.Прямокутна кімната довжиною 5,6м, шириною Зм і висотою 2,5м обклеєна
шпалерами. В кімнаті є вікно шириною 2,3м і висотою 1,3м та 2 дверей шириною по
1,1м і висотою 2,1м. Скільки потрібно мати рулонів шпалер, якщо довжина кожного
рулону 10м і ширина 53 см?
12.Для оклеювання шпалерами стін кімнати використано 93,5м2 шпалер. Вік
на та двері займають 15,1м . Бордюр, яким обклеєні шпалери вздовж всіх стін, має
довжину 25,5м. Скільки буде коштувати фарбування підлоги цієї кімнати, якщо за
фарбування олійною фарбою кожного квадратного метра беруть 3 гривні і якщо ви
сота кімнати менша від її ширини на 1,42м?
13.Потрібно зацементувати підвал глибиною 2м, шириною 2,5м і довжиною
4м. Скільки потрібно використати для цього пудів цементу, якщо на кожний квадратний метр дна йде 2 пуди, а на квадратний метр стіни - 0,8 пуда цементу? (Підвал
має форму прямокутного паралелепіпеда). Міра. 1 тонна = 61 пуд.
14.Двосхилий дах має форму 3-гранної призми; дах простягається уздовж будинку на 21м, ушир - 8,5м, а висота даху (підйом) - 3,2м. Скільки м2 займає поверхня даху?
15.Прямокутника садиба, довжиною 153м, шириною 115м, обнесена парканом, який має висоту 213см. За скільки часу 4 малярі зможуть пофарбувати з двох
стін паркан з воротами та хвірткою, якщо 1 маляр фарбує за день 40,9м паркану?
16.Стайня довжиною 17м, шириною 11м, висотою від землі до даху - 496см, зроблена із цегли. В стайні знаходяться: 2 дверей висотою по 284см, шириною 195см; 6 вікон шириною по 709см, висотою по 355см. Скільки пішло цегли на стіни стайні, якщо на 1м2 стіни потрібно 198 штук цегли?
17.Яку масу мають 650 цеглин, якщо довжина кожної цеглини 24см, ширина-
12см, товщина-5см, р=1800кг/м.
18.Скільки цеглин потрібно для кладки 18 стовпів висотою 4м з перерізом у
вигляді квадрата зі стороною 7дм? Розмір цеглини 1дм х 1,5дм х 3 дм .Додати 5% на
злам.
19. Коридор має 21м довжини та 2,1м ширини й уміщує в собі 161м повітря.
Знайти висоту коридору.
20.Кубатура однієї кімнати будівлі дорівнює 120м3 . Обчислити кубатуру іншої кімнати, якщо її ширина в 1,5 рази більша від ширини першої , а довжина в З рази менша.
![]()
![]()
![]() 21. Для фундаменту кам'яної стіни, що оточує будинок (довжина будинку 383м, ширина-250м) потрібно викопати рів шириною 0,53м і глибиною 36см. За скільки годин зможуть виконати цю роботу 7 землекопів, якщо 3 землекопи за 13 годин викопають 19м землі, і якщо три хвіртки мають по 4,3 довжини?
21. Для фундаменту кам'яної стіни, що оточує будинок (довжина будинку 383м, ширина-250м) потрібно викопати рів шириною 0,53м і глибиною 36см. За скільки годин зможуть виконати цю роботу 7 землекопів, якщо 3 землекопи за 13 годин викопають 19м землі, і якщо три хвіртки мають по 4,3 довжини?
22. Підлога в прямокутному залі викладена мармуровими плитками. Кожна
плита має форму правильної 8-кутної призми зі стороною основи 6,4см і товщиною2,5см. Яку площу займає підлога , якщо маса всіх плит 89690кг?
23. Стіни та дно прямокутного басейну викладені плитами. Довжина басейну
101м, ширина -6,4м, а глибина -4,3м. Яка маса всіх плит, якщо на 1м2 поверхні басейну йде 313кг плит? Товщина плити 13см, а маса 1м3 плити 2352кг.
24. Проектується квартира з двох кімнат однакової ширини. Довжину першої хочуть зробити в 1,5 рази більшу від її ширини, а довжину другої кімнати - 7,2м. Знайти ширину кімнат, якщо площа двох кімнат повинна дорівнювати 56,7 м2.
25. Розміри бетонного блоку для будівництва стін такі: 2,7x1,4x0,5м. Порожнина блоку складає 20% його об'єму . Скільки потрібно бетону для виготовлення 450 таких блоків?
26. Скільки кілограмів покрівельного заліза завтовшки 1мм потрібно на покриття даху, який має форму правильної чотирикутної піраміди зі стороною 4,2 м при довжині схилу 6,5м? На шви та обрізки добавляється 10%. Розміри листа заліза 1400х700мм. Визначити кількість листів, витрачених на покриття даху.
27. Кабінет має розміри 6,5x4,8м і висоту 2,7м. Скільки листів дерево плити розміром 1,2x1,5м потрібно, щоб виготовити панелі, висота яких 1,2м? Двері мають ширину 1,5м.
28. Знайти площу пофарбованої поверхні і витрати олійної фарби при пофарбуванні дерев'яного ящика розміром по зовнішньому виміру 5,8x2,5x1,7 і по внутрішньому виміру 5,6x2,5x1,5м. Фарбування робиться з двох боків по два рази (якщо без кришки). На 1м2 витрачається 160 г фарби.
29. Потрібно обклеїти шпалерами кімнату розміром 5х4хЗм. Площа вікон і дверей складає 20% всієї площі стін. Скільки потрібно рулонів шпалер для обклеювання, якщо в рулоні 9м і ширина його 500мм?
30. Обчислити , скільки розчину необхідно для штукатурки кабінету розміром 6x9,5м при висоті Зм. Кабінет має три вікна розміром 2x1,6м і двері 1,3х2м. На 1м2 витрачається 0,02мл розчину.
31. Відро без кришки має форму зрізаного конуса з діаметрами 30мм і 20мм, а
твірна - 0,3м. Скільки потрібно взяти фарби для фарбування з обох боків 300 таких
відер, якщо на 1 м2 потрібно 160г фарби?
32. Знайти площу пофарбованої поверхні і витрати фарби для фарбування труб
діаметром 0,63м, довжина яких 86, 5 погонних метрів, діаметром 0,6 м- 174,75 погонних метрів. Фарбування виконується два рази. Витрати на 1м2 - 130г.
33. Потрібно приготувати цементно-вапняний розчин складу 1 : 0,5 : 6. Яку кількість складових компонентів у кубічних метрах необхідно взяти для приготування
1,2м2 розчину?
![]()
![]() 34. Скільки треба рулонів шпалер розміром 10x0,5м, щоб обклеїти кімнату
34. Скільки треба рулонів шпалер розміром 10x0,5м, щоб обклеїти кімнату
розміром 6x4,8x3,75? Кімната має 4 вікна розміром 1,8х0,75м. На підклейку витрачається 1%площі шпалер.
35. Дах водогінної вежі має форму правильної шестикутної піраміди, сторони
основи якої 2м, а бічне ребро 4,25м. Скільки потрібно листів заліза розміром 0,7х4м,
щоб покрити водонапірну вежу(відходи становлять 10% площі заліза)?
36. При шпаклюванні шпатель тримають під різними кутами до поверхні, яка
вирівнюється. Покажіть за допомогою шпателя кути, які утворюються. Якої величини вони допускаються, як залежить величина кута від товщини шару шпаклівки? Як
називаються такі кути в геометрії?
Тема. Тіла обертання
1 .Залізобетонна панель має розміри 600х120х22см. По усій її довжині - 6 циліндричних отворів, діаметри яких 14см. Знайти масу панелі, якщо густина матеріалу 2,5т/м3.
2. Зовнішній і внутрішній діаметри кільця для колодязя відповідно - 1,3м і 1,1м, а висота 0,9м. Скільки кубометрів бетону потрібно для виготовлення 8 таких кілець?
3. Скільки квадратних метрів паперу у рулоні шпалер , висота і радіуси якого відповідно 85см, 45см і 2см, якщо товщина паперу 0,1мм?
4. Потрібно поштукатурити дві колони однакової висоти, але з різним поперечним перерізом : круглим і квадратним. Зовнішній діаметр круглого перерізу і сторона зовнішнього квадрату дорівнюють 30см. На яку колону витратиться більше
штукатурки і у скільки разів?
5. При недотриманні норми товщини штукатурки допускається перевитрата
сировини і грошей. Підрахуйте, на скільки збільшиться вартість штукатурних робіт
при обробці стін приміщення (довжина -4м, ширина - 5м, висота – Зм ), якщо товщину
штукатурки збільшити на 2мм? на 5мм?( Примітка: вартість 1мм штукатурки на 1м2
становить ________ )
6. Скільки годин потрібно маляру для фарбування панелі висотою 2м в приміщені (дані попередньої задачі) щіткою і валиком , якщо норма часу для фарбування 100м поверхні щіткою -6,4год, валиком -3,4год.?
7. Чи можна використовувати формулу площі бічної поверхні призми для знаходження витрат: а) розчину, який іде на побілку стелі і стін; б) плиток, які потрібні
для покриття цоколя житлового приміщення. Відповідь обґрунтувати.
8. Наведіть приклади перекриття приміщень і споруд, які мають : а) призматичну; б) циліндричну; в) сферичну поверхню.
9.Виявилося, що маркування на технічні дані змішувачів розчину СО-80 і С-
368 стерлася. Які виміри необхідно виконати, щоб розрахувати об'єм розчину в бункері кожного змішувача? Яка з формул в цьому випадку знадобиться:
![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]() ?
?
![]() Тема. Об'єми геометричних тіл
Тема. Об'єми геометричних тіл
1.Яка різниця в об'ємі між глиняною звичайною цеглиною 250x120х65мм і модульною 250х120х88мм (силікатною) ?
2.Скільки кубічних метрів розчину витрачено на зовнішню штукатурку стін
будинку 65,5x14,5x20,8м? Будинок має 80 вікон розміром 1,6x2,25 і четверо дверей
1,5x2,5м. На один квадратний метр стіни витрачається 0,02м3 розчину. Дати відповідь з точністю до 0,1м.
3.На кутах листа заліза розміром 142x71см вирізано рівні квадрати із стороною 15см. Із загнутих країв виготовлено відкриту коробку. Знайти її об'єм.
4.Знайдіть висоту шару піску, якщо для засипки прямокутної площадки розмірами 4,0м і 6,9м було витрачено 13,8 куб. метрів піску.
Додаток 4











про публікацію авторської розробки
Додати розробку
