"Урок однієї задачі з геометрії". Обмін досвідом

Урок однієї задачі з геометрії.

Краще розв’язати задачу декількома способами,

ніж декілька задач - одним.

Д. Пойа

Основним засобом навчання математики є задачі. Вони виконують навчальну, розвивальну, виховну та контролюючу функції. Формування умінь розв’язувати задачі є однією з основних цілей навчання математиці.

Геометрія є одним із найскладнішим предметом для учнів, тому що для розв’язання потрібно знати велику кількість означень та теорем, а також застосовувати їх на практиці.

Уміння розв’язувати задачі є мистецтво, яке здобувається практикою. Будь - яка задача - це джерело інформації про конкретну ситуацію, аналіз якої грунтується на набутих знаннях.

Важливу роль у формуванні творчих здібностей учнів відіграють уроки - практикуми з розв’язування однієї задачі різними способами. Розв’язування задачі різними способами сприяє систематизації знань, умінь та навичок з різних розділів геометрії, дає змогу в окремих випадках змінити одне розв’язування іншим - легшим. Намагаючись знайти раціональний, оригінальний спосіб розв’язування задачі, учні згадують багато теоретичних фактів, вчаться аналізувати умову, логічно мислити, збагачують власний досвід застосування теоретичних знань в різних ситуаціях. Здійснюючи самостійний пошук різних способів розв’язування учні досягають міцних та глибоких знань. Усе це активізує навчально пізнавальну діяльність учнів, розвиває їх творчі здібності, стимулює активне, логічне мислення.

Урок однієї задачі - це урок, на якому йде пошук різних способів  розв’язання задачі. В учнів з’являється можливість знайти свій спосіб розв’язання, тобто той спосіб, який йому зрозумілий, в якому він може використати свої знання та вміння, але ж він почує різні міркування , побачить інші способи розв’язання цієї задачі. На цьому уроці вчитель формує особистість, яка може мислити, відстоювати свою думку, знаходити вихід із даної ситуації.

Розв’язування задачі різними способами привчає учнів самостійно висувати гіпотези і перевіряти їх, порівнювати результати, доходити висновків. Все це дуже важливе для майбутньої творчості, для наукової діяльності, а саме вміння знаходити неординарні шляхи вирішення проблем, знаходження можливості для самовираження, розуміння себе та інших, а в перспективі - розбиратись в людях, у житті. І це забезпечує успіх в будь - якій справі.

Приступаючи до розв’язування геометричної задачі, слід ураховувати, що майже кожна задача потребує індивідуального підходу, винахідливості та інтуіції. Вчитель на уроці формує особистість, яка спроможна міркувати, застосовувати свої знання на практиці, працювати самостійно.

 На уроці однієї задачі учні знайомляться зі специфікою того чи іншого способу розв’язування, його переваги та недоліки в залежності від вмісту задачі. В ході розв’язування задачі трапляється можливість побачити нові властивості, отримати цікаве узагальнення задачі. На цих уроках учні згадують багато теоретичного матеріалу, методи. прийоми, аналізують, порівнюють , проводять аналогію, накопичують певний досвід застосування одних і тих же знань до різних питань. Різні способи розв’язування задачі дозволяють виявити непередбачувані зв’язки між якимось віддаленими фактами та поняттями. Навчати дітей розв’язувати задачу різними способами треба поступово, використовуючі критерії:

1) правильність,

2) самостійність,

3) оригінальність.

Керівна роль вчителя під час пошуку інших способів розв’язування дуже важлива. Він сам повинен добре розв’язувати задачі, знати наперед , скількома способами можна знайти відповідь. Як правило, пошуки різних способів дуже зацікавлюють учнів, особливо здібних до математики. Інтерес - один із інструментів, який спонукає учнів до дослідницької діяльності, до більш глибокого пізнання предмету. Пошук іншого способу розв’язування приводить до встановлення нових зв’язків між величинами або використання відомих зв’язків у нових умовах.

Розглянемо приклад.

У рівнобедреному трикутнику основа дорівнює 12 см, бічна сторона - 10 см. Знайти висоту, проведену до бічної сторони.

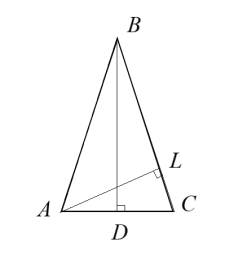
1) BD =

Трикутники ALC і BDC подібні, тому

2) Нехай LC = x . З трикутника ALB:  AL² = AB² - BL² .

З трикутника ALC: AL² = AC² - CL² .

Звідси: AB² - BL² = AC² - CL²

10² - (10 - х)² = 12² - х²;

100 - 100 + 20х - х² = 144 - х²;

20х = 144;

х = 7,2. Отже: LC = 7,2 см.

3) Розглянемо трикутник ALC, .

Тоді

Розглянемо задачу на доведення.

Якщо у трикутнику медіана вдвічи менша сторони, до якої вона проведена, то цей трикутник прямокутний.

Починаючи міркувати, учні намагаються згадати раніше вивчені положення, в яких говориться про перпендикулярність. Вони згадують про кут між бісектрисами суміжних кутів, теорему про кути при основі рівнобедреного трикутника.

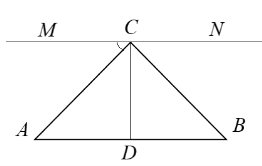
CD = 0,5АВ. Використовуючи той факт, що бісектриси двох суміжних кутів перпендикулярні, проведемо через точку С пряму MN, щоб утворилися два суміжних кути, бісектрисами яких були СА і СВ.

, тоді кути АСМ і А рівні, трикутник АCD - рівнобедрений (АD = CD), то кути АCD і А теж рівні. Звідси випливає, що кути АСМ і АCD рівні. отже СА - бісектриса кута МCD.

Аналогічно доводимо, що СВ - бісектриса кута NCD.

Кути МCD і NCD суміжні, то градусна міра кута АСВ дорівнює 90⁰.

2)

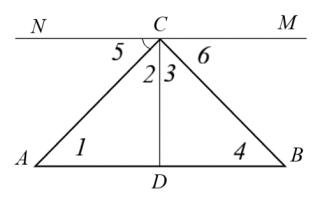
∠A+∠B+∠C =

∠1+∠2+∠3+∠4 =

Так як ∠1=∠2, ∠3=∠4, то

∠1+∠4=∠2+∠3

∠A+∠B+∠C=2(∠2+∠3)=2∠C=, ∠C=

3)

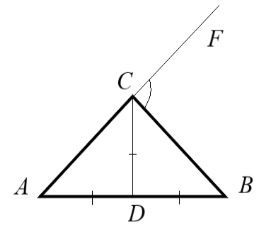
На промені АС відмітимо точку F. ∠FCB = ∠A+∠B.

∠FCB=∠ACD+∠BCD=∠ACB.

∠FCB=∠ACB=(суміжні)

Розв’язування задач різними способами створює прекрасні умови для розвитку логічного та креативного мислення учнів, для виховання в них вміння самостійно точно, правильно, коротко викладати свої думки.

Розв’язування задач різними способами потребує вміння застосовувати комплексно , отриманні раніше знання, а значить, це процес систематизації засвоєних учнями знань та вмінь.

При розв’язанні задач декількома способами розвивається гнучкість розуму, яка проявляється в умінні бачити нове у відомому, розвиває навички самоконтролю в учнів, так як відповідь при всіх знайдених способів розв’язання повинна бути однакова.

З’ясування того, хто  яким способом розв’язав і чий спосіб раціональний, може викликати великий інтерес і конкурентноспроможність учнів.

Досвід роботи в школі показує, що розв’язування задач різними способами гармонійно поєднується з процесом проведення уроку .Систематичне застосування цього прийому дає значний ефект як при навчанні розв’язування задач з геометрії, так і при навчанні курсу математики в цілому.

Робота вчителя - це постійний пошук та творчість.