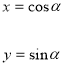Урок: "Основні співвідношення між тригонометричними функціями одного аргументу"

 

План-конспект уроку на тему:

«Основні співвідношення між тригонометричними функціями                           одного аргументу»

Мета уроку:     – домогтися розуміння учнями співвідношень між функціями

                              одного аргументу;

                           – формувати вміння застосовувати вивчені співвідношення для

                              тотожних перетворень виразів;

                           – знаходження значень тригонометричних функцій за даним

                              значеннями однієї з тригонометричних функцій.

Тип уроку:       засвоєння нових знань.

 

 

Хід уроку

 

І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ.

Оголошується тема сьогоднішнього уроку: Основні співвідношення між тригонометричними функціями одного аргумента.

ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ.

     Математичний диктант:

Записати, чому дорівнює:

1. cos30^o;
2. sin60^o;
3. tg30⁰;
4. cos45^o
5. ctg90^o;
6. sin45^o;
7. tg30⁰;
8. ctg0^o;
9. cos60^o
10. sin180^o.

Диктант проводиться із взаємоперевіркою. Після того, як учні обмінялися зошитами, на екран висвітлюються відповіді. За кожну правильну відповідь учень отримує один бал.

1.	cos30o
2.	sin60o
3.	tg300
4.	cos45o
5.	ctg90o	0
6.	sin45o
7.	tg600
8.	ctg0o	не існує
9.	cos60o
10.	sin180o	0

 

ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ.

Запитання до класу:

1. Запишіть у зошит основну тригонометричну тотожність.

()

2. Що називають косинусом кута α?

(косинусом кута повороту α називають абсцису х точки Р(х;у) одиничного кола, яку отримано з точки Р_о(1;0) у результаті повороту навколо початку координат на кут α)

3. Що називають синусом кута α?

(синусом кута повороту α називають ординату у точки Р(х;у) одиничного кола, яку отримано з точки Р_о(1;0) у результаті повороту навколо початку координат на кут α

4. Запишіть формулу для визначення відстані між двома точками, заданими своїми координатами.

()

 

ІV. ЗАСВОЄННЯ НОВИХ ЗНАНЬ.

На сьогоднішньому уроці ми повторимо і вивчимо шість основних співвідношень між тригонометричними функціями одного аргументу.

 

(1)-ше співвідношення.

 Основна тригонометрична тотожність відома учням ще з 9-го класу, але для аргументу від 0^о до 180^о. На сьогоднішньому уроці буде доведено дане співвідношення для довільного аргументу. (Даний етап уроку проводиться частково-пошуковим методом).

Запишемо умову:

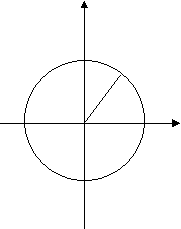
                                                                Дано: α – довільний числовий аргумент       

                        Довести:  .

                           

   -1                            1                                         

 

 

 

 

Міркування	Доведення
Виберемо довільну точку на одиничному колі.	- довільна точка одиничного кола.
Чому дорівнює квадрат довжини відрізка ?
Чим являється координати х і у на одиничному колі?	за означенням
	(1) Доведено.

 

(2)-ге та (3)-тє співвідношення.

Перед вами дві наступні формули. Як ми їх отримали?

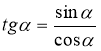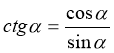  (2)                   (3)

(Використовуючи означення тангенса та котангенса.)

 

 

(4)-те співвідношення.

Виконаємо множення (2)-ї та (3)-ї тотожності (учні самостійно виконують множення):

,

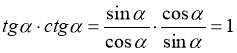таким чином, маємо ще одне співвідношення

      (4)

 

(5)-те та (6)-те співвідношення.

Для того, щоб отримати наступні співвідношення, виконаємо такі перетворення:

1. Поділимо обидві частини основної тригонометричної тотожності на :

        (5)

2. Самостійно доведіть (6)-те співвідношення

        (6)

(доведення аналогічне доведенню тотожності (5))

Таким чином, ми маємо шість основних співвідношень тригонометричних функцій одного аргументу.

 

V. ЗАКРІПЛЕННЯ НОВОГО МАТЕРІАЛУ.

1. Виконання усних вправ.

Завдання №1. Визначте, чи можуть одночасно виконуватися

                       рівності:

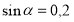1. і ;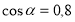

                                 (ні, тому що за формулою (1)  )

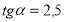2. і .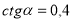

                                 (так, тому що за формулою (4) )

3. Чи можуть 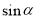  і 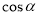одночасно дорівнюють  нулю?

(ні, тому що за формулою (1) 0² + 0² ≠ 1)

 

2. Виконання письмових вправ.

Основні тригонометричні тотожності застосовуються для обчислення значення тригонометричних функцій за відомим значенням однієї з них. Такі вправи учні виконували у 8-му класі, але в 10-му класі варто повторно з'ясувати їх розв'язання.

Завдання №2

 

Дано:

Обчислити:

Міркування	Розв'язання
1. Формула, яка пов'язує синус і косинус – це основна тригонометрична тотожність.
2. Виразимо
3. Як наслідок одержуємо
4. Враховуючи вказану чверть в умові задачі, вибираємо один з двох знаків, відповідний до знака синуса в цій  чверті.
	Відповідь:

 

 

Завдання №3

Якщо вправа вимагає за відомими значеннями однієї із тригонометричних функцій знайти значення решти, то необхідно, щоб учні спочатку виділили кроки розв’язання:

Дано:

Обчислити:

Алгоритм:            1. Знайти синус, скориставшись формулою:

                                         

                              2.Обчислити:

                                       

                              3. Знайти з тотожності:

                                     

Користуючись даним алгоритмом учні самостійно розв’язують завдання.

 

Наступними виконаємо вправи на перетворення тригонометричних виразів.

1. Найпростіші вправи, розраховані на використання лише однієї з тотожностей (репродуктивний рівень)

Завдання №4  Спростіть вираз:

а)

    .

б)

    .

в)

    

     .

2. Вправи, в яких використання однієї з основних тотожностей поєднується з застосуванням формул скороченого множення, дій з дробами, належать до реконструктивного рівня.

Завдання №5 Спростіть вираз:

Міркування	Перетворення
Розкриємо дужки, використавши формули квадрата суми та різниці двох виразів.
Зведемо подібні доданки
Винесемо спільний множник за дужки
Використаємо тотожність (5)

 

VІ. ПІДСУМОК УРОКУ.

Запитання до класу:

1. Які тотожності пов'язують між собою:

1. і ;
2. і ;
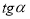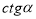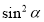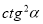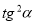3. і .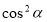

2. Знайдіть , якщо .

Отже, на сьогоднішньому уроці ми з вами згадали і вивчили основні співвідношення між трибометричними функціями одного аргументу. Для успішного виконання перетворень виразів необхідно вільно володіти тригонометричними тотожностями та формулами скороченого множення.

 

VІІ.ДОМАШНЄ ЗАВДАННЯ.