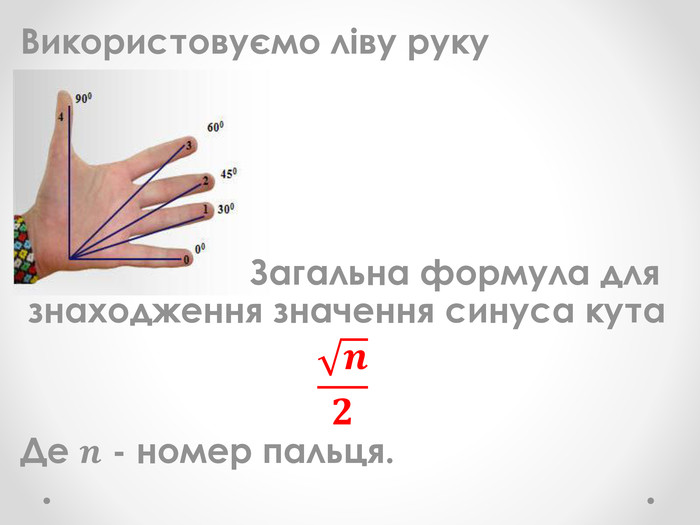
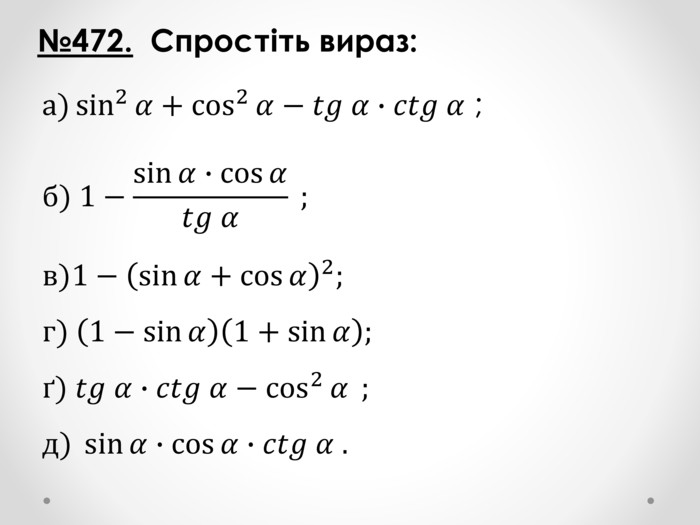Урок "Основні співвідношення між тригонометричними функціями одного аргументу"
Про матеріал
Розробка уроку. На початку кросворд, чітко і зрозуміло викладений матеріал. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку