Урок "Паралелепіпед"

Конспект уроку

Геометрія 11 клас

Тема: Паралелепіпед.

Мета:  засвоїти  означення: паралелепіпеда; прямого і похилого паралелепіпеда; Сформулювати властивості паралелепіпеда. Сформувати вміння розв’язувати задачі на застосування цих понять та властивостей.

Тип уроку: засвоєння знань, формування вмінь.

Наочність та обладнання: таблиця «Паралелепіпед», моделі паралелепіпедів, презентація.

 

Хід уроку

 

I. Організаційний етап

 

Перевірка готовності учнів до уроку, налаштування на роботу.

II. Перевірка домашнього завдання

 

Учитель збирає на перевірку зошити із виконаною самостійною роботою. У разі необхідності учні отримують правильні розв’язання цих вправ для самостійного опрацювання вдома.

III. Формулювання мети й завдань уроку

 

Сьогодні на уроці, ми ознайомимося з поняттям прямокутного паралелепіда та його елементами, знайдемо його у природі та навчимося обчислювати площі бічної та повної поверхні.

 

IV. Актуалізація опорних знань

 

Гра «Продовжити речення».

1) Многогранник – це тіло, складене з… (кінцевого числа плоских многокутників)

2) Многогранник, складений з двох плоских многокутників, які лежать в різних площинах, і всіх відрізків, які з’єднують точки цих многокутників, - це… (призма)             

3) Призма складається з таких елементів…

4) Основи призми…(паралельні та рівні)

5) Висота призми – це відстань між….( площинами основ)

6) Діагональ призми – це….( відстань між вершинами, які не належать одній грані)

7) Бічна поверхня призми – це…( сума площ бічних граней)

8) Площа повної поверхні призми дорівнює…

 

V. Засвоєння знань

 

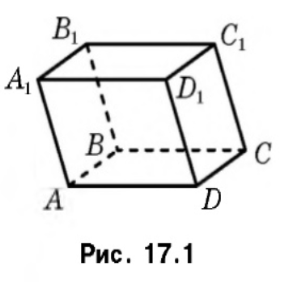Означення. Паралелепіпедом називають призму, основи якої є паралелограми.

На рис.17.1 зображено паралелепіпед . Будь яка грань паралелепіпеда є паралелограмом.

Дві несусідні грані паралелепіпеда називаються протилежними гранями паралелепіпеда. Наприклад, на рис.17.1 грані є протилежними.

Оскільки і (рис.17.1), то за ознакою паралельності площин .  Міркуючи аналогічно, можна довести, що будь-які протилежні грані паралелепіпеда лежать у паралельних площинах.

Паралелепіпед, бічні ребра якого перпендикулярні до площини основи, називають прямим паралелепіпедом.

Якщо бічні грані паралелепіпеда не перпендикулярні до площини основи, то паралелепіпед називають похилим.

Усі грані похилого паралелепіпеда — паралелограми (тому будь-яку грань паралелепіпеда можна вважати його основою).

Бічні грані прямого паралелепіпеда — прямокутники, а основи — паралелограми.

Грані паралелепіпеда, які не мають спільних вершин, називають протилежними.

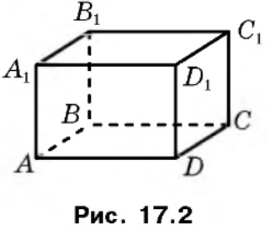
На рис.17.2 зображено прямокутний паралелепіпед .

Усі грані прямокутного паралелепіпеда є прямокутниками.

Правильна чотирикутна призма є окремим видом прямокутного паралелепіпеда.

 Довжини трьох ребер прямокутного папалелепіпеда, які виходять з однієї вершини, називають вимірами прямокутного паралелепіпеда. На рис. 17.2 довжини ребер AB, AD, AA₁ є вимірами прямокутного паралелепіпеда .

Прямокутний паралелепіпед називають кубом, якщо його виміри рівні.

 Усі грані куба є квадратами.

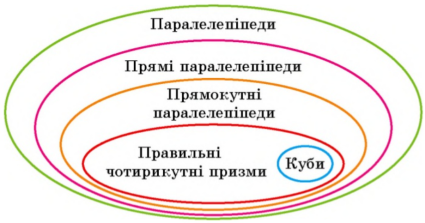
Зв'язок між паралелепіпедами та їхніми окремими випадками ілюструє схема, зображена на рис. 17.3.

 

Теорема: Квадрат будь-якої діагоналі прямокутного паралелепіпеда дорівнює сімі квадратів його вимірів.

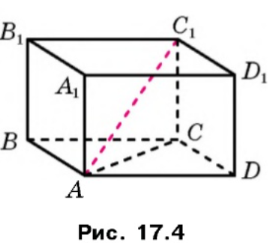Доведення: розглянемо діагональ AC₁ прямокутного паралелепіпеда   (рис.17.4).

Доведемо, що .

Оскільки трикутник ABC прямокутний (), то можна записати: . Оскільки BC=AD, то (1)

Даний паралелепіпед є прямокутним, тому .

Отже, ACC₁ прямокутний (ACC₁=90^о). Тоді . Оскільки CC₁=AA₁, то 

Ураховуючи рівність (1), можна записати:

.

Решта діагоналей доведення є аналогічним.

З теореми випливає, що діагоналі прямокутного паралелепіпеда рівні.

 

VI. Формування вмінь

 

Усно:

17.1. Чи можна вважати правильним таке означення куба: «Кубок називається правильна чотирикутна призма, висота якої дорівнює стороні основи»? ( Так)

17.2. Доведіть, що в прямокутному паралелепіпеді площина діагонального перерізу перпендикулярна до площини основи. ( Паралелепіпед прямий , якщо його бічні ребра перпендикулярні площині основи, тому площина діагонального перерізу перпендикулярна площині основи).

Письмово:

17.3. Сторони основи прямого паралелепіпеда дорівнюють 5 см і 24 см, а висота – 4 см. Знайдіть площу діагонального перерізу паралелепіпеда.

17.5. Знайдіть діагональ прямокутного паралелепіпеда, виміри якого дорівнюють 2 см, 3 см і 6 см.

Дано: а=2см, в=3см, с=6 см.

Знайти:d-?

17.7. Ребро куба дорівнює а. Чому дорівнює діагональ куба? 

Дано: куб, а=а.

Знайти: d-?

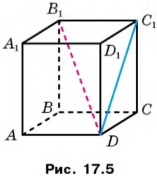17.9. Дано прямокутний паралелепіпед (рис17.5), АВ=5 см, AD=7 см,  AA₁=12 см. Знайдіть кут:

1) між прямими DC₁ і площиною ACC₁;

2) між прямою В₁D і площиною ABB₁.

17.12. Основа прямого паралелепіпеда – ромб з гострим кутом a і меншою діагоналлю d.  Більша діагональ паралелепіпеда утворює з площиною основи кут . Знайдіть площу бічної поверхні паралелепіпеда.

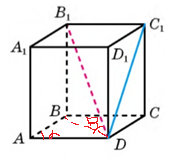Дано: BD=d,

Знайти: S_{б =}-?

1)

2)

 

 

 

3)

17.17. Основа ABCD паралелепіпеда є квадратом.

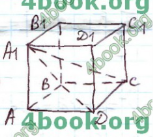Вершина A₁ рівновіддалена від усіх вершин основи ABCD. Знайдіть висоту паралелепіпеда, якщо сторона основи дорівнює 8 см, а бічне ребро паралелепіпеда – 6 см.

Дано: АD=8см, AA₁=6cм.

Знайти: h-?

AA₁=A₁B=A₁C=A₁D=6 cм

h=2см.

 

VII. Підсумки уроку

 

Контрольні запитання

1. Сформулюйте означення паралелепіпеда.

2. Сформулюйте основні властивості паралелепіпеда.

3. Який паралелепіпед називають похилим; прямим?

4. Укажіть, які з наведених тверджень правильні:

1) бічне ребро паралелепіпеда перпендикулярне до діагоналей основи;

2) у прямому паралелепіпеді бічне ребро перпендикулярне до сторін основи;

3) усі діагоналі прямого паралелепіпеда рівні.

 

VIII. Домашнє завдання:

 

 § 17, № 17.4, 17.6, 17.8, 17. 10, 17.18.