Урок. Перерізи многогранників

 

Методична розробка уроку

 

Клас 11

Предмет  Геометрія

Тема уроку  Перерізи многогранників

Мета уроку  Ознайомити учнів з перерізами многогранників. Формування в учнів умінь побудови перерізів многогранників. 

           

Хід уроку

 

Побудова перерізів многогранників площинами.

Обґрунтування форми перерізу.

В стереометрії часто доводиться розглядати перерізи тіл, зокрема многогранників, різними площинами. Переріз опуклого многогранника є опуклий плоский многокутник. Його вершини в загальному випадку є точками перетину січної площини з ребрами многогранника, а сторони – відрізками, по яких січна площина перетинає грані многогранника.

Задачі на перерізи многогранника площиною зазвичай полягають в тому, щоб побудувати паралельну проекцію самого многогранника і умови, за допомогою яких задається січна площина, і обчислити площу одержаного перерізу або відношення, в якому січна площина поділяє об'єм многогранника. Розв'язання кожної з двох частин такої задачі має бути переконливо обґрунтовано.

В залежності від взаємного розташування многогранника і січної площини переріз може бути трикутником, чотирикутником, тощо, одначе число сторін многокутника-перерізу не може перебільшувати числа всіх граней даного многогранника. Наприклад, перерізи куба площиною можуть мати форму трикутника, чотирикутника, п'ятикутника, шестикутника, при чому кожен з цих видів перерізів може утворитися в різних варіантах (наприклад, трикутник правильний, рівнобедрений, різносторонній).

При побудові перерізу многогранника площиною, незалежно від методу побудови, потрібно розв'язати дві задачі: будувати точку перетину прямої (ребра) січною площиною і лінію перетину двох площин (січної площини і площини грані). Обидві ці задачі було розглянуто детально раніше, лишається домогтися від кожного глибокого та міцного засвоєння цих елементарних побудов.

Побудова перерізу многогранника площиною, що задана трьома точками.

ЗАДАЧА 1. Побудувати переріз прямокутного паралелепіпеда площиною, що проходить через три точки на ребрах, що виходять з даної вершини.

ПОБУДОВА

Нехай дано зображення прямокутного паралелепіпеда ABCDA₁B₁C₁D₁. В умові задачі січна площина задана трьома точками на ребрах, що виходять з однієї вершини (мал.1). Для зручності візьмемо за таку вершину точку В₁. Отже, точки МА₁В₁, NB₁C₁, KBB₁ є даними. Оскільки кожні дві з них належать до однієї з граней даного многогранника, їх можна сполучити відрізками MN, МК і NK. Утворився трикутник MNK, який с шуканим перерізом.

 

 

 

 

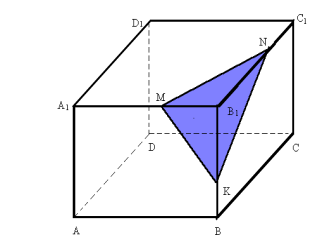
Мал1

 

ЗАДАЧА 2. Побудувати переріз призми площиною, що проходить через точки М, N та К на бічних ребрах.

Нехай маємо зображення даної призми ABCDA₁B₁C₁D₁ (мал.2) з даними точками на ребрах: М АА₁, N ВВ₁, К СС₁. Щоб побудувати шуканий переріз, потрібно знайти точку, що належить ребру DD₁. Для цього спочатку з'єднаємо відрізками точки  М і N, N і К, що лежать на бічних ребрах даного тіла та точки М і К, оскільки вони належать до площини діагонального перерізу АСС₁А₁. Проведемо також другий діагональний переріз BDD₁B₁, який перетинається з площиною по прямій ОО₁ де точки О і О₁ – спільні точки діагоналей основ АС та BD, A₁C₁ та B₁D₁ відповідно. Відрізок МК перетинає цю пряму у точці F. Отже, пряма NF належить січній площині за теоремою про належність прямої до площини. Ця пряма (NF) перетинає ребро DD₁ у точці Р. Тоді точка Р лежить в одній площині з точкою М, а також з точкою К.

 

 

 

 

 

 

Мал.2

Утворилися відрізки МР і КР, що також є сторонами перерізу. Отже, перерізом є чотирикутник MNKP.

На малюнку 3 розв'язано подібну задачу для п'ятикутної призми.

Мал.3

ЗАДАЧА 3. Побудувати переріз призми площиною, що задана точками на трьох різних гранях.

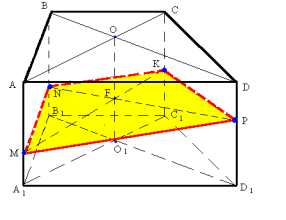
Нехай на мал.4 маємо зображення призми ABCDA₁В₁C₁D₁ з точками М, N і Р на бічних гранях. Для побудови перерізу, що проходить через точки М, N і Р скористуємося методом побудови сліду перетину площини (MNP) з площиною основи призми, одержимо точки М₁, N₁ і Р₁ відповідно. Знайдемо точку Е – точку перетину прямих NP та N₁P₁ і точку F – спільну точку прямих NM та N₁M₁. Пряма EF – слід  перетину січної площини з площиною основи призми. Пряма CD, що є проекцією прямої, яка проходить через точку М і належить грані DCC₁D₁, перетинається з прямою EF у точці Н, отже, це пряма МН. Вона перетинає ребра призми у точках S і L. Аналогічно знаходимо точки К і Т на ребрах АА₁ і ВВ₁.

 

 

 

 

 

 

Мал.4

Отже, чотирикутник SLKT - шуканий переріз, сторони якого проходять через задані точки М, N і Р.

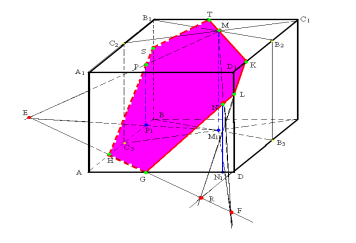
ЗАДАЧА 4. Побудувати переріз призми площиною, що задана двома точками на бічних гранях і точкою на верхній грані.

ПОБУДОВА

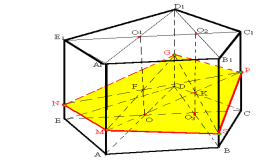
Нехай на мал.5 зображено дану призму ABCDA₁B₁C₁D₁ з точками N і Р на бічних гранях і точкою М на верхній грані призми. Щоб побудувати шуканий переріз, знайдемо проекції даних точок на площину основи. Точки Р1 і N1 – проекції  точок Р і N відповідно. Щоб знайти проекцію точки М, проведемо прямі С1М і В1М у верхній площині і паралельні їм відповідні СС3 і ВВ3, спільна точка яких М1 і є проекцією точки М. Прямі M1P1 і МР перетинаються у точці Е, прямі M1N1 і MN – у точці F. Отже, пряма EF – спільна пряма січної площини і площини основи. На мал.7 вона перетинає

сторону основи у точках G і Н. Відрізки HS (що проходить через точку Р) і GL (що проходить через точку N) є сторонами шуканого перерізу. Січна площина перетинає площини основи по паралельних прямих, тому проведемо через точку М пряму КТ, паралельну прямій EF. З'єднаємо точки S і Т, L і К.

 

 

 

 

 

 

 

 

Мал.5

Шестикутник GLKTSH – шуканий  переріз.

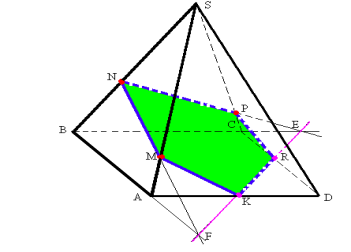
ЗАДАЧА 5. Побудувати переріз піраміди площиною, що проходить через три точки на її бічних ребрах.

ПОБУДОВА

Нехай на мал. 6 дано зображення піраміди SABCD з точками М, N і Р на її бічних ребрах SA, SB і SC відповідно. Через ці точки проходить січна площина, отже, вона перетинає бічні грані SAB і SBC по відрізках MN і NP відповідно.

 

 

 

 

 

 

 

 

Мал.6

При внутрішньому центральному проектуванні з центром у вершині піраміди S точка М переходить у точку А, точка N – у точку В, точка Р – у точку С. Тоді січна площина перетинає площину основи піраміди по прямій EF, де точка F – спільна точка прямих MN і АВ, точка Е – спільна точка прямих NP і ВС. Ця площина перетинає основу піраміди по відрізку KR. Отже, п'ятикутник KMNPR – шуканий переріз.

 

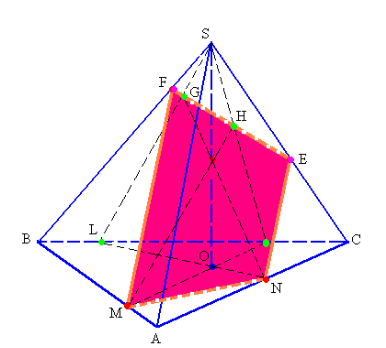
ЗАДАЧА 6. Побудувати переріз трикутної піраміди площиною, що проходить через дві точки, що лежать на сторонах основи та точку, взяту на висоті піраміди.

Нехай на мал. 7 дано зображення трикутної піраміди SABC з висотою SO. Дано три точки: М  АВ, N  AC, K  SO. Переріз піраміди площиною буде мати спільні точки з ребрами BS та CS. Треба відшукати їх. Площина МОК перетинає грань BSC по відрізку SP, а пряма МК площини МОК – у  точці Н (Н = SP  MK). Площина NOK перетинає грань ВSС по відрізку SL, пряма NK цієї площини – точці  G (G = SL  NK). Отже, пряма GH, що лежить одночасно у січній площині та у грані BCS, перетинає ребра BS і CS у точках F і Е відповідно.

 

 

 

 

 

 

 

 

 

 

 

 

 

Мал.7

Тому чотирикутник MNEF є шуканим перерізом.

Задання січної площини прямою і точкою поза нею, двома прямими, що перетинаються, або двома паралельними прямими рівносильне визначенню цієї площини трьома точками, що не лежать на одній прямій. При цьому, у ряді випадків побудова перерізу полегшується, тому, що ми одразу отримуємо 2-4 вершини многокутника – перерізу.

Розглянемо кілька задач.

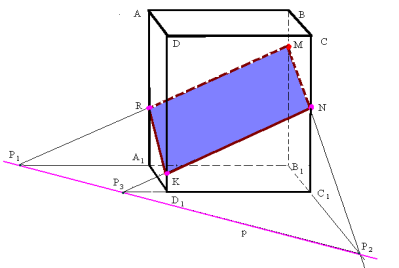
ЗАДАЧА 7. Побудувати переріз призми площиною, що проходить через точку М на бічному ребрі і має слід на площині основи пряму р, яка не перетинає основу призми.

ПОБУДОВА

Нехай маємо (мал.8) зображення призми ABCDA₁B₁C₁D₁, а також задану точку М на ребрі ВВ₁ та пряму р на площині A₁B₁C₁D₁ причому вона не перетинає ребра основи.

Для побудови перерізу потрібно знайти точки, що належать ребрам АА₁ СС₁ і DD₁. У цих точках січна площина має перетинати дані ребра. Міркуємо так: пряма A₁B₁ є проекцією сторони перерізу на основу. Продовжимо A₁B₁ до перетину з прямою р у точці Р₁. Пряма МР₁ перетинає ребро АА₁ у точці R. MR – сторона, шуканого перерізу.

Аналогічно будуємо точку N на ребрі СС₁ (Р₂ = В₁С₁  р) (N = ВР₂  МР₂). Продовжимо ребро C₁D₁ до перетину з прямою р у точці Р₃, а потім проведемо пряму NP₃, яка перетинає ребро DD₁ у точці К. Отже, точки М, N, К і R належать січній площині і ребрам даної призми.

 

Таким чином чотирикутник MNKR і є шуканим перерізом.

 

 

 

 

 

 

 

 

 

 

 

Мал.8

 

ЗАДАЧА 8. Побудувати переріз призми площиною, що проходить через точку М на верхній основі та має слід з нижньою основою – пряму р, яка не перетинає основи призми.

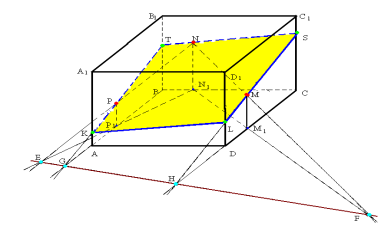
Нехай маємо (мал.9) зображення даної призми ABCDA₁B₁C₁D₁, яку січна площина перетинає у точці М на верхній основі і по прямій р у площині нижньої основи. Ми повинні знайти всі точки, по яких ця січна площина перетинає ребра призми. Оскільки площини ABCD (яка містить М) і A₁B₁C₁D₁ – паралельні грані даної призми, бо є основами призми, то пряма, по якій січна площина перетинає грань ABCD, має проходити через точку М і бути паралельною прямій р (за властивістю паралельних площин). Проведемо її. Вона перетинає ребра АВ і ВС у точках R і К відповідно. Пряма A₁B₁ є проекцією прямої січної площини, яка проходить через точку R і перетинає ребро АА₁. Продовжимо A₁B₁ до перетину з слідом р у точці Р₂ і з'єднаємо точки R і Р₂ . Пряма P₂R перетинає АА₁ у точці S. Аналогічно одержимо точку N на ребрі СС₁. Отже, RS та KN – ще дві сторони шуканого перерізу.

Оскільки січна площина перетинає ребро DD₁ у точці, яку ми назвемо Т, то її знайти дуже легко: продовжимо ребро C₁D₁ до перетину з прямою р у точці Р₃, а потім з'єднаємо точки N і Р₃ Пряма NP₃ що лежить у площині грані DCC₁D₁ перетинає ребро DD₁ у шуканій точці Т. Лишилося з'єднати точку Т з точками S і N. Таким чином, п'ятикутник KNTSR – є  шуканим перерізом.

 

 

 

 

 

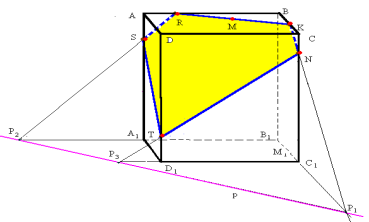
Мал.9

 

ЗАДАЧА 9. Побудувати переріз піраміди площиною, що проходить через точку М на бічній грані і має слід з площиною основи – пряму р у площині основи, яка не перетинає сторони основи.

ПОБУДОВА

Нехай на мал.10 дано зображення піраміди SABC, яку січна площина перетинає у точці М на грані ASB . Відомо також, що січна площина проходить через пряму р на площині основи піраміди, пряма р не має з основою спільних точок.

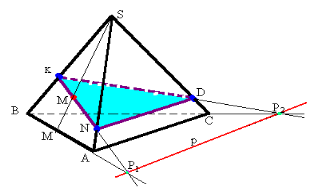Міркуємо так: якщо січна площина має спільну точку з гранню ASB, то вона перетинає її по прямій, що проходить через цю точку. А при центральному проектуванні з центром S ця пряма матиме проекцією пряму АВ на площині основи. Тому продовжимо АВ до перетину з слідом р у точці P₁ і проведемо пряму MP₁, яка перетинає ребра SB і SA у точках К і N відповідно. Аналогічно будуємо точку D на ребрі SC (D = КР₂  SC₁, а Р₂ =ВС  р). Точки N, К і D є вершинами трикутника NKD – який  і є шуканим перерізом.

Мал.10

 

 

 

 

 

 

ЗАДАЧА 10. Побудувати переріз піраміди площиною, що проходить через точку М на бічному ребрі та має слід з площиною основи – пряму р, що не перетинає сторін основи.

Нехай на мал.11 дано зображення чотирикутної піраміди SABCD , точка М на ребрі SA та пряма р на площині основи піраміди, яка не перетинає сторони основи. Для побудови шуканого перерізу, знайдемо точки на ребрах SB, SC та SD. Якщо точка N належить ребру SD, то при внутрішньому центральному проектуванні AD є проекцією MN на площину основи, а точка Р₁, у якій перетинаються пряма AD і слід р, – є  спільною точкою прямої MN і площини основи. З'єднаємо точки Р₁ і М, пряма Р₁М перетинає ребро у точці N. Аналогічно знайдемо точку R на ребрі SC і точку Т на ребрі SB. Чотирикутник MNRT – шуканий переріз.

 

 

 

 

 

 

 

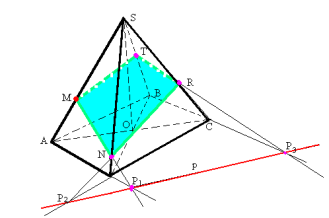
Мал.11