«Властивість бісектриси трикутника» для узагальнення даної теми при підготовці до ДПА і ЗНО з математики.

Тема : «Властивість бісектриси трикутника»

для узагальнення даної теми при підготовці до ДПА і ЗНО з математики.

Пояснювальна записка

            Дана розробка призначена для повторення деяких тем планіметрії, що входять до тематичного плану вивчення геометрії в 8 класі .

        У цій роботі розглядається одна з тем, за якими розроблені такі ж навчально-методичні матеріали, які містять в собі теоретичні факти, завдання різного рівня складності з рішеннями і добірка завдань для учнів з метою більш якісного закріплення матеріалу. Їх можна також використовувати для домашнього завдання або контролю знань. За навчальним часу заняття може бути організовано для 1-3 уроків, в залежності від рівня підготовки учнів.

Про трикутники цікаве

Кожен старшокласник вчить.

На якихось три кути

Йдуть століття – не роки!

І. Організаційний  момент: постановка теми і мети уроку

(Мотивація). Історично геометрія починалася з трикутника, тому ось уже два з половиною тисячоліття трикутник є символом геометрії. Без перебільшення можна сказати, що вся або майже вся геометрія будується на трикутнику.     Дивно, але трикутник, незважаючи на свою уявну простоту, є невичерпним об'єктом вивчення – ніхто, навіть в наш час не наважиться сказати, що вивчив і знає все властивості трикутника.

ІІ. Актуалізація опорних знань

А які трикутники ми з вами розглядали?  (Очікувані відповіді: рівнобедрений, рівносторонній, різносторонній, тупокутний, прямокутний, гострокутний). Сьогодні ми з вами дуже коротко ознайомимося з трикутниками, які мають своє власне «ім'я», або носять ім'я того, хто їх відкрив або досліджував. Єгипетський трикутник - прямокутний трикутник із співвідношенням сторін 3: 4: 5. Єгипетський трикутник із співвідношенням сторін 3: 4: 5 застосовувався єгиптянами - землемірами і архітекторами для побудови прямих кутів. Незважаючи на вік, це спосіб побудови прямого кута активно використовується будівельниками і тепер. Трикутник Паскаля такий простий, що побудувати його зможе навіть десятирічна дитина. У той же час він таїть в собі невичерпні скарби і пов'язує воєдино різні аспекти математики, що не мають на перший погляд між собою нічого спільного. Трикутник Рело - це геометрична фігура, утворена перетином трьох рівних кіл однакового радіуса з центрами в вершинах рівностороннього трикутника. Свердло, зроблене на основі трикутника Рело, дозволяє свердлити квадратні отвори (з неточністю в 2%). Один з найзагадковіших і цікавих трикутників - "Бермудський трикутник". Ще це місце називають аномальною зоною. Насправді це місце, яке традиційно вважається найжахливішим, найстрашнішим місцем планети. Тут безслідно зникала безліч кораблів і літаків - більшість з них після 1945 року. Тут загинуло більше тисячі чоловік. Однак при пошуках нікого і нічого не вдалося виявити. Бермудський трикутник не має чітких меж, не можна знайти на карті його точне позначення. Трикутник Пенроуза — одна з  основних неможливих фігур, відома також під назвами неможливий трикутник. Був відкритий в 1934 році шведським художником Оскаром Реутерсвардом, який зобразив його у вигляді набору кубиків. У 1980 році цей варіант неможливого трикутника був надрукований на шведських поштових марках .

Які лінії в трикутнику можна провести?

• Висоту (перпендикуляр, який проведений з вершини трикутника на протилежну сторону).
• Медіану ( відрізок, який з’єднує вершину трикутника з серединою протилежної сторони).
• Бісектриса (промінь, що проходить через вершину кута і ділить його навпіл)

Усна фронтальна робота з узагальнення теоретичного матеріалу.

Які з наступних тверджень вірні?

• Бісектриса завжди проходить через середину сторони трикутника.
• Будь-яка бісектриса рівнобедреного трикутника є його медіаною.
• Бісектриса рівнобедреного трикутника, проведена з вершини, протилежної основи, ділить основу на дві рівні частини.
• Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам.
• Бісектриса завжди проходить через середину сторони трикутника.
• Будь-яка бісектриса рівнобедреного трикутника є його медіаною.
• Бісектриса рівнобедреного трикутника, проведена з вершини, протилежної до основи, ділить основу на дві рівні частини.
• Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам.

Визначення теми уроку і постановка цілей уроку спільно з учнями.

ВЛАСТИВОСТІ    БІСЕКТРИСИ    КУТА    ТРИКУТНИКА

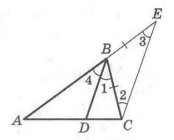    Однією з цікавих властивостей бісектриси кута трикутника, про яку інколи забувають абітурієнти, є поділ сторони на відрізки пропорційні бічним сторонам.

    На даному малюнку наведено й доведення цієї властивості.

Отже, теорема:

1. Бісектриса кута трикутника ділить сторону. до якої вона проведена, на відрізки, пропорційні прилеглим до них сторонам.

Тобто: АD:DC=AB:BC

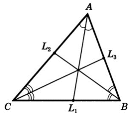
2. Бісектриси трикутника перетинаються в одній точці.

3. Бісектриса кута паралелограма відсікає рівнобедрений трикутник

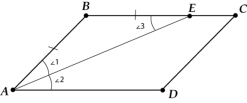
4. Бісектриси кутів, прилеглих до однієї сторони паралелограма і трапеції перетинаються під прямим кутом.

ІІІ. Закріплення навчального матеріалу розглянемо на прикладі рішення

деяких завдань.

Завдання № 1

Сторони трикутника дорівнюють 10 см, 11 см і 12 см. Знайти відрізки, на які ділить бісектриса трикутника середню сторону.

Дано: AC = 10 см, BC = 11 см, AB = 12 см, AP = бісектриса.

Знайти: CP і BP.

Розв’язання:

По властивості бісектриси трикутника:    

Нехай CP=x см, тоді  BP=11-x см:

        За основною властивістю пропорції маємо:

CP=5 см, BP=6 см.

Відповідь: 5 см, 6 см.

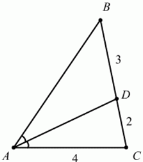Задача № 2

У трикутника ABC проведена бісектриса AD. Знайти периметр трикутника ABC,

якщо АС = 4см; DC = 2см; BD = 3см.

Розв’язання:

За властивістю бісектриси BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.

Периметр трикутника АВС Р= 6 + 5 + 4 = 15 см.

Відповідь: 15 см.

Задача №3

У прямокутному трикутнику бісектриса гострого кута ділить протилежний катет на відрізки 20 см і 12 см. Обчислити периметр трикутника.

Розв’язання: Оскільки катет ділиться бісектрисою на відрізки 20см та 12 см, то довжина гіпотенузи відноситься до довжини іншого катета як 20:12=5:3. Нехай гіпотенуза АВ=5к, катет ВС=3к, складемо рівняння за теоремою Піфагора:

25k²=9k²+32²

к=8, 5к=40, 3к=24.

Отже Р=24+40+32=96(см)

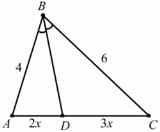Задача №4

Дано трикутник ABC, в якому  BD - бісектриса . АВ = 4 см, ВС = 6 см. АD : DС = 2 : 3. Знайти довжини відрізків, на які розділяє бісектриса сторону АС.

Розв’язання: за властивістю бісектриси AD/DC = AB/BC = 4/6 = 2/3.

Нехай AD = 2х; DC = Зх. Складемо пропорцію:

;                         12х = 12х;    х =1.

АD = 2·1 = 2см; DС = 3 · 1 = 1см.

Протягом декількох років серед завдань ЗНО не раз пропонувалися планіметричних задачі, які в разі застосування цієї властивості вирішувалися б простіше. Розглянемо кілька прикладів таких завдань.

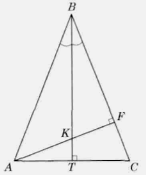Задача 1. В рівнобедреному трикутнику ABC с основою АС проведено висоти ВТ и AF. Вони перетинаються в точці К. Відомо, що АВ = 15 см, АК= 5 см. Знайти  площу трикутника АВК (рис. 1).

Розв’язання. Так як висота ВТ, проведена до основи рівнобедреного трикутника ABC, є бісектрисою кута В, то відрізок ВК - бісектриса кута В ​​трикутника ABF. За властивості бісектриси трикутника:

      звідки                                            

Нехай  KF= х, тоді BF = Зх, AF = = 5 + х. Розглянемо трикутник ABF. За теоремою Піфагора , де AF = AK + KF.

Маємо: 225=   ,  .  Отже, BF = 3х = 3 • 4 = 12.

Звідси,          

Задача 2.

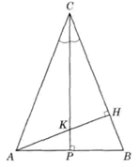Площа рівнобедреного трикутника ABC дорівнює 90, а бічна сторона дорівнює 10 . До основи АВ і стороні ВС проведено висоти СР і АН відповідно, які перетинаються  в точці К. Знайдіть площу трикутника СКН .

Розв’язання:

Звідки  sin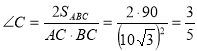 

Розглянемо трикутник АСН. У ньому АН = . За теоремою Піфагора 

Так як висота СР, проведена до основи рівнобедреного трикутника ABC, є бісектрисою кута С, то відрізок СК - бісектриса кута С трикутника АСН. За властивістю бісектриси трикутника маємо:

Нехай  АК = 5х і КН = 4х. Тоді:

9х=6 , х= , КН = .

Таким чином,

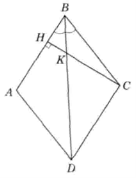Відповідь: 32

Задача 3.

Дано ромб ABCD з гострим кутом В. Площа ромба дорівнює , а синус кута В ​​дорівнює . Висота СН перетинає діагональ BD в точці К. Знайдіть довжину відрізка СК.

Розв’язання:

Так як діагональ ромба є бісектрисою його кута, то BD - бісектриса кута В, а значить, ВК - бісектриса кута В ​​трикутника НВС. Далі знаходимо сторону і висоту ромба.

Площа ромба: , з формули площі шукаємо сторону ромба:

;    ;    .

Також площу ромба можна знайти за формулою:  ,

де h=. В прямокутному трикутнику ВСН

Нехай НК = х, КС = 4 –х. За властивістю бісектриси маємо:

;     ;  х = 1. СК = 4 – 1 = 3.

Відповідь: СК = 3.

ІV. Домашнє завдання

• Повторити  зміст теореми о властивості бісектриси трикутника.
• Розв'язати задачі:

1. Бісектриса рівнобедреного трикутника ділить бічну сторону на відрізки завдовжки 2 см і 4 см, починаючи від основи трикутника. Знайдіть основу трикутника.

2. Бісектриса прямокутного трикутника ділить гіпотенузу на відрізки, різниця яких складає 5 см. Знайдіть сторони трикутника, якщо відношення катетів дорівнює 3 : 4.

3. Бісектриса кута при основі рівнобедреного трикутника ділить висоту, проведену до основи, на відрізки завдовжки 16,5 см і 27,5 см. Знайдіть відрізки, на які ця бісектриса ділить бічну сторону трикутника.

Повторити теорему про вписані кути та її наслідки.