Урок "Перетворення графіків функції у = f(x)+b, y=f(x-a). Розв’язування вправ"

Тема уроку: Перетворення графіків функції у = f(x)+b,

y=f(x-a). Розв’язування вправ

Цілі:

• Формування предметних компетентностей: сформувати вміння виконувати перетворення графіків функцій у = f(x)+b, y=f(x-a).
• Формування ключових компетентностей:

• формувати вміння аналізувати, прогнозувати, ухвалювати оптимальні рішення;
• формувати графічну культуру учнів;
• формувати вміння аргументувати та відстоювати власну позицію; висловлювати власну думку, слухати і чути інших;
• сприяти самовихованню старанності, охайності, чесності, самокритичності.

Тип уроку:  урок засвоєння нових знань.

Наочність та обладнання: презентація  до уроку, мультимедійний комплекс,  ППЗ  «Алгебра  7-11 клас».

Епіграф

“ Немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення “

К.Ф.Лебединцев

                                                         Хід уроку

1. Організаційний  момент
2. Актуалізація знань учнів

1. Теоретична розминка

Кросворд

«Математичне намисто»

1. Як називають геометричну фігуру, яка складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати – значенням функції? (графік)
2. Як називають значення аргументу, при якому значення функції дорівнює 0? (нулі)
3. Як називається функція, якщо для будь – якого х з області визначення f(-x) = f(x)   (парна)
4. Проміжок, на якому функція не змінює свій знак називається проміжком …. (знакосталості)
5. Функція виду y = kx називається …(пряма пропорційність)
6. Якщо на деякому проміжку f(x₀)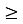f(x), то значення f(x₀) називається … (найбільше)
7. f(x₀) – це …. (значення) функції в точці x₀
   2. Відомості про графіки  (рис. 1)

               

 

 

   

 

 

   

 

   

 

 

   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

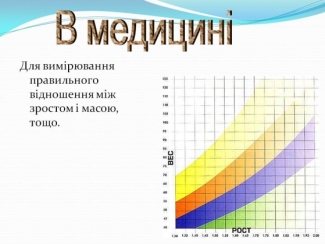
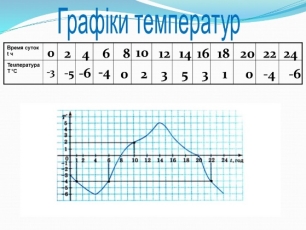
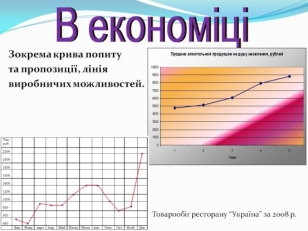
Рис. 1

 

3. Задати формулою функцію та назвати її властивості (рис. 2)

 

   

 

  

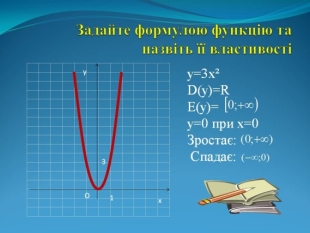
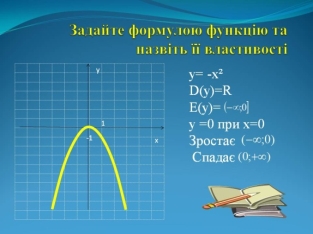
Рис. 2

 

4. Математичний диктант (із подальшою  взаємоперевіркою)  (рис. 3)

 

  

 

  

 

  

 

  

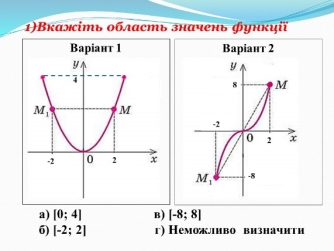
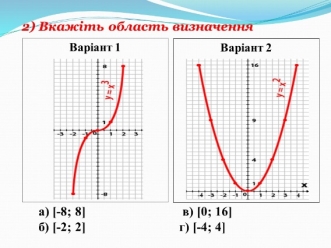
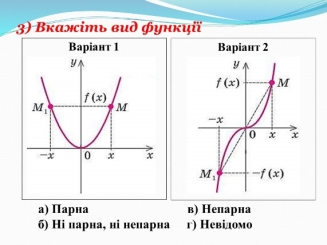
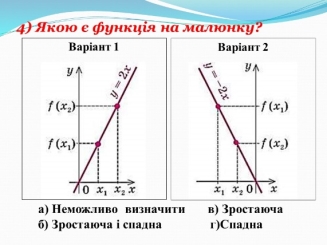
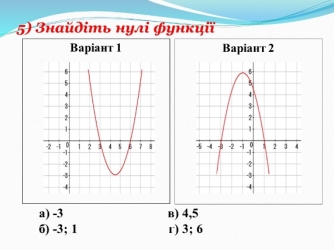
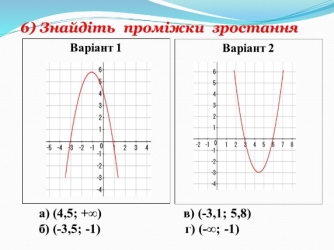
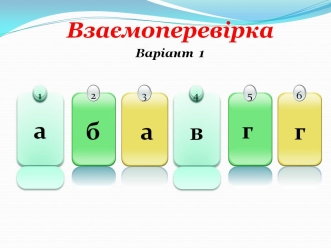
Рис. 3

 

5. Практичне застосування квадратичної функції

Задача  

Міст заввишки 2 м має форму параболи. Основи мосту знаходяться на відстані 24 м одна від одної. Міст тримають п’ять колон, що знаходяться на однаковій відстані одна від одної. Знайти висоту кожної колони.

Розв’язання

Зобразимо міст в прямокутній системі координат (рис. 4).

  

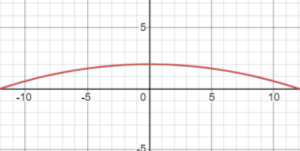
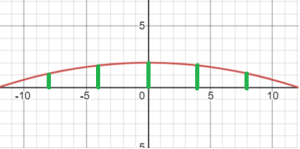
Рис. 4

Оскільки колон п’ять, то вони ділять відстань між основами на шість рівних частин, кожна з яких складає 4 м. Рівняння параболи .

Знайдемо коефіцієнти. При , . Отже .      при .

Вершина параболи знаходиться за формулою ₀=. Оскільки ₀=0, то b=0.

,  Оскільки b=0 і , то . Підставимо замість x числове значення .

,

,

.

Тоді наша функція набуде вигляду   . 

Знайдемо значення функції в точках: -8; -4; 4; 8.

 

 

 

 

 

Отже , висоти колон   м,   м, 2 м,   м,   м.

 

3. Пояснення нового матеріалу

1. Побудуємо графіки функцій   у = 2х²   та у = 2х² +1  (рис. 5).

 

  

 

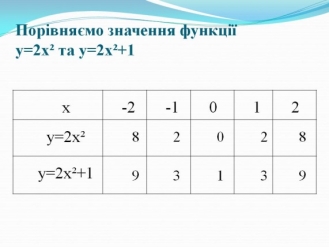
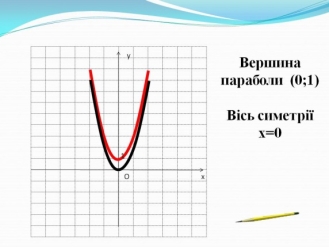
Рис. 5

2. Із графіка функції у=х² побудувати графіки функцій:
   а)  у = х²+2
   б)  у = х² - 4
   в)  у = -х²+3
   г)  у = -х² - 4

 

3. Побудуємо графіки функцій  у=2х² та у=2(х-1)²    (рис. 6).

 

  

 

   

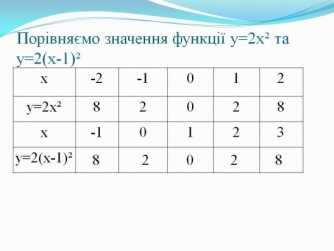
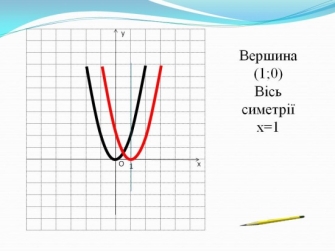
Рис. 6

4. Із графіка функції  у=х²  побудувати графіки функцій:
   а)  у = (х-3)²
   б)  у = (х+2)²
   в)  у = - (х-1)²
   г)  у = - (х+1)²

 

      

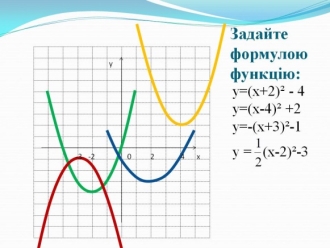
Рис. 7

 

4.               Закріплення вивченого матеріалу

 

Зібратися разом – це початок,
працювати разом – це успіх

І. Виконання  усних  вправ.    Гра «Хто краще знає та пам’ятає» (учні виконують усно, спираючись на раніше прослуханий матеріал)  (рис. 8).

 

   

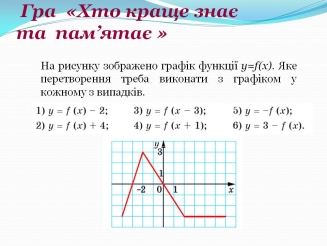
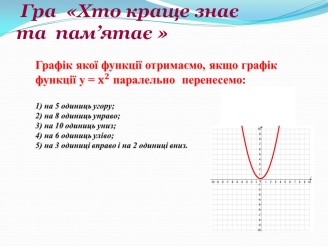
Рис. 8

 

ІІ. Гра «Упізнай мене» (учні повинні по намальованому графіку назвати  функцію)  (рис. 9).

 

  

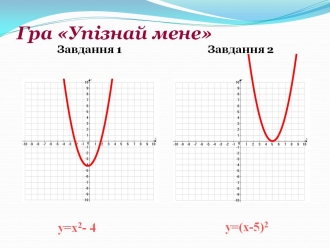
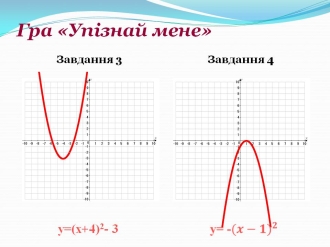
Рис. 9

ІІІ. Гра «Четвертий зайвий» (на слайді є чотири  графіки і лише три формули, що задають їх. Треба вибрати зайвий малюнок) (рис. 10).

 

  

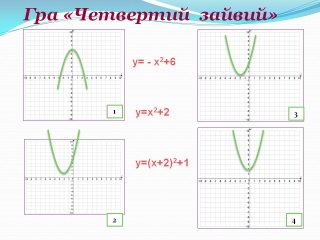
Рис. 10

 

Робота з підручником

№ 9.28 (1, 2)

Самостійна робота

 

5.               Підсумок уроку

Знайдіть відповідність  (рис. 11).

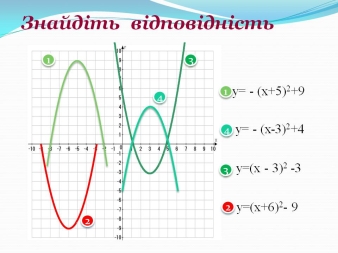
Рис. 11

 

6.               Домашнє завдання

          П. 9 ст. 81 – 89,    №№ 9.11,  9.22,  9.29