Урок "Періодичність тригонометричних функцій. Графіки тригонометричних функцій"
Розробка уроку "Періодичність тригонометричних функцій. Графіки тригонометричних функцій" із застосуванням комп'ютерної програми «Master Function»
Мета уроку "Ввести поняття періоду та періодичності. Вивчити властивості тригонометричних функцій, навчитись будувати графіки тригонометричних функцій; розвивати математичну компетентність учнів, прищеплювати навички ділового спілкування, виховувати почуття товариськості, взаємовиручки"
![]()
![]()

![]()


![]()
![]()
![]()
Тема
Періодичність тригонометричних функцій.
Графіки тригонометричних функцій
Мета
Ввести поняття періоду та періодичності. Вивчити властивості тригонометричних функцій, навчитись будувати графіки тригонометричних функцій; розвивати математичну компетентність учнів, прищеплювати навички ділового спілкування, виховувати почуття товариськості, взаємовиручки.
Тип уроку. Комбінований
Хід уроку
І. Організаційний момент
ІІ. Актуалізація опорних знань (у формі бліц – опитування)
- Що таке функція?
- Область визначення та множина значень функції?
- Парність та непарність функції, приклади;
- Зростання та спадання функції;
-
Дати означення синуса, косинуса, тангенса і котангенса будь-якого кута від
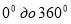 ;
;
- Що називається радіанною мірою кута, навести приклади.
ІІІ. Сприйняття й усвідомлення нового матеріалу
1. Означення. Функція ![]()
![]() називається періодичною з періодом Т
називається періодичною з періодом Т![]() 0, якщо для будь-якого х з області визначення функції числа
0, якщо для будь-якого х з області визначення функції числа ![]()
![]() та
та ![]() також належать області визначення і виконується умова:
також належать області визначення і виконується умова: ![]() .
.
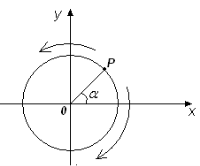 Коли точка Р , яка задає кут
Коли точка Р , яка задає кут ![]() виконає повний оберт у додатному (від'ємному) напрямку, вона займе знову початкове положення на колі і визначатиме кут
виконає повний оберт у додатному (від'ємному) напрямку, вона займе знову початкове положення на колі і визначатиме кут ![]() . Координати точки Р при такому переміщенні не зміняться, а отже, і значення всіх тригонометричних функцій залишиться без змін.
. Координати точки Р при такому переміщенні не зміняться, а отже, і значення всіх тригонометричних функцій залишиться без змін.
Кількість повних обертів може бути будь-яким цілим числом, а тому і значення тригонометричних функцій кута ![]() повторюватимуться через будь-яку кількість повних обертів в будь-якому напрямку.
повторюватимуться через будь-яку кількість повних обертів в будь-якому напрямку.
Таким чином, будь-яке число, кратне 360 є періодом всіх тригонометричних функцій, або математичною мовою, період всіх тригонометричних функцій-
![]()
![]() , або в радіанній мірі
, або в радіанній мірі ![]() . Найменшим додатним періодом функцій
. Найменшим додатним періодом функцій ![]() є число
є число ![]() . Для функцій
. Для функцій ![]() найменший додатний період
найменший додатний період ![]() .
.
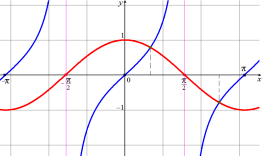
2. Графіки тригонометричних функцій
1. Графік функції ![]()
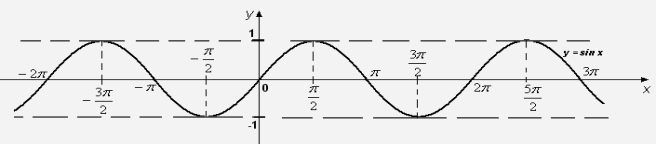
2. Графік функції ![]()

3. Графік функції ![]() 4. Графік функції
4. Графік функції ![]()
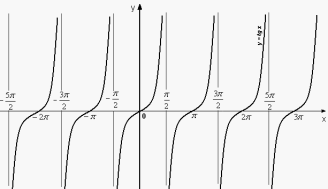
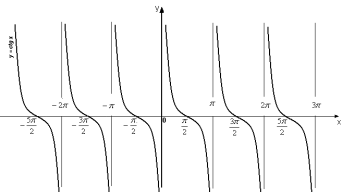
3. Властивості тригонометричних функцій (табл.)
|
№ |
Функція Влас- тивість |
|
|
|
|
|
1 |
Область визначення |
|
|
|
|
|
2 |
Множина значень |
|
|
|
|
|
3 |
Парність (непарність) |
Непарна |
Парна |
Непарна |
Парна |
|
4 |
Періодич -ність |
|
|
|
|
|
5 |
Нульові значення |
|
|
|
|
|
6 |
Проміжки зростання |
|
|
|
Не має |
|
7 |
Проміжки спадання |
|
|
Не має |
|
|
8 |
Додатні значення |
|
|
|
|
|
9 |
Від'ємні значення |
|
|
|
|
|
10 |
Найбільше значення |
|
|
Не має |
Не має |
|
11 |
Найменше значення |
|
|
Не має |
Не має |
-
Приклад 1. Побудувати графік функції
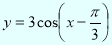
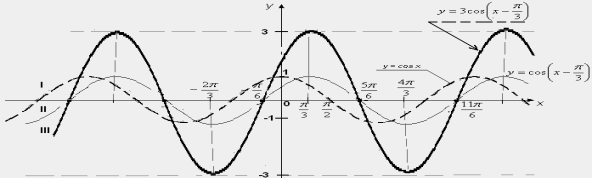
Розв'язання І. Побудуємо графік функції ![]() .
.
ІІ. Графік функції ![]() отримуємо перенесенням графіка функції
отримуємо перенесенням графіка функції ![]() в додатному напрямі вздовж осі Ох на відстань
в додатному напрямі вздовж осі Ох на відстань ![]() .
.
ІІІ. Графік функції ![]() отримуємо розтягуванням в 3 рази графіка функції
отримуємо розтягуванням в 3 рази графіка функції ![]() вздовж осі Оу
вздовж осі Оу
-
Приклад 2. Побудувати графік функції
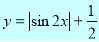
І. Побудуємо графік функції ![]() ;
;
ІІ. Стиснувши графік функції ![]() вздовж осі Ох вдвічі отримаємо графік функції
вздовж осі Ох вдвічі отримаємо графік функції ![]() ;
;
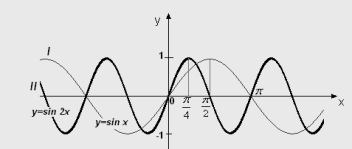
ІІІ. Щоб отримати графік функції ![]() , відображаємо ту частину графіка ІІ, для якої
, відображаємо ту частину графіка ІІ, для якої ![]()
(нижче осі Ох) симетрично відносно осі Ох.
IV. Графік функції ![]() отримаємо, перемістивши графік ІІІ, вгору вздовж осі Оу на
отримаємо, перемістивши графік ІІІ, вгору вздовж осі Оу на ![]()
-
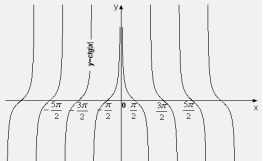 Приклад 3. Побудувати графік функції
Приклад 3. Побудувати графік функції 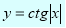
І. Так як ![]() при
при![]() , то спочатку можна
, то спочатку можна
побудувати графік функції ![]() , для
, для ![]() .
.
ІІ. Функція ![]() є парною, отже інша частина
є парною, отже інша частина
графіка (при ![]() ) – симетрична побудованій
) – симетрична побудованій
відносно осі Оу.
ІV. Побудова графіків та вивчення властивостей тригонометричних функцій
за допомогою комп’ютерної програми «Master Function»
1. 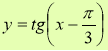 2.
2. ![]()
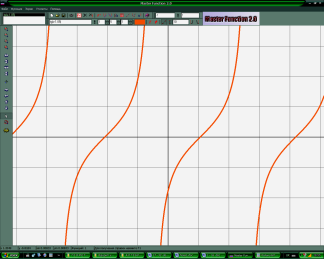
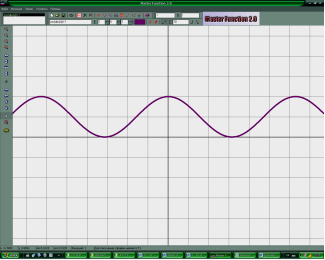
3. ![]() 4.
4. ![]()
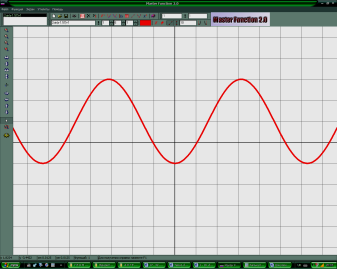
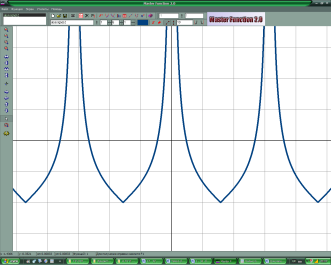
V. Підсумок уроку. Домашнє завдання: стор 17 – 20 , § 20; вправа 3 (б, д, е)
1

про публікацію авторської розробки
Додати розробку
