Урок "ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ І ПЛОЩИН У ПРОСТОРІ".

Конспект уроку:

ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ

І ПЛОЩИН У ПРОСТОРІ.

10 КЛАС

Підготувала:

Шкатула Лариса Павлівна

вчитель математики

КЗ "Балашівська гімназія

Міської ради міста

Кропивницького"

м. Кропивницький

2021

Тема: ПЕРПЕНДИКУЛЯРНІСТЬ ПРЯМИХ І ПЛОЩИН У ПРОСТОРІ.

Тип: узагальнення і систематизація знань.

Мета:

навчальна: узагальнення і систематизація знань з теми, закріплення вмінь і навичок розв’язання задач на перпендикулярність прямих і площин у просторі;

розвивальна: розвиток логічного мислення та просторової уяви, вміння аналізувати та робити висновки;

виховна: виховання графічної культури, уважності, акуратності, дисциплінованості, поваги до думки товариша;  акцентувати  увагу  учнів  на  зв'язок  предмету  з  життям, практичним  застосуванням  отриманих  з  теми  знань.

Методи проведення: робота в малих групах, бесіда, фронтальне опитування, демонстрація,  .

Унаочнення: презентація, таблиці, картки із завданнями, моделі до задач.

Обладнання: проектор, екран, комп’ютер, лінійки, олівці.

Попередньо клас розбивається на 4 групи. Ці групи можуть комплектуватися за принципом вільного взаємного вибору учнів або ж за вибором вчителя. Кожній з них напередодні дається по 5 задач (по одній задачі кожного типу). Учні готують розв’язання і просторові моделі до цих задач (з картону, дерева, металу, проволоки тощо).

ЗМІСТ І ХІД ЗАНЯТТЯ.

 І. Організаційна частина . Перевірка присутності учнів, підготовленості аудиторії до заняття.

ІІ. Перевірка домашнього завдання. Наявність домашньої роботи у зошитах, перевірка правильності розв’язання шляхом усного коментування відповідей.

 ІІІ. Актуалізація опорних знань.

1. Формули радіусів вписаного і описаного кола трикутників (рівностороннього, різностороннього, прямокутного).

2. Де знаходяться центри вписаного і описаного кіл трикутника?

 3. Теорема синусів, її наслідок.

 4. Теорема косинусів.

 5. Теорема Піфагора. Співвідношення між сторонами і кутами прямокутного трикутника.

6. Формули для обчислення площі трикутника.

ІV. Мотивація навчання.

Шановні учні, ми закінчуємо  вивчати тему „Перпендикулярність прямих і площин  у просторі”. Впевнилися, що нас оточують предмети, в яких можна побачити перпендикулярність прямих (плінтуси підлоги, перекладина та підпорки спортивного снаряду і т.д.), перпендикулярність прямої і площини (стовп і поверхня землі, підлога і ніжка стола чи стільця і т.д.), перпендикулярність площин (стіна і стеля, стінки шафи і т.д.).

Ми вивчили означення перпендикулярності, сформулювали і довели ознаки, за якими визначається перпендикулярність. Тож на сьогоднішньому уроці ми повинні узагальнити та систематизувати свої знання з даної теми, провести корекцію вмінь і навичок застосовувати вивчені ознаки і теореми до розв’язування задач.

Оголошення теми і мети заняття.

V. Узагальнення і систематизація теоретичного матеріалу.

Перед тим, як перейти до практичного застосування набутих знань, давайте з вами повторимо теоретичний матеріал з даної теми.  Для цього пропоную разом розгадати кросворд та пройти індивідуально тестування .

         Кросворд

1. Відрізок, який сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини, називається…(перпендикуляр)

2. З двох похилих більша та, проекція якої …(більша)

3. Якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до її… (проекції)

4. Якщо кут між площинами дорівнює 90⁰, то площини називаються …(перпендикулярними)

5. Перпендикуляр…за будь-яку похилу (менший).

6. Фігура, утворена двома півплощинами і  спільною прямою, що їх обмежує називається … кутом (двогранним)

7. Скільки прямих, перпендикулярних площині, можна провести через точку, що не належить даній площині (одну).

8. Відрізок, що з’єднує основи перпендикуляра і похилої називається …(проекцією).

9. Якщо площина перпендикулярна до однієї з двох…прямих, то вона перпендикулярна і до другої (паралельних).

10. Якщо напрямок проектування - деяка  пряма l перпендикулярна до площини проекцій , то таке проектування називають…(ортогональним)

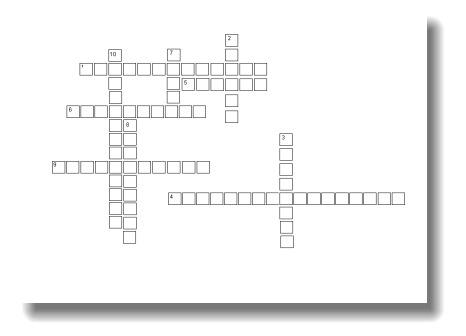
На розгадування кросворду відводиться  не більше 5 хв. Після завершення роботи  кожна група по черзі називає свою відповідь на питання, після чого правильна відповідь  виводиться  на екран.

Тестування (пропоную учням перейти за посиланням  і виконати тестову роботу на освітній платформі "На Урок", https://naurok.com.ua/test/join?gamecode=1026993)

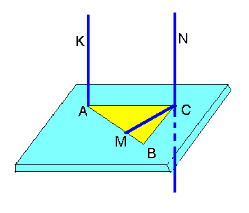
1. Яким є взаємне розміщення прямих AK i  NC,

 якщо АК ┴ (АВС)   і NC ┴ (АВС)?

      а) паралельні;          б) мимобіжні; 

    в) перпендикулярні;     г) перетинаються.

2. У просторі дано пряму а і точку А поза нею, скільки існує прямих, що є перпендикулярними до прямої а і проходять через точку А?

     а) визначити неможливо;  б) одна;   в) нескінченна множина;   г) жодної.

3. Скільки площин, перпендикулярних до даної прямої можна провести через точку, що лежить на даній прямій?

      а) нескінченну множину;   б) тільки одну;    в) тільки дві;      г) жодної.

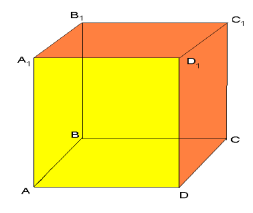
4. Використовуючи малюнок, вкажіть пряму, що перпендикулярна до прямої СС₁ і проходить через точку А.

         а) СВ;        б) АС;        в) CD;       г) А₁С₁

5. Використовуючи малюнок, вкажіть пряму, яка перпендикулярна до площини АВВ₁.

         а) BD;         б) ВС;       в) АВ;        г) АС

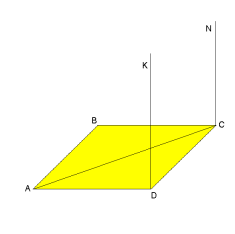
6. Яким є взаємне розміщення прямої  KD  і площини АВС, якщо KD ║NC i NC ┴ (ABC)?

а) паралельні;    б) визначити неможливо;

в) не перетинаються;     г)перпендикулярні

7. Якщо одна з двох паралельних  прямих перпендикулярна до третьої прямої, то

а)  друга пряма завжди паралельна третій прямій;

б) друга пряма завжди мимобіжна з третьою прямою;

в)  друга пряма ніколи не перетинає третю пряму;

г) і друга пряма перпендикулярна до третьої прямої

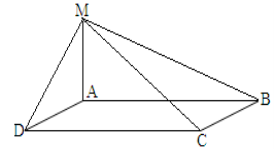
8. Відрізок АМ проведено перпендикулярно до площини  

 прямокутника   АВСD.

Який відрізок   має більшу довжину?

   а) МА;      б) МD;   в) МВ;      г) МС;        д) АD.

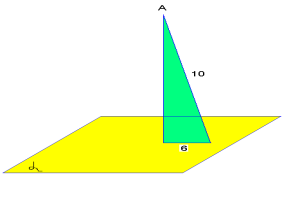9. З точки А до площини 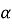проведено похилу завдовжки 10 см.

Знайдіть відстань від точки А до площини,

якщо проекція похилої на площину дорівнює 6 см.

          а) 4 см;        б) 8 см;        в) 64 см;       г) 2 см. 

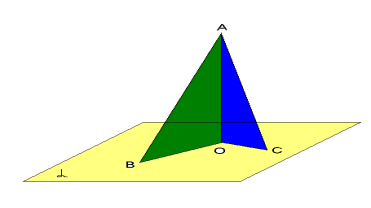10.  З точки А до площини проведено дві похилі АВ і АС і перпендикуляр АО. Відомо, що АВ >АС. Виберіть правильне твердження.

а) АВ < AO;    б) CO > OB;      в) AC < AO;      г) CO < OB

VІ. Розв’язування задач.

Переходимо, безпосередньо, до практичного застосування набутих теоретичних знань.    Весь комплекс задач теми було розбито на п’ять типів:

1.  Задачі на доведення. 

• Точка М знаходиться на однаковій відстані від сторін кута АВС і не належить його площині. Доведіть, що її ортогональна проекція на площину кута належить бісектрисі цього кута, якщо вона знаходиться у внутрішній області цього кута. 

• Доведіть, що коли дві площини   і  перпендикулярні до прямої а, то вони паралельні.

• Перпендикулярні площини  і  перетинаються по прямій а .

В площині   проведена пряма, перпендикулярна прямій а. Доведіть, що ця пряма перпендикулярна і до площини . 

• Три площини попарно перпендикулярні. Доведіть, що прямі їх перетину також попарно перпендикулярні.

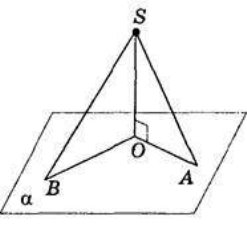2. Похилі та їх проекції

• Із даної точки до площини проведено дві похилі, різниця довжин яких 6см. Їх проекції на цю площину дорівнюють 27см і 15см. Знайдіть відстань від даної точки до площини. 
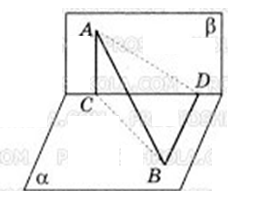• Із точки, що знаходиться на відстані 12см від площини, проведено до цієї площини дві похилі, довжини яких 13см і 20см. Відстань між основами похилих дорівнює 19см. Знайдіть кут між проекціями цих похилих. 
• Відрізок довжиною 25см опирається кінцями на дві взаємоперпендикулярні площини. Відстані від кінців відрізка до площин дорівнюють 15см і 16см. Знайдіть проекції відрізка на кожну із площин. 
• Через одну сторону ромба проведено площину на відстані 4м від протилежної сторони. Проекції діагоналей на цю площину дорівнюють 8м і 2м. Знайдіть проекції сторін.

3.  Задана точка рівновіддалена від вершин трикутника або чотирикутника. 

• АВС – правильний трикутник, точка О – його центр. ОК – перпендикуляр до площини цього трикутника. ОК=1см. Сторона трикутника дорівнює 3см. Знайдіть відстані від точки К до вершин трикутника. 
• Основа і висота рівнобедреного трикутника дорівнюють по 4см. Дана точка знаходиться на відстані 6см від площини трикутника і на однаковій відстані від його вершин. Знайдіть цю відстань.
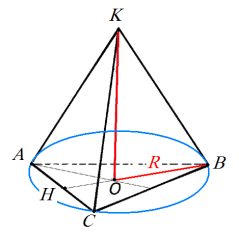
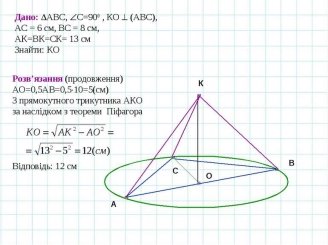
• Катети  прямокутного трикутника дорівнюють 6 см і 8 см. Поза площиною цього трикутника дано точку, яка знаходиться на відстані 13 см від кожної його вершини. Знайдіть відстань від цієї точки до площини трикутника. 
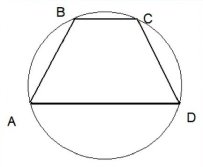• Трапеція вписана в коло, причому менша її основа, що дорівнює 16см,  стягує дугу 60 ⁰ . На відстані 12см від площини трапеції знаходиться точка, рівновіддалена від усіх вершин трапеції. Знайдіть відстань від точки до вершин трапеції.

4. Задана точка рівновіддалена від сторін трикутника або чотирикутника. 

• Катети  прямокутного   трикутника дорівнюють 12см і 16 см.  Точка, рівновіддалена від усіх сторін трикутника, розміщена  на відстані  3 см від площини трикутника. Знайдіть відстані від дано точки  до сторін трикутника.

• Дано трикутник із сторонами 26см, 28см і 30см. Точка Р віддалена від усіх сторін трикутника на 17см. Знайдіть відстань від точки Р до площини трикутника. 

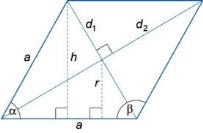
• Діагоналі ромба дорівнюють 12см і 16см. Точка К знаходиться поза площиною ромба і віддалена від усіх сторін ромба на 8см. Знайдіть відстань від точки К до площини ромба. 

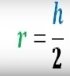
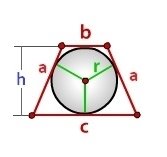• Рівнобічна трапеція, периметр якої 48 см, а гострий кут 60 ⁰ , лежить у площині α . Точка, рівновіддалена від усіх сторін трапеції, знаходиться на відстані 3см від площини α. Знайдіть відстань від цієї точки до сторін  трапеції.                       

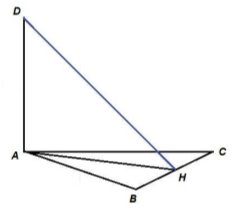5. Задана точка проектується у вершину або на сторону трикутника чи чотирикутника. 

• У трикутнику АВС сторона АВ=15см, АС=13см, СВ=14см. Із вершини А проведено до його площини перпендикуляр, який дорівнює 16см. Знайдіть відстань від його кінця до сторони ВС. 

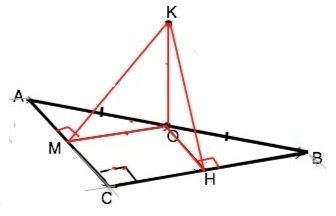
• Катети прямокутного трикутника дорівнюють 18см і 32см. До площини  трикутника із середини гіпотенузи проведено перпендикуляр, який дорівнює 12см. Знайдіть відстань від кінця перпендикуляра до катетів. 

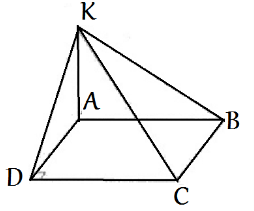
• До площини прямокутника АВСD через його вершину А проведено перпендикуляр АК, кінець якого К віддалений від сторони ДС на 2,4 см, від сторони ВС – на 2,8см, від вершини С – на 3,6см. Знайдіть АК.

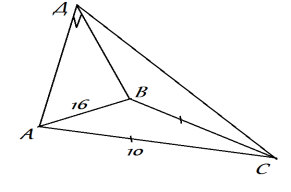• Рівнобедрені трикутники АВС і АВD мають спільну сторону АВ і лежать у перпендикулярних площинах. Знайдіть відстань СD, якщо АВ=16 см,  АDВ=90 ⁰, АС=ВС=10см.

 Кожна група готує по одній задачі кожного типу. Потім по представнику з групи (за вибором учителя), демонструючи виготовлену попередньо модель, розв’язують задачу біля дошки. Решта учнів роблять відповідні записи та виконують малюнки у зошитах, задають питання.

Після розв’язання задачі кожному із учнів ставиться завдання для усного розв’язання.

Чи правильні у стереометрії такі твердження? 

•                 Через точку, яка лежить на даній прямій, можна провести тільки одну пряму, перпендикулярну до цієї прямої. 
•                 Прямі, перпендикулярні до однієї і тієї самої прямої, паралельні між собою.
•                 Якщо пряма проходить через точку кола перпендикулярно до радіуса,  проведеного до цієї точки, то вона є дотичною до кола. 
•                 Якщо площина перпендикулярна до даної площини, то вона перпендикулярна і до довільної прямої, паралельної цій площині. 
•                 Якщо площина і пряма перпендикулярні до однієї й тієї самої площини, то вони паралельні між собою.

IV. Узагальнення і систематизація набутих знань та вмінь.

Для кожної  групи  - однакова задача.

Ваше завдання - якомога швидше розв’язати її.

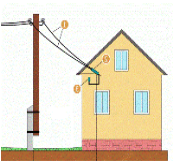
Задача. Потрібно протягнути два електричні дроти від стовпа до будинку. На стовпі вони кріпляться на висоті 19 м, а на стіні будинку - 9 м. Скільки потрібно дроту, якщо відстань від стовпа до будинку становить 30 м, а на кріплення і провисання слід додати 5% знайденої довжини.

Розв'язання

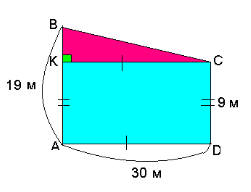
Стовп перпендикулярний площині Землі і стіна будинку перпендикулярна площині Землі, отже, оскільки дві прямі, перпендикулярні одній і тій самій площині, паралельні між собою, з цього випливає, що математична модель задачі - прямокутна трапеція.

Отже, АВ = 19 м, CD = 9 м, AD = 30 м.  Знайдемо ВС.

Опустимо перпендикуляр СК на сторону АВ.  АК = CD = 9 м, отже,

ВК = АВ - АК = 19 - 9 = 10 (м).        К С = AD = 30 м.

З Δ ВСК ():

ВС =   = = (м)

1) 10∙2 = 20 (м) - довжина 2-х дротів.

2) 20∙0,05 = (м) - на провисання.

3) 20 = 21 (м)

Відповідь: необхідно 21 м дроту.

 VІ. Підведення підсумків заняття.

Таким чином, сьогодні повторили теоретичний матеріал та розглянули основні принципи розв’язання задач з теми „ Перпендикулярність у просторі”.

Я думаю, що після цього заняття ви добре засвоїли матеріал і готові до тематичного оцінювання.

VІІ. Оцінювання роботи учнів. Оголошення домашнього завдання.