КЗО «Циганівська ЗШ І-ІІІ ступенів»

 

 

 

 

 

 

 

 

 

 

"Піраміда.

Правильна піраміда.

Бічна і повна поверхня піраміди."

 

 

 

 

 

 

 

 

 

 

 

З досвіду роботи

вчителя математики

СІМОНЧИКОВОЇ

ЛЮДМИЛИ   ГРИГОРІВНИ, спеціаліста

вищої кваліфікаційної категорії

 

 

 

 

 

 

 

с. Циганівка

 

Тема : Піраміда. Правильна піраміда. Бічна і повна поверхня піраміди.

Мета :

• Дати означення піраміди, правильної піраміди, довести властивості пірамід, ввести поняття бічної і повної поверхонь піраміди, вивести формулу для обчислення  бічної  поверхні піраміди і повної поверхні піраміди, у якої двогранні кути при основі рівні;
• розвивати логічне мислення учнів шляхом постановки проблемних запитань, розвивати просторову уяву учнів;
• виховувати організованість і дисципліну розумової праці учнів.

Тип уроку : Урок засвоєння нових знань.

Обладнання : Моделі пірамід,  таблиці із стереометрії для 11 класу.

 

Хід уроку.

 

І. Організаційний початок уроку.

 

ІІ. Повідомлення теми, мети і завдань уроку.

    Вступна розповідь з використанням моделей пірамід, історична довідка про піраміди.

 

ІІІ. Засвоєння нових знань.

    Виклад нового матеріалу здійснюється у формі лекції з елементами евристичної бесіди.

План лекції :

1.      Піраміда та її  елементи.

2.      Властивості піраміди.

3.      Правильна піраміда та її властивості.

4.      Бічна поверхня і повна поверхня піраміди.

 

1.     Піраміда, елементи піраміди.   

      Означення – 1 Пірамідою називається многогранник, у якого одна грань – основа піраміди -  довільний многокутник, а інші бічні грані – трикутники зі спільною вершиною, яка називається вершиною піраміди.

 

 

SABCDЕ – піраміда,

т. S – вершина піраміди.

ABCDЕ – основа піраміди.

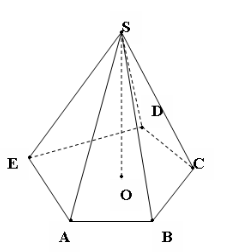
Трикутники SЕA,  SAB, SBC, SDC, SDЕ –

бічні грані піраміди,

SЕ,  SA, SB, SC, SD – бічні ребра піраміди.

 

      Означення – 2   Перпендикуляр, опущений з вершини піраміди на площину основи, називається висотою піраміди.

 SО  ┴   пл.ABCDЕ; SО – висота піраміди, SО = H (позначення висоти).

    Залежно від виду многокутника, що лежить в основі піраміди, пірамди поділяються на трикутні, чотирикутні, п’ятикутні, …, n – кутні.

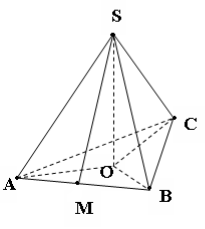
    Задача 1  ( Завдання за готовим кодопозитивом ) 

 

 

 SABC – трикутна піраміда;

 SО – висота піраміди;

 Назвати :

1)     проекції бічних ребер на пл. основи;

2)     кути нахилу бічних ребер до площини основи.

 

 

 

 

 2. Властивості піраміди.    

      Твердження 1 Якщо для піраміди виконується одна з умов :

• усі бічні ребра піраміди рівні;
• усі бічні ребра утворюють з площиною основи рівні кути;
• кути між бічними ребрами і висотою піраміди рівні,

то вершина піраміди проектується в центр кола, описаного навколо піраміди, а бічні ребра – в радіус цього кола.

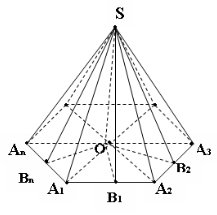
Дано:  SА₁А₂А_3…Аn – n –кутна піраміда.

SО – висота піраміди, т.О – основа висоти;

SА_1, SА_2,  SА_3…SАn – бічні ребра піраміди,

ОА_1, ОА_2, ОА_3…ОАn – їх проекції на пл. основи,

ےSА₁О,    ےSА₂О, …   ےSАnО – кути нахилу бічних ребер до площини основи.

SА₁ = SА₂ = _…= SАn  або

   ےSА₁О =    ےSА₂О = …  ے SАnО  або

  ے А₁SО =   ے А₂SО = … ے  АnSО 

Довести : т.О – центр кола, описаного навколо основи піраміди.

Доведення.

    (Пригадаємо,  де  лежить  центр  кола,  описаного навколо  многокутника;  наголосити, що т.О –  точка перетину серединних перпендикулярів до сторін основи піраміди).

    Розглянемо спочатку виконання першої умови.

Якщо SА₁ = SА₂ = _…= SАn ,  то   SО А₁=    SОА₂=…=    SОАn  ( за гіпотенузою та катетом, SО – спільний катет).

    З рівності цих прямокутних трикутників, випливає, що ОА₁= ОА₂=…= ОАn, тобто т.О –рівновіддалена від вершин  А_1, А_2, А_{3 …} Аn основи піраміди, а отже, є центром кола, описаного навколо основи піраміди, і   ОА₁= ОА₂=…= ОАn = R – радіуси цього кола.

    Для випадку виконання інших двох умов учні здійснюють доведення самостійно, як вправу для домашнього завдання.

      Завдання 2 Назвати кути нахилу бічних граней до площини основи.

 (Використовую таблиці стереометрії №14)

      Завдання 3 Побудувати кут нахилу грані  SА₁А₂  до площини основи піраміди.

 (Використовую готовий малюнок №3)

    Побудова. У грані SА₁А₂  проведемо з вершини S перпендикуляр SВ₁ до А₁А_{2 ,} тоді точку  В₁ сполучаємо з т.О,   ОВ₁   ┴      А₁А₂  ( за теоремою про три перпендикуляри ). 

SО   ┴     площині А₁А₂А_3…Аn .

    Отже, кут SВ₁О – лінійний кут двогранного кута з ребрами А₁А_2, тобто кут нахилу грані SА₁А₂  до площини основи. Аналогічно будуються інші кути.

      Твердження –2 Якщо для піраміди виконується одна з трьох умов :

• усі бічні грані утворюють з основою рівні кути;
• довжини висот усіх бічних граней рівні;
• висоти бічних граней утворюють з висотою піраміди рівні кути,

тоді вершина піраміди проектується в центр кола, вписаного в основу піраміди. 

Виконати малюнок до задачі.

 

Дано:  SА₁А₂А_3…Аn – n –кутна піраміда.

SО – висота піраміди, т.О – основа висоти;

SВ_1, SВ_2,  SВ_3…SВn – висоти бічних граней,

  ے SВ₁О,   ے SВ₂О, … ے  SВnО – кути нахилу бічних граней до площини основи.

  ے В₁SО,  ے  В₂SО, …  ے ВnSО – кути між висотами бічних граней і висотою піраміди.      

  ے SВ₁О =   ے SВ₂О = … =  ے SВnО або

SВ₁ = SВ₂ = _…= SВn  або

 ے  В₁SО =   ے В₂SО = …  ے ВnSО

    Довести : т.О -   центр кола, вписаного в основу піраміди.

( Пригадаємо де лежить центр кола, вписаного в многокутник; наголосити , що т.О – точка перетину бісектрис кутів в основі піраміди ).

    Нехай  ے SВ₁О =   ے SВ₂О = … =  ے SВnО .

ОВ_1, ОВ_{2 …}ОВn – проекції висот  SВ_1, SВ_{2 …} SВn на площину основи.

ОВ₁   ┴      А₁А_2;  ОВ₂    ┴     А₂А_{3 ;…} ОВn   ┴     А₁Аn  ( за теоремою про три перпендикуляри ),  отже,  ОВ_1, ОВ_{2 …}ОВn – відстані від т.О до сторін  А₁А_2;  А₂А_{3 ;…} А₁Аn відповідно.

Трикутники   SОВ₁, SОВ₂, … SОВn – прямокутні.

     SОВ₁ =      SОВ₂ = … =      SОВn  (бо SО – спільний катет, а  ے SВ₁О =    ےSВ₂О = … =   ےSВnО за умовою).

    З рівності цих трикутників випливає, що  ОВ₁ = ОВ₂ = … = ОВn, тобто т.О – рівновіддалена від сторін основи, а отже, є центром кола, вписаного в основу піраміди.

    ЗАДАЧА Бічне ребро піраміди утворює рівні кути із суміжними сторонами основи. Довести, що основа висоти піраміди лежить на бісектрисі кута, утвореного цими сторонами основи.  

 

 

Дано :  SABC – трикутна піраміда,

               SО – висота піраміди,

             SА -  бічне ребро,

                ےSАС =  ے SАВ

Довести : т.О – належить бісектрисі  ے ВАС. 

 

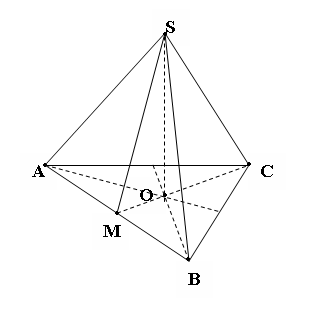
Доведення:

    1) Проведемо SМ  ┴  АВ в грані  SАВ і  SN  ┴  АС в грані SАС.

    2)    SNА і   SМА – прямокутні й рівні ( SА – спільна гіпотенуза,   ے SАN =   ے SАМ за умовою), отже SN = SМ.

    3) Сполучимо т.О – з точками N і М. ОN – проекція SN на пл. основи; 

ОМ – проекція SМ на пл. основи, отже ОN  ┴    АС; ОМ  ┴    АВ (за теоремою про три перпендикуляри), ОN = ОМ, бо SN = SМ ( за доведеним ).

4)     Отже, т.О рівновіддалена від сторін кута ВАС, тобто лежить на бісектрисі цього кута.

    Доведений факт справедливий і у випадку  n –кутної  піраміди, тому робимо такий висновок.

      Твердження – 3  Якщо бічне ребро піраміди утворює рівні кути із суміжними сторонами основи, то основа висоти піраміди лежить на бісектрисі кута, утвореного цими сторонами основи.

3.     Правильна піраміда і її властивості. 

      Означення – 3  Піраміда називається правильною, якщо в її основі лежить правильний многокутник і основа висоти збігається з центром цього многокутника.

      Означення – 4  Висота бічної грані правильної піраміди, проведена з вершини піраміди, називається апофемою піраміди.

      Означення – 5   Віссю правильної піраміди називається пряма, яка містить її висоту.   

    За готовими таблицями ( таблиці №10, №11 ) робимо аналіз побудови правильної піраміди, наголошую на правильності побудови правильного многокутника. пригадуємо, де лежить центр у правильному трикутнику, чотирикутнику, шестикутнику, повторюємо властивості медіан у трикутнику. Пояснюю побудову правильної  шестикутної піраміди.

 Властивості правильної піраміди :

 1) Бічні ребра правильної піраміди рівні і утворюють з площиною основи рівні кути.

 2) Усі бічні грані правильної піраміди – рівні рівнобедрені трикутники.

 3) Плоскі кути при вершині піраміди рівні.

 4) Апофеми піраміди рівні.

 5) Двогранні кути при сторонах основи рівні.

 6) Двогранні кути при бічних ребрах рівні.

    Для самостійного доведення : властивості 1-4. У класі довести 5 і 6 властивості.

      4. Бічна і повна поверхні піраміди.   

      Означення - 6  Бічною поверхнею називається сума площ її бічних граней.

    Задача (самостійно) Сторона основи правильної  n–кутної  піраміди дорівнює а, апофема l

Знайти площу бічної поверхні піраміди.

Розв’язання.

     S_б = ¹/₂  (а  l )n,  де n – кількість бічних граней,

     S_б = ¹/₂     (а n) l = ¹/₂     Р l , оскільки  Р =  а n, отже,

 

 

Sб = ½  P l

 

де    - l апофема,  Р – периметр основи.

 

    Теорема.  Бічна поверхня піраміди  дорівнює добутку півпериметра основи на апофему.

                      S_б = ¹/₂  Р l

      Означення 7  Повною поверхнею піраміди називається сума її бічної поверхні та площі основи.

 

 

 

 

 

 

    Запитання до учнів : Сформулювати властивість площі ортогональної проекції многокутника.

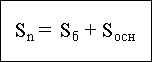    Задача 3 Знайти бічну поверхню піраміди, у якої площа основи Q   ,а двогранні кути при основі дорівнюють     .

 

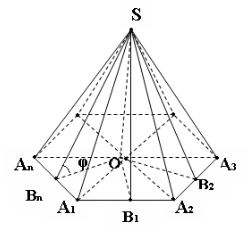
Дано : МА₁А_2…Аn – n –кутна піраміда.

            МО – висота піраміди,

            А₁А_2…Аn – основа. 

            S_А1А2…Аn  =  Q

               ے МВ₁О =    ےМВ₂О = … =   ےМВnО = φ

Знайти :  S_б   

 

 

Розв’язання.

S Δ A1A2M = S Δ A1A2O / cos φ ,

S Δ A2A3M = S Δ A2A3O / cos φ , …

S ΔA1AnM = S ΔA1AnO / cos φ , 

 

  Додавши почленно ці рівності, дістанемо :

 

S ΔA1A2M + S Δ A2A3M +… S ΔA1AnM = ΔA1A2O / cos φ + S Δ A2A3O / cos φ +… + S ΔA1AnO / cos φ= = 1/ cosφ (S Δ A1A2O + S Δ A2A3O +…+ S ΔA1AnO ) = 1/ cosφ *Q = Q / cosφ

 

 

 

 

 

Сума площ трикутників   А₁А₂О, А₂А₃О, і т.д. дорівнює площі основи, оскільки т.О – центр кола, вписаного в основу піраміди МА₁А_2…Аn .

    Отже отримаємо таке твердження :

      Твердження 4   Якщо всі грані піраміди нахилені до площини основи під однаковим кутом      , то площа бічної поверхні обчислюється за формулою

 

 

 

 

 

 

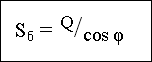
 де, Q – площа основи піраміди, φ – двогранний кут при основі.

 

5. Об’єм піраміди.

Теорема Об’єм будь-якої піраміди дорівнює третині добутку площі її основи на висоту, тобто

 

 

 

 

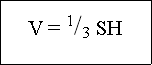
де S – площа основи піраміди, H – її висота

         Доведення теореми про об’єм піраміди проводжу у відповідності до п 69, 70 підручника

 

ІV. Узагальнення та систематизація знань.

    Для узагальнення та систематизації знань використовую усні вправи :

1. Бічні ребра піраміди рівні. Чи буде піраміда правильною? У яку точку проектується її вершина?
2. Чи може вершина трикутної піраміди, усі бічні ребра якої рівні проектуватися в точку поза її основою?
3. Чи можуть в основі правильної піраміди лежати

• рівнобедрений трикутник, 
• ромб,
• квадрат,
• трапеція.

4.      Чи можуть бічні ребра піраміди бути рівними, якщо в основі лежить :

         прямокутник,

         ромб,

         трапеція,

         паралелограм,

         многокутник,

         чотирикутник ABCD , у якого AB = BC та AD =  CD ?

5.      Усі ребра n –кутної  піраміди рівні між собою. Доведіть, що ця піраміда правильна.

6. Чи буде правильною піраміда в основі якої лежить квадрат, а ортогональною проекцією її вершини є одна з вершин квадрата?
7. Скільки потрібно мати даних, щоб визначити повну поверхню правильної n –кутної піраміди?
8. Дано піраміду, основа якої – прямокутник, а висота проходить через точку перетину діагоналей основи. Які з властивостей цієї піраміди такі самі, як у правильної? Які властивості відмінні від властивостей правильної піраміди?
9. Площа бічної поверхні правильної піраміди у два рази більша за площу основи. Під яким кутом нахилені бічні грані до площини основи?

 

V. Підсумок уроку.

   Ознайомилися  з пірамідою, її властивостями, з правильною пірамідою та її властивостями, з бічною та повною поверхнями піраміди.

 

VІ. Домашнє завдання.  

    Вивчити конспект лекції, довести відповідні твердження. Довести справедливість твердження 1,2 у випадку виконання умов 2 або 3.