Презентація "Об’єм тіла. Об’єм многогранника та властивості об’єму"
Про матеріал
Тема: "Об'єм тіла. Об'єм многогранника та властивості об'єму"
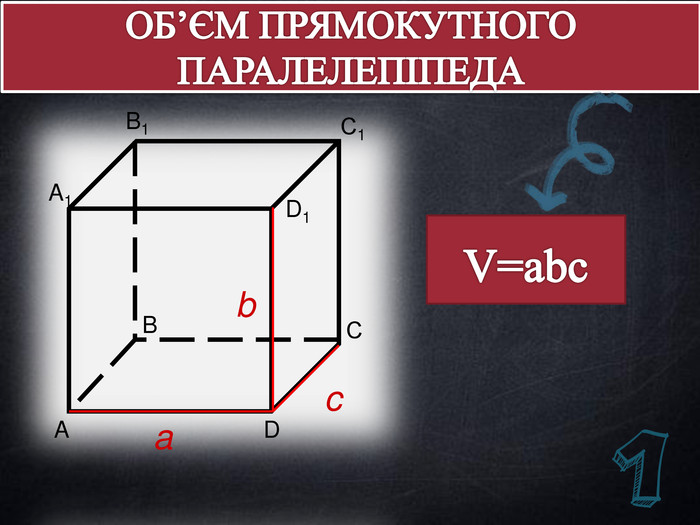
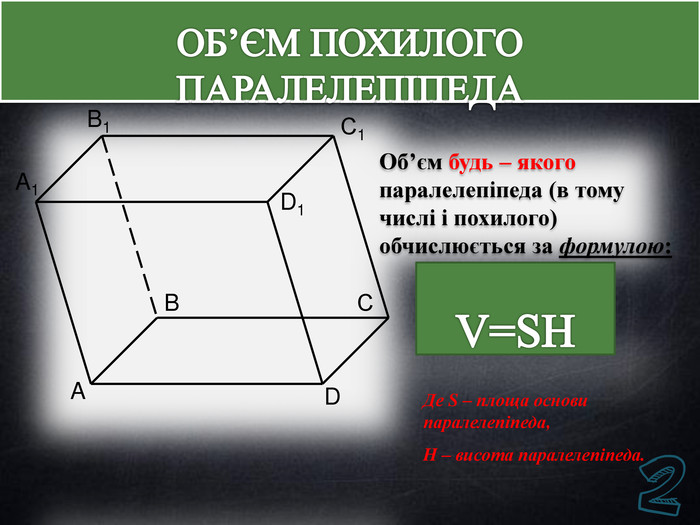
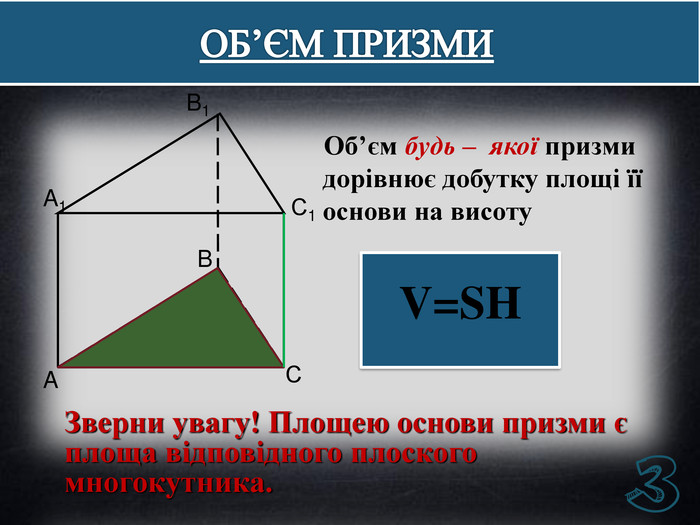
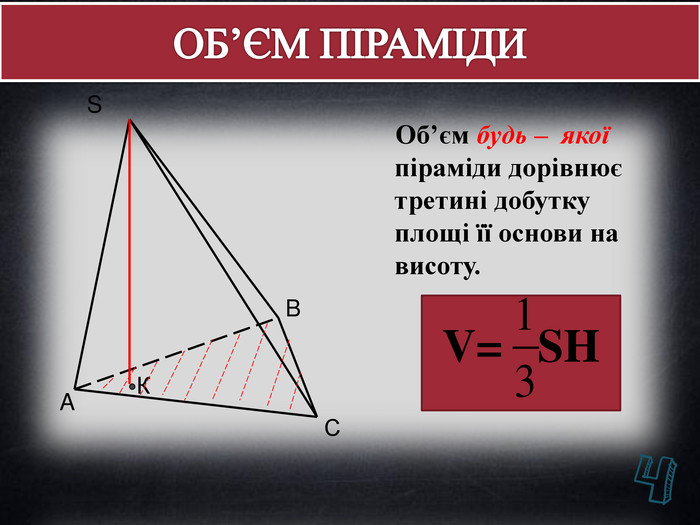
Дана презентація містить основні означення, властивості, графічні зображення, формули об'ємів многогранників, задачі на знаходження об'єму та тестові завдання для перевірки знань учнів.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


































-

Kлачик Альона Ярославівна
14.12.2024 в 12:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Єременко Наталія Олексіївна
15.01.2024 в 22:31
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жижченко Інна Яківна
10.04.2023 в 08:46
Дякую за роботу
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Іванов Сергій
22.12.2022 в 14:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Грищенко Сергій Георгійович
06.12.2021 в 15:01
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Букарева Анастасія Анатоліївна
15.01.2021 в 09:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Покудіна Лариса Степанівна
12.01.2021 в 22:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 4 відгука