Урок: Подібність трикутників. Перша ознака подібності трикутників.
Подібні трикутники. Перша ознака подібності трикутників
Конспект уроку з геометрії
для 8 класу підготувала
вчитель математики
Сантар Т.В.
Тема уроку: Подібні трикутники. Перша ознака подібності трикутників
Мета уроку:
- навчальна - сформувати в учнів уявлення про подібні трикутники; працювати над засвоєнням учнями означення подібних трикутників, змісту поняття коефіцієнта подібності; ознайомити учнів із першою ознакою подібності трикутників;
- розвивальна - розвивати логічне мислення і вміння аналізувати та узагальнювати;
- виховна - виховувати дисциплінованість та свідоме ставлення до вивчення геометрії, повагу до думки інших.
Тип уроку: засвоєння нових знань.
Наочність та обладнання: презентація «Подібні трикутники», конспект «Подібні трикутники. Перша ознака подібних трикутників», приладдя.
Хід уроку
І. Організаційний етап
ІІ. Формулювання мети і завдань уроку
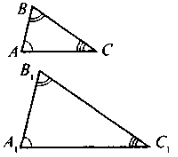
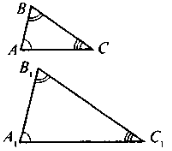
Для розуміння учнями вивчення матеріалу уроку потрібно розглянути фігури, зображені на рисунку та дати відповіді на наступні запитання:
- Які геометричні фігури зображені на цьому рисунку?
- Які саме елементи цих трикутників відповідно рівні? Чому ви так вважаєте?


![]()



ІІІ. Актуалізація опорних знань
Виконання усних вправ ( Робота за готовими малюнками)
-
Відомо, що
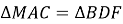 . Запишіть рівності, що з цього випливають:
. Запишіть рівності, що з цього випливають:  .
.
- Яким—гострокутним, прямокутним чи тупокутним—є трикутник, якщо:
- один із його кутів дорівнює сумі двох інших;
- один із його кутів більший від суми двох інших;
- один із його кутів менший від суми двох інших?
IV. Засвоєння знань
План вивчення нового матеріалу
- Уявлення про подібні фігури.
- Означення подібних трикутників.
- Властивості відповідних елементів подібних трикутників.
- Перша ознака подібних трикутників.
Означення. Два трикутники називаються подібними, якщо кути одного з них відповідно дорівнюють кутам іншого і відповідні сторони цих трикутників пропорційні:
![]() або
або ![]() :
:![]() :
:![]() .
.
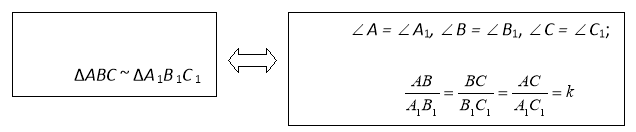
k—коефіцієнт подібності.
Задача 1. Відомо, що ΔАВС ~ ΔKMN. Назвіть відповідно рівні кути цих трикутників.
( ![]() )
)
Властивості подібних трикутників
1. Якщо ΔАВС ~ ΔА1В1С1 і ![]() , то
, то 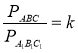
Ознаки подібності трикутників
Якщо в ΔАВС і ΔA1B1C1: ![]() A =
A = ![]() A1,
A1, ![]() B =
B = ![]() B1
B1 ![]() ΔАВС ~ ΔA1B1C1:
ΔАВС ~ ΔA1B1C1:
V. Формування первинних умінь
Виконання усних вправ (робота в парах)
«Спіймай помилку» ( діти читають завдання і відповідь на нього та знаходять помилки)
-
Трикутник АВС і трикутник з вершинами D, E, F подібні, причому
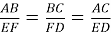 . Закінчіть запис
. Закінчіть запис 
![]()
(![]() )
)
- Чи можуть бути подібними прямокутний і тупокутний трикутники?
Так.
( Ні, бо в прямокутному і тупокутному трикутниках не можуть бути рівними всі кути)
- Два трикутники подібні з коефіцієнтом 0,25. У скільки разів сторони одного трикутника більші за відповідні сторони іншого?
Сторони одного трикутника в 25 разів більші за сторони іншого.
( У 4 рази сторони одного трикутника більші за відповідні сторони іншого трикутника)
Виконання письмових вправ
«Показова відповідь» (один з кращих учнів розв’язує задачу біля дошки із всіма поясненнями)
- (№326) На рисунку 4 ΔАВС ~ ΔА1В1С1. За даними рисунка знайдіть х і у.
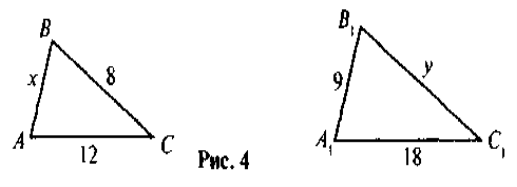
Розв’язання: 1) 18:12=1,5
2) 8*1,5=12 (см)
3) 9:1,5=6 (см).
Відповідь: 12 см, 6 см.
- (№328) Пряма КМ паралельна стороні АС трикутника АВС (рис.). знайдіть відрізок МС, якщо:
1) АК=2 см, КВ=6 см, ВМ=9 см.
2) АК:КВ=2:3, ВС=10 см.
Розв’язання: АВ=2+6=8 см
![]() ,
,![]() , х=8*9/6=12 см—СВ.
, х=8*9/6=12 см—СВ.
МС=СВ-ВМ=12-9=3 см.
Відповідь: МС=3 см.
- (№332) Сторони трикутника дорівнюють 2,5 см, 4 см і 5 см. Знайдіть сторони трикутника, подібного даному, якщо:
а) його периметр дорівнює 46 см;
б) його найменша сторона дорівнює найбільшій стороні даного трикутника.
Розв’язання: Р=2,5+4+5=11,5 см-периметр даного трикутника
- Р1/Р=46/11,5=4-коефіцієнт пропорційності
2,5*4=10 см-одна сторона
4*4=16 см-друга сторона
5*4=20 см-третя сторона.
- 5 см-найменша сторона трикутника
5/2,5=2-коефіцієнт пропорційності
4*2=8 см-друга сторона
5*2=10 см-третя сторона
Відповідь: 1) 10 см, 16 см, 20 см.
2)5 см, 8 см, 10 см.
-
(№330) Відомо, що (
 . Знайдіть:
. Знайдіть:
а) кут С, якщо ![]() ;
;
б) кут ![]() , якщо
, якщо ![]() .
.
Розв’язання: ![]() ;
;
![]() ;
;
![]() .
.
Відповідь: ![]() .
.
- (№358 - а, б) на рисунку 104 знайдіть подібні трикутники і доведіть їх подібність.
Відповідь: ![]() ,
, ![]() ,
, ![]()
Усні вправи (додатково) «Спіймай помилку»
Два трикутники подібні. Чи відповідають цьому твердженню наведені умови?
-
Два трикутники одного трикутника дорівнюють
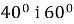 , а в іншому із трикутників є кут
, а в іншому із трикутників є кут 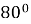 .
.
- Сторони одного із трикутників дорівнюють 1 м, 1,5 м, 2 м, а сторони іншого з трикутників дорівнюють 10 м, 15 м, 20 м.
VІ. Домашнє завдання
Опрацювати § 10,2, 11,1.
Виконати № 327, 329, 331*.
VІІ. Підведення підсумків уроку
«Опитування-підсумок»
Запитання до класу:
- Що на уроці було головним?
- Що нового сьогодні дізнались?
- Чому навчились?


про публікацію авторської розробки
Додати розробку
