«Площа паралелограма»
Конспект уроку
на тему:
«Функціональна залежність між величинами як математична модель реальних процесів. Функція. Область визначення та область значень функції. Способи задання функції. Графік функції. Лінійна функція її графік та властивості»
Підготувала вчитель-методист Кременецької ЗОШ І-ІІІ ст. №1
ім.Галини Гордасевич Алкіна Галина Володимирівна
Тема: Функціональна залежність між величинами як математична модель реальних процесів. Функція. Область визначення та область значень функції. Способи задання функції. Графік функції. Лінійна функція її графік та властивості
Мета:
навчальна:
- домогтися усвідомлення учнями змісту понять «функція», «функціональна залежність», «область визначення функції», «область значень функції», способи задання функції;
- сформувати в учнів свідоме розуміння поняття «графік функції» та розпочати роботу із засвоєння вмінь читати та будувати графіки функції;
- ознайомити учнів із означенням лінійної функції та сформувати знання про графік та властивості лінійної функції;
розвивальна:
- розвивати абстрактне мислення;
виховна:
- виховувати організованість, уважність та наполегливість.
Тип уроку: урок формування нових знань.
Обладнання та наочність: підручник з алгебри за 7 клас, автор: Істер, Нова програма
Хід уроку
І. Організаційний етап
Перевірка готовності класу до уроку
ІІ. Аналіз контрольної роботи
Оголошення оцінок, робота над помилками.
ІІІ. Формулювання мети й цілей уроку
IV. Мотивація навчальної діяльності
Виявляється, що як і в щоденному житті, так і в науці часто зустрічаються залежності між двома змінними, які можна виразити формулами або іншими способами і властивості таких залежностей дуже схожі на той приклад, що ми розглянули. Тому на сьогоднішньому уроці ми нарешті з’ясуємо, як такі залежності визначаються в математиці, які математичні поняття пов’язані із цим поняттям, а також навчимося розв’язувати контрольні завдання на закріплення змісту позначених понять.
V. Актуалізація опорних знань
2. Потяг рухається зі швидкістю 70 км/год. За t годин він долає S км. Задайте формулою залежність S від t.
3. Нехай a см — довжина ребра куба, а Vсм3 — його об’єм. Задайте формулою залежність V від a.
4. При яких значеннях змінної має зміст вираз: ![]() ;
; ![]() ;
; ![]() ?
?
VІ. Формування нових знань
Функція. Область визначення та область значень функції
План викладання навчального матеріалу:
1. Уявлення про залежність (відповідність) між двома змінними. Незалежна змінна. Залежна змінна
2. Функціональні залежності. Функції. Аргумент та значення функції
3. Способи задання функції: а) таблицею; б) формулою; в) графічно; г) опис
4. Область визначення та область значень функції
5. Приклад. Функція задана формулою ![]() .
.
|
Конспект Як знайти область визначення функції |
|||
|
№ |
Вид функції |
Формулювання |
Приклад |
|
1 |
Многочлен |
Область визначення: |
|
|
2 |
Цілий вираз |
Область визначення: |
|
|
3 |
Дробовий вираз (знаменник — буквений вираз) |
Область визначення: ті значення |
|
1) Яка змінна є аргументом? ![]() 2) Яка змінна є залежною?
2) Яка змінна є залежною? ![]()
3) Яке значення функції відповідає аргументу –2? [Якщо ![]() , то
, то ![]() ]
]
4) Якому значенню аргументу відповідає значення функції ![]() ? [
? [![]() , отже,
, отже, ![]() ,
, ![]() ]
]
Висновки. Дві найтиповіші задачі для функції: за відомим значенням аргументу відшукати відповідне значення функції - та обернена: знайти аргумент, що відповідає заданому значенню функції.
Графік функції
Означення. Графіком (числової) функції називається множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати — відповідним значенням функції, тобто
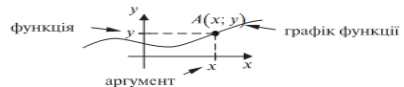
Покажемо, як можна побудувати графік функції, яку задано формулою.
Нехай функцію задано формулою ![]() , де
, де ![]() .
.
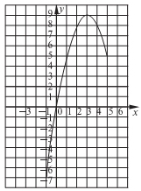
Складемо таблицю деяких відповідних значень аргументу й функції:
|
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
–7 |
0 |
5 |
8 |
9 |
8 |
5 |
Позначимо на координатній площині точки, координати яких указано в таблиці. З’єднаємо їх плавною лінією (рис.) Дістанемо графік функції, заданої формулою ![]() , де
, де ![]() . Чим більше позначимо точок, що належать графіку, і чим щільніше вони будуть розташовані, тим точніше буде побудовано графік функції.
. Чим більше позначимо точок, що належать графіку, і чим щільніше вони будуть розташовані, тим точніше буде побудовано графік функції.
Лінійна функція, її графік та властивості
Викладання матеріалу за планом:
1. Приклади величин, зв’язок між якими виражається функцією вигляду ![]() .
.
2. Означення лінійної функції.
3. Властивості лінійної функції (область визначення та область значень).
4. Графік лінійної функції загального вигляду (геометричний зміст). Зв’язок положення графіка лінійної функції із коефіцієнтами ![]() та
та ![]() .
.
|
Конспект Лінійна функція та її графік
1. Означення. Функція, яку можна задати формулою Приклад:
2. Властивості лінійної функції 1) Область визначення — будь-яке число. 2) Область значень — будь-яке число. 3. Графік функції — пряма. Щоб побудувати графік, шукаємо координати будь-яких двох його точок.
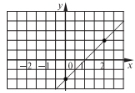
Приклад. Побудувати графік функції
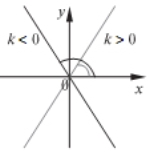
4. Властивості графіка лінійної функції
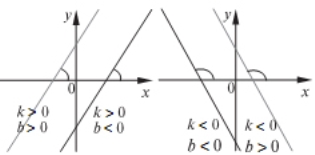
• Якщо
• Якщо
• Число |
|
Конспект Залежність між розташуванням прямої |
||
|
1) |
2) |
3) |
|
|
|
|
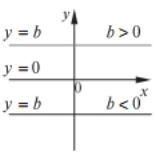
Якщо ![]() , графік лінійної функції збігається з віссю
, графік лінійної функції збігається з віссю ![]() (рівняння осі
(рівняння осі ![]() :
: ![]() ).
).
Але вісь ![]() не є графіком жодної лінійної (і взагалі жодної) функції, бо для цього не виконується визначення функції (одному значенню аргументу відповідає не одне, а безліч значень функції).
не є графіком жодної лінійної (і взагалі жодної) функції, бо для цього не виконується визначення функції (одному значенню аргументу відповідає не одне, а безліч значень функції).
Конспект Взаємне розташування графіків двох лінійних функцій
Дано функції: ![]() , графік — пряма
, графік — пряма ![]() ;
;
![]() , графік — пряма
, графік — пряма ![]() .
.

VII. Підсумки уроку
Використовуючи план уроку та опорний конспект, учні проговорюють навчальний матеріал, з’ясовують, яка частина навчального матеріалу була найскладнішою, яка найпростішою, що не зрозуміло.
VIII. Домашнє завдання
Вивчити означення основних понять уроку, опрацювати конспект, §17-19.


про публікацію авторської розробки
Додати розробку