Урок-подорож . Алгебра 10 клас. Співвідношення між тригонометричними функціями одного аргументу.

Алгебра 10 клас

Розробка уроку за темою “Співвідношення між тригонометричними функціями одного аргументу. Розв'язування задач".

Мета:  "Формувати знання, уміння та навички учнів у застосуванні властивостей та формул співвідношення між тригонометричними функціями до розв'язування задач. Розвивати уміння аналізувати, синтезувати, робити висновки. Сприяти розвитку фантазії, гнучкості мислення, виховувати волю та наполегливість у навчанні. Виховувати інтерес до вивчення предмета."

Обладнання: картки для індивідуальної роботи, презентація, музичний супровід, карта подорожі, рятівні круги , формули співвідношень між тригонометричними функціями одного аргументу

Урок-подорож

1. Вступна частина. Організаційний момент.

Учитель: Блез Паскаль сказав "Предмет математики настільки серйозний,що  не можна упускати випадку, щоб зробити його більш привабливішим." Наш сьогоднішній урок ми проведемо у формі кругосвітньої морської подорожі у країну "Тригонометрія". Під гаслом(на стіні текст)"Боротися й шукати, знайти і не здаватися"

Ви знаєте, як довго та старанно готувалися експедиції до плавання, як готували оснастку, прискіпливо підбирали команду. Перед виходом у море перевіряли роботу усіх вузлів та механізмів корабля, заправку пальним та продуктами харчування. Екіпаж екзаменували. А у нас – це перевірка вивченого та засвоєного матеріалу. Вдало завершивши, нашу морську подорож, ми повинні узагальнити отриманні знання з даної теми. Для нашого корабля потрібно обрати капітана, надійного та знаючого свою справу.  (Учні пропонують ім'я капітана та 2 боцманів)

Капітану пропонується відповісти на запитання:

1. Які тригонометричні відношення ви знаєте?
2. Що ми називаємо тангенсом?
3. Який вигляд має тригонометрична одиниця?

А тепер проекзаменуємо команду (боцманів)

1. Які з тригонометричних функцій є парними та непарними?
2. Як за графіком розпізнати парні та непарні функції?
3. Які ви знаєте одиниці вимірювання кутів?
4. Скільки градусів містить 1 радіан?

Та нарешті перевіримо готовність екіпажу

Усно. Розглянути приклади, записані на дошці. За правильні відповіді боцмани видають 1 рятівний круг.

1. виразити в радіанній мірі

45˚                              120˚;                                270˚

     б)   виразити в градусній мірі

;          3;       ;

     в) визначити знак

;                                ;                            

     г) обчислити

         2͘͘∙sin 30˚+ 3cos 60˚ - 2tg 45˚ + ctg 310˚= 2 ∙ + 3 ∙ – 2 ∙ 1 + = 1 + 1,5 – 2 + √3 = 0,5 +   √3.

     д) Знайти помилку! sin 128˚ ∙ cos 200˚ ∙ ctg 260˚ tg 300˚ < 0

Отже, екіпаж готовий до відплиття, перша зміна може заступати на вахту. Ми вирушаємо у плавання, то бажаємо усім  "Сім футів під кілем!" А в бортових журналах запишемо дату відправлення та маршрут нашої подорожі ( число і тема).  4 учнів працюють  індивідуально,  2 + 2 на контролі.

Ми підходимо до мису "Обчислювальний." В незнайомих бухтах викликають лоцмана, який проводить корабель між рифами.

Завдання для лоцманів: (2є біля дошки)

1. Дослідити на парність

а) у(х) = ; +                б) у(х) = tgx + ctgx= -(thx + ctgx) –

2. a) y(x) = = = y(x) +                    б) y(x) = ∙ cosx –

Решта класу працює "в парах"

        а) Обчислити: 6 sin – 2cos + tg – 7 ctg = 6 ∙ – 2 ∙  + 1 – 7 = 3 – 1 + 1 – 7 = - 4.

        б) sin 45˚ ∙ cos 60˚ ∙ ctg 30˚ = ∙ ∙ = ;

Ми вдало обігнули мис "Обчислювальний" і входимо в затоку "Озадачена"  і знову нам потрібна допомога лоцманів, які проведуть нас по затоці.

6 учнів розв'язують приклади на дошці, лоцмани перевіряють.

1. Спростити вираз

а) t + t + t = ;

б)   = = ;

2. а)cos ∙ tg = cos ∙ = sin ;

          б) + tg ∙ ctg = + 1 = 1 + =

      3. а) (sin+ (sin – cos = + 2 sin cos + + + – 2 sin= 2( + = 2

         б) ∙ = ∙ = 1.

4. a) sin 2 ∙ ctg 2 = sin 2 = cos 2 ;

б) (1 + = 1 + 2tg + + 1 – 2 tg+ = 2 + 2;

5. a) (tg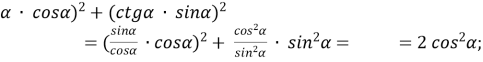

б)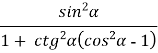 = = 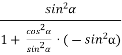= = 1.

6. a) 1 – ∙ = 2

б) – 1 = = =

Перед входом у затоку " Озадачена" , там нас зустрічає маяк "Дружній". А ми тим часом дружно працюємо і розв'яжемо задачу.

sin,       . Знайти: cos , tg , ctg.

cos = - = - ;    tg = - : (- ) = ;   ctg .

Після зміни команда зібралася у кают – компанії. Розминка – ерудит.

Що означають слова та вирази.

1. Ватерлінія, 2. Ескадра, 3. У чому вимірюється відстань на морі? ( 1 міля – 1852 км),  4. У яких одиницях вимірюється швидкість судів ( вузел, міля/год), 

5. Як на морській термінології звучать слова: кухня -  камбуз , вікно - ілюмінатор , мотузка – канат, повар – кок,стілець– банка, колокол – ринда, житлова кімната – каюта, кубрик.

6. Загадка.

7. У якій професії передбачено щогодини 6 хвилин мовчання? (радисти) і для чого?

Нам залишилось обійти півострів "   Спрощень  " та згадати ще раз той теоретичний матеріал, що було використано сьогодні на уроці.

Переглянути презентацію

Капітан: Увага! Бачу землю. Справа по борту "Країна Тригонометрія." Віддати швартови!

Учитель:  Наша подорож наближається до кінця. Підводячи підсумки хочеться відмітити участь усіх членів екіпажу під час подорожі. Оцінюється робота учнів на уроці.

Отже, наша подорож закінчується, але з синусами, косинусами, тангенсами і котангенсами ми не прощаємось, вони будуть супроводжувати нас під час навчання.

На останок я хочу вам сказати -  не зупиняйтеся на досягнутому, не лякайтесь труднощів, не сподівайтесь на чужий рятівний круг.

Дякую усім за урок.