Урок " ПОХІДНА ФУНКЦІЇ, ЇЇ ГЕОМЕТРИЧНИЙ ТА ФІЗИЧНИЙ ЗМІСТ."

УРОК №_____

ПОХІДНА ФУНКЦІЇ, ЇЇ ГЕОМЕТРИЧНИЙ ТА ФІЗИЧНИЙ ЗМІСТ

Формування компетентностей:

✵ предметна компетентність: домогтися засвоєння поняття похідної; сформувати поняття про геометричний та фізичний зміст похідної; сформувати вміння знаходити кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці, знаходити швидкість зміни величини в точці;

ключові компетентності:

✵ інформаційно-цифрова компетентність — діяти за алгоритмом та складати алгоритми;

✵ основні компетентності у природничих науках і технологіях — розпізнавати проблеми, які можна розв'язати засобами математики;

Тип уроку: засвоєння нових знань і вмінь.

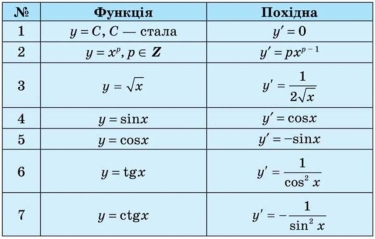
Обладнання та наочність:опорний конспект, табличка похідних, підручник.

Хід уроку

I. ОРГАНІЗАЦІЙНИЙ ЕТАП

II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

1. Перевірка завдання, заданого за підручником_____________

2. Виконання тестових завдань із подальшою самоперевіркою і самооцінюванням

Варіант 1

1) Знайдіть приріст функції f(х) = x - 1, якщо х₀ = 1, Δх = 0,1.

А. -0,1. Б. 0,1. В. -0,9. Г. 0,9.

2) Знайдіть приріст функції f(х) = 2х + 3 на відрізку [0;0,5].

А. -2. Б. 2. В. 1. Г. -1.

Варіант 2

1) Знайдіть приріст функції f(х) = 1 - x, якщо х₀ = 1, Δх = 0,1.

А. 0,9. Б. 0,1. В. -0,9. Г. -0,1.

2) Знайдіть приріст функції f(x) = -2x + 3 на відрізку [0;0,5].

А. -2. Б. -1. В. 1. Г. 2.

Відповіді

Варіант 1. 1) Б. 2) В.

Варіант 2. 1) Г. 2) Б.

ІІІ. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

План вивчення теми

1. Означення похідної.

2. Геометричний зміст похідної. Кутовий коефіцієнт і кут нахилу дотичної до графіка функції в заданій точці.

3. Фізичний зміст похідної Швидкість та прискорення прямолінійного руху.

4. Яку функцію називають диференційовною в точці? на проміжку?

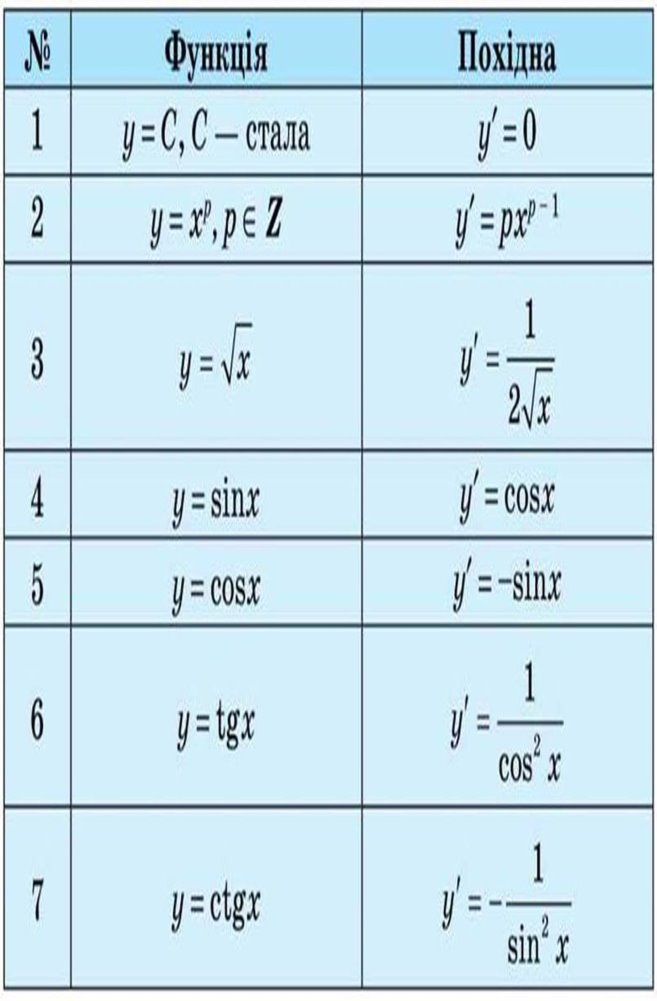
5. Застосування означення похідної до обґрунтування формул для обчислення похідних деяких функцій (f(х) = c (c — стала);  тощо).

IV. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І СПОСОБІВ ДІЙ

Похідна функції, її геометричний і фізичний зміст

Похідною функціїу = f(x) в точці х_о називається границя відно­шення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля, а границя існує, тобто

Функцію, яка має похідну в точці х_о, називають диферен­ційованою в цій точці.

Функцію, яка має похідну в кожній точці деякого проміжку, називають диференційованою на цьому проміжку. Операція знаходження похідної називається диференціюванням.

Похідна складеної функції у = f(g(x)) знаходиться за формулою

або похідна складеної функції дорівнює похідній зовнішній функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргу­менту.

Фізичний зміст похідної

Похідна функції в заданій точці – швидкість зміни функції в заданій точці.

Якщо матеріальна точка рухається прямо­лінійно і її координата змінюється по закону s = s(t), то швидкість її руху v(t) в момент часу t дорівнює похідній s'(t):

прискорення цієї матеріальної точки дорівнює похідній другого порядку від закону руху

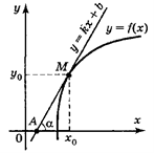Геометричний зміст похідної

Значення похідної функції у = f(x) в точці x_o дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x_o:

Рівняння дотичної до кривої

у = f(x) в точці М(x_o; у_o) має вигляд:

V. ЗАСТОСУВАННЯ ЗНАНЬ І ВМІНЬ

1. Робота з підручником

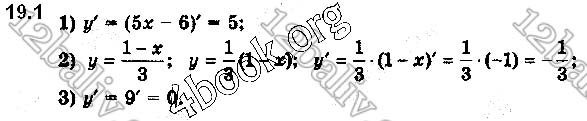
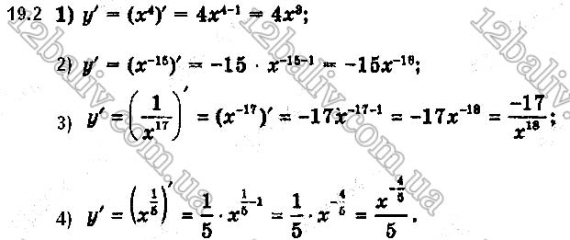
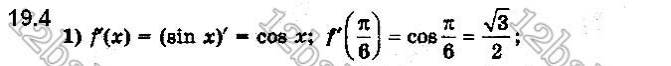
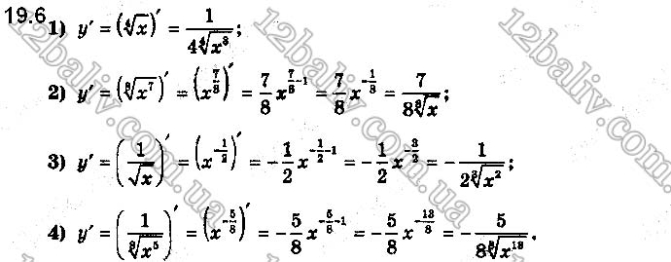
Функцію задано формулою f(x) = x².

1) Знайдіть похідну функції f(x).

2) Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка функції f(х) у точці х₀ = 1.

VI. ПІДБИТТЯ ПІДСУМКІВ УРОКУ, РЕФЛЕКСІЯ

VII. ДОМАШНЄ ЗАВДАННЯ

1. Завдання за підручником: __________________________

2. Додаткове завдання. Функцію задано формулою f(x) = x².

1) Знайдіть похідну функції f(x).

2) Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка функції f(х) у точці х₀ = 1.