Методична розробка уроку на тему: " Паралельне проектування та його властивості"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема уроку: Паралельне проектування та його властивості

 

Мета уроку:

• ознайомити учнів з поняттям паралельного проектування та його властивостями;
• розвивати просторову уяву; показати широке коло застосування властивостей паралельного проектування у навколишньому світі; розширювати загальний кругозір учнів.
• виховувати інтерес до вивчення даної теми та самостійність учнів.

Очікувані результати: учні повинні мати уявлення про паралельне проектування та його властивості.

 

Основні поняття: площина проекції, напрямок проектування, паралельна проекція

 

Тип уроку: урок вивчення нового матеріалу.

 

Методи уроку: бесіда, демонстрація наочних засобів навчання.

 

Обладнання: Моделі просторових фігур, ноутбук,  комп’ютерний проектор, презентація викладача з підтримкою Microsoft Office Power Point.

 

Міжпредметні зв’язки: астрономія (тема «Земля і місяць. Затемнення», фізика (тема «Відбивання світла»), екологія (тема «Переробка сміття»), художня культура (тема «Відродження»), будівельне креслення (теми «Прикладні геометричні побудови на площині», «Креслення в аксонометричних проекціях»).

Структура уроку.

1.               Організаційний момент
2.               Актуалізація опорних знань
3.               Мотивація навчальної діяльності
4.               Повідомлення теми і мети уроку
5.               Формування нових знань:

Паралельне проектування та його властивості. Лекція з елементами бесіди.

6.               Цікава сторінка.  Доповідь учня.
7.               Підведення підсумків уроку. Графічний диктант.
8.               Домашнє завдання.

 

Хід уроку.

1.               ОРГАНІЗАЦІЙНИЙ МОМЕНТ.
2.               АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ.

 

Показ мультиплікаційного фільму «Лунтік і його друзі» - 207 серія. Тінь

 

 

 

 

 

 

 

 

 

 

 

 

Запитання до учнів:

Викладач: Що означає слово «Стереометрія»?

Учень: Стереометрія – це розділ геометрії, який вивчає геометричні тіла у просторі.

Викладач: Які основні поняття «Стереометрії»?

Учень: основними поняттями стереометрії є – точка, пряма, площина.

Викладач: Які фігури ми вивчаємо в «Стереометрії»?

Учень: об’ємні

Викладач: Чому утворилася «тінь»?

Учень: Тому, що світло не проходить через тіла.

Викладач: Як виглядає тінь об’ємної фігури на площину? (з переглянутого мультика)

Учень: Вона є пласкою.

 

3. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ

Викладач: Художник малює картину, конструктор креслить креслення, фотограф фотографує, і водночас всі вони виконують одну справу - відображають просторові фігури на аркуші (площині). Процес відображення точок простору на площину називається проектуванням.  Зображення, що отримується при проектуванні називається проекцією.

Слово проекція виникло від латинського projection - кидання вперед, вдалину. Щось схоже на проекцію можна спостерігати, розглядаючи тінь, що відкидається предметом на поверхню стіни або підлоги при освітленні цього предмета джерелом світла. Для правильного зображення на площині плоских геометричних фігур, розташованих у просторі, необхідно знати та вміти використовувати закони паралельного проектування. Жодне зображення на кресленні, на картині, тим більше – при фото чи кінозйомці не порушує цих законів.

 

4.              ПОВІДОМЛЕННЯ ТЕМИ І МЕТИ УРОКУ

Викладач: Тема нашого уроку «Паралельне проектування та його властивості». Сьогодні на уроці ми з вами ознайомимося з поняттям паралельного проектування та навчимося будувати зображення просторових фігур на площині

 

5. ФОРМУВАННЯ НОВИХ ЗНАНЬ

Паралельне проектування та його властивості

Розповідь викладача.

Для зображення просторових фігур у стереометрії користуються па­ралельним проектуванням. Пригадаємо, що це таке.

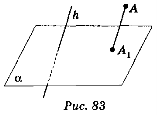
Нехай дано довільну площину α, точку А (рис. 83) і пряму h, яке перетинає площину α. Проведемо через точку А пряму, яка паралельна h, вона перетинає площину α у деякій точці А₁. Знайдену таким способом точку А; називають паралельною проекцією точки А на площину α у напрямі h. Пряму h називають проектуючою прямою, площину α — площиною проекцій.

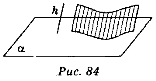Щоб побудувати проекцію будь-якої фігури, треба спроектувати на площину проекції кожну точку даної фігури (рис. 84). Наведемо деякі властивості паралельного проектування.

Теорема5. ( Г.П.Безв, В.Г.Бевз «Математика 10 кл.»,  ст.177)

Якщо відрізки, які проектуються, не паралельні проектуючій прямій, то при паралельному проектуванні:

1.                   відрізки фігури зображаються відрізками;
2.                   паралельні відрізки –  паралельними відрізками або відрізками однієї прямої;
3.                   довжини проекцій паралельних відрізків або  відрізків однієї прямої відносяться, як довжини проектованих відрізків.

 

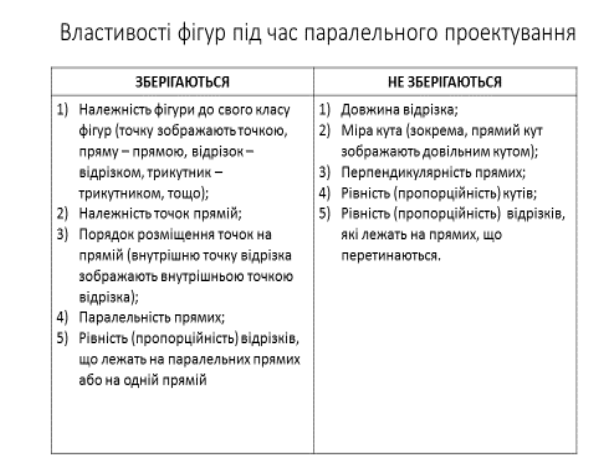
З наведених властивостей випливає, що під час паралельного проектування деякі властивості фігур зберігаються, а деякі – ні. Розглянемо таблицю.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зображення просторових фігур на площині

Розповідь викладача

Розглянуті властивості паралельного проектування дають змогу наочно зображати просторові фігури на площині.

 

Означення: Зображенням фігури називається будь-яка фігура, подібна до паралельної проекції даної фігури на деяку площину.

 

Алгоритм побудови:

Щоб побудувати паралельну проекцію многогранника необхідно

1.                   З’ясувати , як будуть зображатися усі його грані.

1.1.Щоб побудувати паралельну проекцію плоскої фігури, спочатку побудуйте її оригінал. Потім, спираючись на оригінал, виділіть властивості фігури :

•                     Які зберігаються під час паралельного проектування (на них треба спиратись, будуючи проекцію);
•                     Які не зберігаються під час паралельного проектування ( їх не можна використовувати, будуючи проекцію)

2.                   Послідовно виконати побудову кожної з граней

 

6. ЦІКАВА СТОРІНКА. Доповідь  учня.

 

 

 

7.          ПІДВЕДЕННЯ ПІДСУМКІВ УРОКУ:

Графічний диктант

8.          ДОМАШНЄ ЗАВДАННЯ. 

Г.П.Безв, В.Г.Бевз «Математика 10 кл.», №2 ст.178

Заключне слово викладача.

Сьогодні на уроці мені допомагали та гарно працювали протягом уроку такі учні: (прізвища учнів).

І на закінчення уроку пропоную переглянути відеоролик «Театр тіней »  Всім дякую.

               

 

 

 

 

 

 

Додаток 1

 

 

План-конспект уроку до теми:

«Паралельне проектування та його властивості» ( для учнів)

 

1. Поняття паралельної проекції.

 

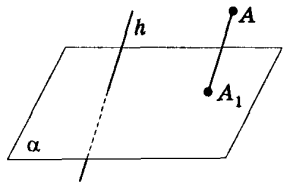Нехай дано довільну площину α, точку А  і пряму h, яке перетинає площину α. Проведемо через точку А пряму, яка паралельна h, вона перетинає площину α у деякій точці А₁. Знайдену таким способом точку А; називають паралельною проекцією точки А на площину α у напрямі h. Пряму h називають проектуючою  прямою, площину α — площиною проекцій.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

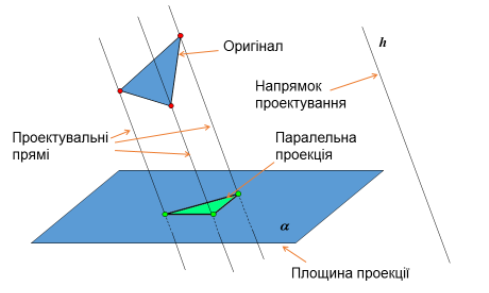
2. Властивості паралельного проектування

 

Теорема5. ( Г.П.Бевз «Математика», ст.177)

 

Якщо відрізки, які проектуються, не паралельні проектуючій прямій, то при паралельному проектуванні:

4. відрізки фігури зображаються відрізками;
5. паралельні відрізки –  паралельними відрізками або відрізками однієї прямої;
6. довжини проекцій паралельних відрізків або  відрізків однієї прямої відносяться, як довжини проектованих відрізків.

 

 

3. Зображення геометричних фігур

 

Означення: Зображенням фігури називається будь-яка фігура, подібна до паралельної проекції даної фігури на деяку площину.

 

Алгоритм побудови:

Щоб побудувати паралельну проекцію многогранника необхідно

3. З’ясувати , як збудуть зображатися усі його грані.

1.1.Щоб побудувати паралельну проекцію плоскої фігури, спочатку побудуйте її оригінал. Потім, спираючись на оригінал, виділіть властивості фігури :

• Які зберігаються під час паралельного проектування ( на них треба спиратись, будуючи проекцію);
• Які не зберігаються під час паралельного проектування ( їх не можна використовувати, будуючи проекцію)

4. Послідовно виконати побудову кожної з граней

Додаток 2

Тест до теми :

«Паралельне проектування та його властивості» (графічний диктант)

 

Чи правильними є твердження?

 

1.               Паралельною проекцією точки є точка.

 

2.               Паралельною проекцією прямої обов’язково є пряма.

 

3.               При паралельному проектуванні паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої.

 

4.               При паралельному проектуванні довжина відрізків зберігається.

 

5.               При паралельному проектуванні величина кутів зберігається.

 

Відрізок А₁B₁ — паралельна проекція відрізка АВ на площину α (рис.). Точка С лежить на відрізку АВ. Укажіть, які з наведених тверджень правильні, а які — неправильні:

 

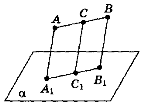6.               проекція точки С на площину α не належить відрізку А₁B₁;

 

7.               відрізки АВ і А₁В₁ не лежать в одній площині;

 

8.               якщо AC : BC = 2 : 3, то А₁C₁ : С₁В₁ = 2 : 3;

 

9.               якщо АС = СВ, то А₁С₁ = 2С₁В₁;

 

10.          якщо АС = 3 см, АВ =12 см, то А₁С₁ : А₁В₁ =1: 4.

 

 

Примітка.

Уважно прочитайте  завдання і виберіть правильну відповідь. Якщо ви згодні з твердженням ставите +, якщо ні – у бланк під номером питання.

 

1	2	3	4	5	6	7	8	9	10

 

Термін виконання:   5 хв.

Шкала оцінювання: за кожну правильну відповідь 1 бал. Сума балів відповідає оцінці за 12 бальною системою.

 

 

 

 

Відповіді до графічного диктанту:

 

1	2	3	4	5	6	7	8	9	10
+	-	+	-	-	-	-	+	-	+