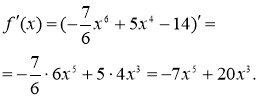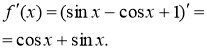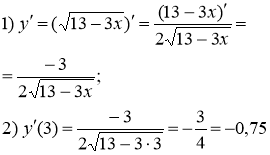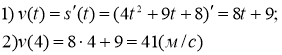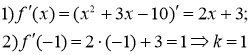Урок "Похідна та її застосування"
МЕТОДИЧНА РОЗРОБКА
відкритого практичного заняття
з дисципліни «Математика»
Зміст
|
Передмова |
6 |
|
|
1. |
План заняття |
7 |
|
2. |
Хід і зміст заняття |
9 |
|
2.1. |
Організаційний момент |
9 |
|
2.2. |
Ознайомлення студентів з темою та навчальними цілями заняття. Мотивація навчання. |
9 |
|
2.3. |
Систематизація і узагальнення теоретичних знань |
9 |
|
2.4. |
Застосування знань в стандартних умовах |
12 |
|
2.5. |
Застосування знань в нових умовах |
14 |
|
2.6. |
Підведення підсумків заняття |
16 |
|
2.7. |
Повідомлення домашнього завдання |
16 |
|
Додаток А |
|
|
|
Додаток Б |
|
|
|
Додаток В |
|
|
|
Додаток Г |
|
|
|
Додаток Д |
|
|
|
Слайди презентації |
|
|
Передмова
На сучасному рівні розвитку цивілізації особливу роль відіграє інноваційний потенціал суспільства, що потребує спеціалістів, здатних системно й конструктивно мислити, швидко знаходити потрібну інформацію, приймати адекватні рішення, створювати принципово нові ідеї в різних галузях знань. А це, в свою чергу, формує соціальне замовлення на нові підходи в системі освіти, нове педагогічне мислення, нове ставлення педагога до своєї діяльності, результатом якої має бути виховання «інноваційної людини».
Представлена методична розробка з теми «Похідна та її застосування» дає можливість познайомитись з застосуванням різних педагогічних технологій: технологія модульного навчання, квест-технологія, технологія кооперативного навчання, інформаційно-комунікаційні технології. Модульне навчання характеризується випереджаючим вивченням теоретичного матеріалу укрупненими блоками-модулями, алгоритмізацією навчальної діяльності, завершеністю і узгодженістю циклів пізнання та інших циклів діяльності. Дана робота являє собою розробку одного заняття, що завершує вивчення теми «Похідна та її застосування», і спрямоване на вирішення наступних завдань:
а) повторення, узагальнення і систематизація знань, умінь і навичок студентів;
б) формування уявлення про роль похідної в інших науках;
в) контроль і корекцію знань здобувачів освіти з вивченої теми;
г) розвиток пошукової діяльності із залученням різних джерел (виконання веб-квесту при підготовці до проведення заняття).
Матеріали заняття розраховані на учнів 10 класу. У розробці застосовується система рейтингової оцінки знань і умінь студентів, що переводиться у дванадцятибальну систему. Студенти ознайомлюються з усіма вимогами заняття і критеріями оцінок за різні види робіт на початку заняття.
Проведення заняття ведеться у відповідності до технологічної карти заняття, супроводжується слайдами презентації, мотивується різними фактами застосування похідної в різних галузях науки і виробництва.
Представлена методична розробка практичного заняття демонструє один з варіантів узагальнення теми «Похідна та її застосування», допомагає спонукати учнів до самостійного мислення й ухвалення рішень.
ПЛАН ЗАНЯТТЯ
Дисципліна: Математика
Тема заняття: Похідна та її застосування
Мета заняття:
Методична – впроваджувати сучасні педагогічні технології (технологію модульного навчання, квест-технологію, технологію кооперативного навчання, інформаційно-комунікаційні технології) для створення умов, що дозволяють кожному студенту розкрити свій творчий потенціал, пізнавальну активність, проявляти ініціативу і самостійність;
Навчальна – узагальнити і систематизувати знання про похідну, її фізичний, геометричний та економічний зміст; формувати навички застосування знань до розв’язання задач на екстремуми; удосконалювати вміння та навички самостійно отримувати нові знання за джерелами; підвести студентів до розуміння того, що знання поняття похідної необхідно людству в їх житті; удосконалювати вміння ясно, логічно і точно викладати свою точку зору;
Розвиваюча – створювати умови для розвитку позитивної мотивації до навчання, стимулювати розвиток творчих можливостей; розвивати здатність до самостійної інформаційно-пізнавальної діяльності, формувати основні уміння опрацювання інформації, навички дослідницької роботи, проведення самоконтролю і взаємоконтролю;
Виховна – навчати об’єктивній оцінці своїх можливостей і успіхів; сприяти розвитку навичок усного мовлення, вмінню грамотно вести діалог і аргументувати свої дії; усвідомлення великої практичної значущості похідної в житті людини; формувати вміння працювати в команді.
Вид заняття : практичне заняття
Тип заняття : узагальнення і систематизація знань, умінь та навичок
Форми і методи роботи на занятті:
- організаційні: індивідуальна, групова (робота в парі, робота в групі), колективна (фронтальна);
- методи навчання: словесні (бесіда); наочні: комп’ютерна презентація; інтерактивні: вправа «мікрофон»; практичні: дослідницький, пошуковий, організація застосування похідної при вирішенні математичних, фізичних, хімічних, економічних задач;
- методи контролю і самоконтролю: усний контроль, самоконтроль, взаємоконтроль.
Методичне забезпечення:
- Технологічна карта заняття;
- Таблиці «Похідна», «Застосування похідної»;
- Картки контролю теоретичних знань (картки з друкованою основою) картки «Знайди пару» (перевірка таблиці похідних), лист оцінювання;
- Презентація заняття.
Технічні засоби навчання:
- Мультимедійний проектор
- Персональний комп’ютер
Міжпредметні зв’язки:
Забезпечуючі: «Українська мова», «Фізика», «Інформатика».
Забезпечуємі: «Природничі науки», «Економіка підприємства», «Фінанси підприємства», «Політична економія», «Гроші та кредит», «Інформаційні системи і технології у фінансово-кредитних установах».
Література
Основна:
1. Бевз Г. П.Математика : Алгебра і початки аналізу та геометрія. Рівень стандарту) : підруч. для 10 кл. закладів загальної середньої освіти / Г. П. Бевз, В. Г. Бевз. — К. : Видавничий дім «Освіта», 2018. – 288 с. : іл.
2. Бурда М.І. Математика (алгебра і початки аналізу та геометрія, рівень стандарту : підруч. для 10 кл. закладів загальної середньої освіти / М.І. Бурда , Т.В. Колеснік, Ю.І.Мальований, Н.А.Тарасенкова. — К. : УОВЦ «Оріон», 2018. – 288 с. : іл.
3. Мерзляк А. Г. Математика : алгебра і початки аналізу та геометрія, рівень стандарту: підруч. для 10 кл. закладів загальної середньої освіти / А.Г. Мерзляк, Д.А.Номіровський, В. Б. Полонський, М.С.Якір. — Х. : Гімназія, 2018. 256с.: іл.
4. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К. Математика. Підручник. К., Вища школа, 2001
5. Нелін Є.П. Алгебра та початки аналізу: підручник для 10 класу загальн.учбових закладів. Х.: Гімназія, 2010
Додаткова :
1. Лейфура В.М. та ін. Математика: Підручник для студентів екон.спеціальн.вищих навч. закладів І-ІІ рівнів акредетації,/ В.М. Лейфура , Г.Г.Голодницький, Й.І.Файст; за ред. Лейфура В.М. - К.: Техніка, 2003.– 640 с. : іл.
2. Богомолов II.В. Практические занятия по математике. М.: Высш. шк., 1990
3. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики. К., Вища школа, 2001
4. Збірник заданий для державної підсумкової атестації з математики. 11 класс. Ред. З.І. Слєпкань. – Харьків, “Гімназія”, 2014
5. https://zno.osvita.ua/mathematics/
Хід і зміст заняття
1. Організаційний момент. 1 хв.
Привітання зі студентами
Відмітка у журналі відсутніх
Перевірка готовності до заняття студентів, аудиторії
2. Ознайомлення студентів з темою та навчальними цілями заняття. Мотивація навчання. 8 хв.
Мета. Формування на особистісно значимому рівні внутрішньої готовності до виконання нормативних вимог навчальної діяльності. Створення ділової атмосфери, позитивного настрою на активну діяльність і розумову роботу, включення в діловий ритм. Розширення уявлення студентів про зародження похідної.
Викладач. На першому занятті з вивчення похідної я вам запропонувала замислитися над питанням: «Ми вивчаємо похідну, а навіщо? Чи так це важливо в житті?» Ви не змогли на нього відповісти, так як у вас не вистачало відповідних знань з цієї теми. І тоді я вам запропонувала провести самостійне дослідження з теми «Похідна та її застосування» у різних галузях науки у вигляді виконання веб-квесту. (Додаток А) Для виконання цієї роботи була висунута гіпотеза: «Диференціальне числення – це опис навколишнього світу, виконаний на математичній мові. Похідна допомагає нам успішно вирішувати не тільки математичні завдання, а й практичні задачі різних галузей науки і техніки». В ході дослідницької роботи ви повинні були або підтвердити, або спростувати цю гіпотезу.
Сьогодні ми побачимо, наскільки успішно ви впоралися із завданням самостійного відбору та обробки інформації, покажемо практичну необхідність і теоретичну значимість теми «Похідна».
Тема нашого заняття «Похідна та її застосування». На ньому ми повторимо правила обчислення похідних, згадаємо таблицю похідних, познайомимось з історією виникнення похідної, основними напрямками її застосування в різних областях науки.
Протягом заняття вам необхідно буде заповнювати лист оцінювання Додаток Б), який дасть змогу оцінити рівень вашої підготовки з теми. Ви самостійно або в парі чи групі будете отримувати бали за виконання вправ у відповідності до правил переводу набраних балів в 12-бальну оцінку. (Слайд 2)
Хочу наголосити слова відомого вченого Фрідріха Енгельса: «Лише диференціальне числення дає можливість природознавству зображати математично не тільки стан, але і процес руху».
Давайте познайомимось з історичною сторінкою вашого дослідження, яку підготували студентки Горлач Ліза і Конева Дар’я. (Слайди 3-6)
3. Систематизація і узагальнення теоретичних знань. 22 хв.
Мета. Актуалізація опорних знань, удосконалення вмінь чітко, логічно і точно викладати свою точку зору; розвиток здатності до самостійного відтворення основних теоретичних положень теми «Похідна та її застосування»; перевірка рівня їх засвоєння.
Викладач. Переходимо до виконання другої сторінки вашого завдання. Слово надається теоретикам Моргун Юлії і Берднік Микола. (Слайд 7, 11)
1) Повторення основних тверджень про похідну проводиться у вигляді вправи «Мікрофон»: ведучі студенти задають вибраному студенту питання, пов’язане зі словом з підготовленого тезауруса теми.
- Що називають диференціюванням? (Операцію знаходження похідної функції називають диференціюванням)
- Що таке приріст аргументу? (Вираз х – х0 = х)
- Що таке приріст функції? (у = f(х0 + х) – f (х0))
- Дайте означення похідної (Похідною функції f(x) у точці x0 називають границю відношення приросту функції в точці x0 до приросту аргументу, якщо приріст аргументу прямує до нуля, а границя існує)
- В чому полягає геометричний зміст похідної? (Похідна – це кутовий коефіцієнт дотичної, проведеної до заданої точки)
- Як можна сформулювати фізичний зміст похідної?(Похідна – це миттєва швидкість)
- А з економічної точки зору похідна – це? (Похідна - це продуктивність праці, продуктивність праці вимірюється кількістю продукції, виконаної робітником впродовж деякого часу)
- Сформулюйте необхідну і достатню умову сталості функції (Функція f(х) є сталою на інтервалі (a; b) тоді і тільки тоді, коли її похідна дорівнює нулю в кожній точці цього інтервалу)
- Які точки називають критичними? (Внутрішні точки області визначення функції, у яких її похідна дорівнює нулю або не існує, називають критичними точками функції)
- Сформулюйте достатню умову зростання функції (Якщо в кожній точці інтервалу (a; b) її похідна f (х) > 0, то функція f(х) зростає на цьому проміжку)
- Сформулюйте достатню умову спадання функції (Якщо в кожній точці інтервалу (a; b) її похідна f (х) < 0, то функція f(х) спадає на цьому проміжку)
- Що таке точки екстремуму? (Точки максимуму і мінімуму називають точками екстремуму)
- Сформулюйте необхідну умову екстремуму функції (У точках екстремуму похідна функції дорівнює нулю або не існує)
- Сформулюйте достатню умову екстремуму функції (Якщо функція f(х) неперервна в точці х0 і похідна f (х) змінює знак при переході через точку х0, то точка х0 – точка екстремуму)
2) Перевірка знань теоретичного матеріалу проводиться у вигляді заповнення студентами картки з друкованою основою (Додаток В)
Відповідь:
Завдання. Заповніть картку з друкованою основою:
1. х – х0 = х - приріст аргументу
2. у = f(x0 + х) – f(x0) - приріст функції
3. Запишіть означення похідної у вигляді формули:
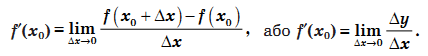
4. Геометричний зміст похідної: похідна – це кутовий коефіцієнт дотичної, проведеної в заданій точці x0 або тангенс кута нахилу дотичної в заданій точці x0
5. Похідна – це миттєва швидкість – це фізичний зміст похідної: v(t) = s(t),
a (t) = v(t) = s(t)
6. Функція f(x) зростає на інтервалі (a; b), якщо в кожній точці цього інтервалу її похідна f (х) > 0
7. Функція f(x) спадає на інтервалі (a; b), якщо в кожній точці цього інтервалу її похідна f (х) < 0
8. Внутрішні точки області функції, у яких похідна дорівнює нулю, або не існує називають критичними точками.
9. Функція f(x) є сталою на інтервалі (a; b), тоді і тільки тоді, коли f (x) = 0 в усіх точках цього інтервалу.
10. Точки максимуму і мінімуму називають точками екстремуму.
11. У точках екстремуму похідна функції дорівнює нулю, або не існує.
12. Якщо функція f(x) неперервна в точці x0 і похідна f (x) змінює знак при переході через точку x0, то точка x0 – точка екстремуму функції f(x).
13. Якщо неперервна функція у = f(x) має похідну, яка в точці x0 змінює знак з «+» на «– », то точка x0 – точка максимуму функції f(x).
14. Якщо неперервна функція у = f(x) має похідну, яка в точці x0 змінює знак з «– » на «+», то точка x0 – точка мінімуму функції f(x).
Перевірка проводиться у вигляді взаємоперевірки за відповіддю на слайді 9.
3) Вправа «Контейнер» (робота в парі). На слайді презентації записані формули. (Слайд 9).
1.![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. 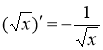 ;
;
5. ![]() ;
;
6.![]() ;
;
7. ![]() ;
;
8. ![]() ;
;
9. ![]() ;
;
10. ![]()
Відповідь: правильні формули 2, 3, 6, 7, 8, 9, 10, серед них правила диференціювання 2, 3, 6, 8, 10.
4) Вправа «Знайди пару». Перевірка знань таблиці похідних.
Виконується кожним студентом самостійно і перевіряється у вигляді взаємоперевірки і отримані бали виставляються у лист оцінювання.
Доберіть до кожної функції її похідну:
|
№ з/п |
Функція |
|
Похідна |
Відповідь: |
|
|
1 |
k |
А |
|
1 |
З |
|
2 |
xn |
Б |
– |
2 |
Е |
|
3 |
|
В |
|
3 |
І |
|
4 |
|
Г |
3х2 |
4 |
Ґ |
|
5 |
|
Ґ |
|
5 |
А |
|
6 |
|
Д |
|
6 |
Й |
|
7 |
|
Е |
|
7 |
Д |
|
8 |
|
Є |
|
8 |
Ї |
|
9 |
х3 |
Ж |
1 |
9 |
Г |
|
10 |
х2 |
З |
0 |
10 |
И |
|
11 |
х |
И |
2х |
11 |
Ж |
|
|
|
І |
|
|
|
|
|
|
Ї |
|
|
|
|
|
|
Й |
|
|
|
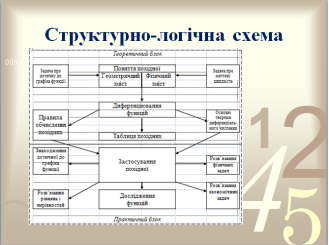
5) Розгляд структурно-логічної схеми теми «Похідна та її застосування», підготовлену теоретиками веб-квесту (Додаток В).
4. Застосування знань в стандартних умовах 20 хв.
"Просто знати - ще не все, знання потрібно використовувати".
Гете
Мета. Створення умов для застосування отриманих знань при вирішенні завдань з використанням формул і правил диференціювання, фізичного та геометричного змісту похідної; сприяння вихованню позитивного ставлення до знань і процесу навчання, впевненості у своїх силах.
Викладач. Переходимо до третьої сторінки нашого квесту. Аналітики Дорошенко Анастасія і Рибачук Ольга розкажуть нам про своє дослідження. (Слайд 12)
Виконання самостійної роботи студентами (15 хвилин):
|
№ з/п |
І варіант |
ІІ варіант |
|
1 |
а) (ЗНО 2018 основна сесія)
Укажіть похідну функції
А)
Б)
В)
Г)
Д) |
а) (ЗНО 2018 додаткова сесія)
Укажіть похідну функції
А)
Б)
В)
Г)
Д) |
|
|
б) (ЗНО 2017 основна сесія)
Укажіть похідну функції
А)
Б)
В)
Г)
Д) |
а) (ЗНО 2015 додаткова сесія)
Якщо
А)
В)
Д) |
|
2 |
(ЗНО 2015 основна сесія) Укажіть рівняння прямої, яка може бути дотичною до графіка функції у = f(x) у точці з абсцисою х0 = 2, якщо f (x) = -3:
А)
В)
Д) |
(ЗНО 2014 основна сесія) Укажіть рівняння прямої, яка може бути дотичною до графіка функції у = f(x) у точці з абсцисою х0 = 1, якщо f (х0) = 5, f (х0) = 2:
А)
В)
Д) |
|
3 |
(ЗНО 2016 основна сесія)
Обчисліть значення похідної функції |
(ЗНО 2016 додаткова сесія)
Матеріальна точка рухається прямолінійно за законом |
|
4 |
(ЗНО 2019 основна сесія)
Знайдіть похідну функції |
(ЗНО 2017 додаткова сесія)
Знайдіть похідну функції |
Відповіді:
1 варіант: 1а) А 1б) Д 2) Д 3) -0,75 4) ![]() ; х1 = 0,5; х2 =-0,5
; х1 = 0,5; х2 =-0,5
2 варіант: 1а) В 1б) Г 2) Д 3) 41 4) ![]() ; k = 1.
; k = 1.
Повний розв’язок самостійної роботи в додатку Д.
Перевірка здійснюється у вигляді самоперевірки за слайдами презентації (Слайд 13)
5. Застосування знань в нових умовах 20 хв.
Мета. Формування навчальної задачі; розвиток навичок спільної пошукової діяльності із залученням різних джерел; розвиток самостійності в плануванні і здійсненні навчальної діяльності та організації навчального співробітництва з педагогом та однолітками; розвиток мовленнєвих умінь і навичок.
Викладач. Переходимо до сторінки нашого веб-квесту «Практична». Послухаємо підготовлений матеріал студентів Сусли Діани і Шилова Антона. (Слайди 14-16)
Виконання задач на застосування похідної в економіці у групі. Студенти виконують задачі і та команда, яка першою виконала розв’язок задачі записує його на дошці і дає пояснення. Інші команди задають питання або вказують на допущені помилки.
Задача 1. Обсяг продукції u, вироблений бригадою робітників, може бути описаний рівнянням ![]() (од.) , 1< t <8, де t — робочий час у годинах. Обчислити продуктивність праці та швидкість її зміни через дві години після початку роботи.
(од.) , 1< t <8, де t — робочий час у годинах. Обчислити продуктивність праці та швидкість її зміни через дві години після початку роботи.
Розв’язок. Продуктивність праці — це похідна:
![]() (од./год),
(од./год),
![]()
а швидкість зміни продуктивності – відповідно задаються похідною z(t):
z(t)=-5t+15 (од./год2),
z(2)=-5∙2+15=-10 +15 = 5 (од./год2),
Відповідь: 120 од./год., 5од./год.2.
Задача 2. Витрати на виробництво продукції обсягу х задаються функцією ![]() . Виробник реалізує продукцію за ціною 25 ум.од. Знайдіть максимальний прибуток R і відповідний обсяг продукції х.
. Виробник реалізує продукцію за ціною 25 ум.од. Знайдіть максимальний прибуток R і відповідний обсяг продукції х.
Розв’язок:
|
План розв’язку |
Реалізація плану |
||||||||||||||||
|
Записуємо у вихідну формулу для обчислення величини, екстремальне значення якої треба знайти |
Прибуток дорівнює різниці між виручкою U і витратами С. R = U – С |
||||||||||||||||
|
Знаходимо відповідну функцію, залежну від х |
Реалізувавши продукцію обсягах за ціною 25 ум.од., підприємець має виручку
|
||||||||||||||||
|
Визначаємо (за змістом завдання) область визначення функції |
За змістом завдання обсяг продукції х може приймати будь-яке додатне значення, тобто |
||||||||||||||||
|
Сформулюємо математичну задачу |
Знайти найбільше значення функції |
||||||||||||||||
|
Функцію аргументу х досліджуємо на екстремум на знайденому проміжку |
критична точка функції х = 10
Похідна змінює свій знак при переході через цю точку з «+» на «–», значить х = 10 – точка максимуму.
|
||||||||||||||||
|
Інтерпретуємо результати і записуємо відповідь |
Максимальний прибуток, що дорівнює 96 ум.од., досягається при обсязі виробництва 10 ум. од. |
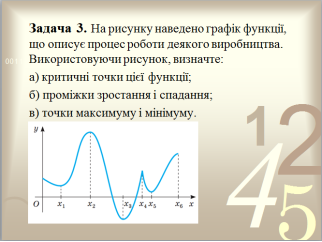
Задача 3. На рисунку наведено графік функції, що описує процес роботи деякого виробництва. Використовуючи рисунок, визначте:
а) критичні точки цієї функції;
б) проміжки зростання і спадання;
в) точки максимуму і мінімуму.
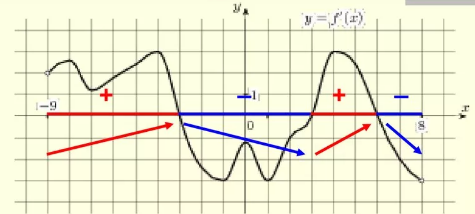
Творче завдання: у відповідності до цього графіка функції побудуйте графік похідної цієї функції.

Відповідь: а) критичні точки функції х1, х2, х3, х4, х5;
б) проміжки зростання: х [х1, х2] і [х3, х4] і [х5, х6];
спадання х [0, х1] і [х2, х3] і [х4, х5];
в) точки максимуму: х2, х4 і мінімуму: х1, х3, х5.
Викладач звертається до студентів з питанням: «Друзі, що ви скажете про нашу гіпотезу? Підтвердили ми її або спростували?»
Студенти: ми переконалися у важливості вивчення теми «Похідна та її застосування». За допомогою похідної вирішуються завдання у фізиці, хімії, в економіці. Похідна використовується там, де є нерівномірне протікання процесу.
- Підведення підсумків заняття. 5 хв.
Мета. Розвиток у студентів навичок пізнавальної рефлексії як усвідомлення скоєних ними дій і розумових процесів, результатів діяльності, меж свого знання і незнання, нових пізнавальних завдань і засобів їх досягнення; контроль і оцінка процесу і результатів діяльності
Студенти підводять підсумки набраних ними балів і переводять їх у дванадцятибальну систему.
Викладач. Викладач: дівчатка і хлопці, завдяки Вашій величезній підготовчій роботі, проведено дуже цікаве заняття (оголошую оцінки і прошу студентів проаналізувати свою діяльність на занятті). Цікаво дізнатися, як ви могли б оцінити нашу спільну роботу. Пропоную зробити це так: закінчить одну з фраз, яку ви бачите на екрані.
1. Сьогодні я дізнався…
2. Було цікаво…
3. Було важко…
4. Я виконував завдання…
5. Тепер я можу…
6. Я навчився…
7. Я зміг…
8. Мені захотілося…
7. Повідомлення домашнього завдання 3 хв.
[1], Р. 3,§ 19, с.146, виконати № 702, 706, 707 с.150, підготуватись до контрольної роботи
№ 702. Тіло рухається прямолінійно за законом s(t) = 2 + 8t – t2 (шлях s – у метрах, час t — у секундах). Яку відстань пройде тіло до моменту, коли його швидкість дорівнюватиме нулю?
№ 706. Обсяг продукції V майстерні, яка виготовляє ялинкові прикраси, протягом дня виражається залежністю ![]() , де t∈[1; 8] Обчисліть продуктивність праці майстерні протягом кожної години роботи.
, де t∈[1; 8] Обчисліть продуктивність праці майстерні протягом кожної години роботи.
№ 707. Через поперечний переріз провідника в кожний момент часу t проходить заряд ![]() (q вимірюється в кулонах, а t — у секундах). Знайдіть силу струму в момент часу t = 10 с. Викладач _________________ Козлова Г.В.
(q вимірюється в кулонах, а t — у секундах). Знайдіть силу струму в момент часу t = 10 с. Викладач _________________ Козлова Г.В.
Додаток А
Веб-квест з теми «Похідна та її застосування»
Теоретики.
Мета: необхідно систематизувати теоретичні відомості про похідну
- Знайти:
- означення понять, що використовуються при вивченні теми.
- Підготувати:
- Тезаурус теми;
- Опорний конспект;
- Структурно-логічну схему системи понять.
3) Оформити звіт у вигляді слайдів презентації (електронний ресурс) і в паперовому вигляді опорний конспект.
Практики.
Мета: необхідно провести дослідження застосування теми до розв’язання прикладних задач різних галузей знань.
- Знайти:
- Приклади фізичних, економічних, біологічних, екологічних задач, розвязок яких виконується за допомогою похідної.
- Підготувати:
- Розв’язки задач з різних областей знань (див. [1]., с. 148);
- Цікаві приклади застосування похідної у повсякденному житті
3) Оформити звіт у вигляді слайдів презентації з розв’язками задач.
Історики
Мета: необхідно вивчити історію виникнення похідної.
- З’ясувати:
- Навіщо людям знадобилась похідна і хто її відкрив;
- Коли і як стала застосовуватись похідна;
- Хто з вчених застосував знак похідної «штрих», розробив таблицю похідних, хто застосовував геометричний та фізичний зміст похідної для своїх досліджень.
- Підготувати:
- Хронологію виникнення понять границі функції, похідна, кутовий коефіцієнт дотичної, фізичний та економічний зміст похідної;
- Галерею вчених, які внесли свій вклад в розвиток вивчаємої теми;
3) Оформити звіт у вигляді слайдів анімаційної презентації (електронний ресурс).
Аналітики
Мета: необхідно систематизувати та проаналізувати завдання, що були запропоновані на ЗНО з математики в попередні роки (2014-2019 роки).
- Знайти:
- Завдання, що були розглянуті на ЗНО з математики з теми «Похідна та її застосування», використовуючи сайт zno.osvita.com.ua (основна та додаткова сесії);
- Підготувати:
- Банк завдань ЗНО з математики з теми «Похідна та її застосування»,
- Пам’ятку «Зверніть увагу на …»;
- Розв’язок типових завдань з теми, що виносилися на ЗНО з математики;
3) Оформити звіт у вигляді слайдів анімаційної презентації (електронний ресурс).
Додаток Б
Лист оцінювання
Прізвище студента ______________________________________
|
№ з/п |
Зміст роботи і правила переведення правильних відповідей в бали |
Кількість отриманих балів |
|
1 |
Заповнення форми з друкованою основою Всього правильних відповідей – 14: Оцінка: 1-7 пр. відповідей – 0 б 8-11 пр. відповідей – 1 б. 12-14 пр. відповідей – 2 б. Всього 2б. |
|
|
2 |
Знайди пару Всього правильних відповідей – 11: Оцінка: 1-4пр. відповідей – 0 б 5-9 пр. відповідей – 1 б. 10-11 пр. відповідей – 2 б. Всього 2 б. |
|
|
3 |
Самостійна робота «Вправи ЗНО» Оцінювання правильних відповідей: № 1а – 0,5б. № 1б – 0,5б. № 2 – 1 б. № 3а (знаходження похідної) – 0,5б. № 3б (відповідь) – 0,5б. № 4а (знаходження похідної)– 0,5б. № 4б (відповідь) – 0,5б. Всього 4 б. |
|
|
4 |
Групова робота «Застосування похідної» Якщо група розв’язала задачу, то всі члени групи отримують: За 1 задачу – 1 б. За 2 задачу – 2 б. За 3 задачу – 1 б. Всього 4 б. |
|
|
|
Всього 12б. |
|
Додаток В
Прізвище студента:_________________________________________
Тема. Похідна та її застосування
Завдання. Заповніть картку з друкованою основою:
1. х – х0 = ______ - _____________ аргументу
2. __у = f(x0 + ___) – f(x0) - ______________функції
3. Запишіть означення похідної у вигляді формули:________________________
4. Геометричний зміст похідної: похідна – це _____________________дотичної, проведеної в заданій точці x0:______або ______________кута нахилу дотичної
5. Похідна – це __________________ швидкість – це __________________зміст похідної: ______= s(t), a (t) = _______= s(t)
6. Функція f(x) зростає на інтервалі (a; b), якщо _______________цього інтервалу ______________
7. Функція f(x) спадає на інтервалі (a; b), якщо _______________цього інтервалу ______________
8. Внутрішні точки області функції, у яких похідна дорівнює нулю, або не існує називають _________________ точками.
9. Функція f(x) є _____________на інтервалі (a; b), тоді і тільки тоді, коли
f (x) = 0 в усіх точках цього інтервалу.
10. Точки максимуму і мінімуму називають точками ___________________.
11. У точках ________________ похідна функції дорівнює нулю, або не існує.
12. Якщо функція f(x) неперервна в точці x0 і похідна f (x) змінює знак при переході через точку x0, то точка x0 – точка __________________ функції f(x).
13. Якщо неперервна функція у = f(x) має похідну, яка в точці x0 змінює знак з «+» на «– », то точка x0 – точка __________________ функції f(x).
14. Якщо неперервна функція у = f(x) має похідну, яка в точці x0 змінює знак з «– » на «+», то точка x0 – точка __________________ функції f(x).
Додаток Г
Структурно-логічна схема вивчення похідної
|
|
|
Теоретичний блок |
|
|
|
|
|
|
|
|
|
|
|
Задача про дотичну до графіка функції |
|
Поняття похідної |
|
Задача про миттєву швидкість |
|
|
|
Геометричний |
|
|
||
|
|
зміст |
зміст |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Диференціювання функцій |
|
|
|
|
Правила обчислення похідних |
|
|
Основні теореми диференціаль-ного числення |
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
Таблиця похідних |
|
|
||
|
|
|
|
|
|
|
|
Знаходження дотичної до графіка функції |
|
Застосування похідної |
|
|
|
|
|
|
Розв’язання фізичних задач |
|||
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
Розв’язання економічних задач |
|
Розв’язання рівнянь і нерівностей |
|
Дослідження функцій |
|
||
|
|
|
|
|
|
|
|
|
|
Практичний блок |
|
|
|
Додаток Д
Розв’язання вправ самостійної роботи
Виконання самостійної роботи студентами (15 хвилин):
|
№ з/п |
І варіант |
ІІ варіант |
|
1 |
а) (ЗНО 2018 основна сесія)
Укажіть похідну функції
А) Відповідь: А. |
а) (ЗНО 2018 додаткова сесія)
Укажіть похідну функції
В) Відповідь: В. |
|
|
б) (ЗНО 2017 основна сесія)
Укажіть похідну функції
Д) Відповідь: Д. |
а) (ЗНО 2015 додаткова сесія)
Якщо
Г) Відповідь: Г. |
|
2 |
(ЗНО 2015 основна сесія) Укажіть рівняння прямої, яка може бути дотичною до графіка функції у = f(x) у точці з абсцисою х0 = 2, якщо f (x) = -3. Рівняння дотичної:
Д) Відповідь: Д. |
(ЗНО 2014 основна сесія) Укажіть рівняння прямої, яка може бути дотичною до графіка функції у = f(x) у точці з абсцисою х0 = 1, якщо f(х0) = 5, f (х0) = 2: Рівняння дотичної:
Д) Відповідь: Д. |
|
3 |
(ЗНО 2016 основна сесія)
Обчисліть значення похідної функції
Відповідь: - 0,75 |
(ЗНО 2016 додаткова сесія)
Матеріальна точка рухається прямолінійно за законом
Відповідь: 41 |
|
4 |
(ЗНО 2019 основна сесія)
Знайдіть похідну функції
Відповідь: 0,5. |
(ЗНО 2017 додаткова сесія)
Знайдіть похідну функції
Відповідь: 1. |
Відповіді:
1 варіант: 1а) А 1б) Д 2) Д 3) -0,75 4) ![]() ; х1 = 0,5; х2 =-0,5
; х1 = 0,5; х2 =-0,5
2 варіант: 1а) В 1б) Г 2) Д 3) 41 4) ![]() ; k = 1.
; k = 1.
Слайди презентації
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
-
-
Дякую! Дуже гарна розробка!!!


про публікацію авторської розробки
Додати розробку

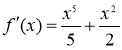
 ;
;
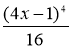 ; Г)
; Г) 




 :
: