Урок "Похідна та її застосування" (узагальнення та систематизація)

                                                                                                      Алгебра 10 клас

Тема: Похідна та її застосування

Цілі:

формування предметних компетентностей:

узагальнити, систематизувати і поглибити знання учнів з теми «Похідна та її застосування», розширити знання учнів про практичне використання похідної, формувати вміння переносити набуті знання в нові ситуації; підготувати учнів до контрольної роботи, розвивати вміння аналізувати й узагальнювати вивчений матеріал, увагу, пам’ять, мислення, кмітливість, математичну мову учнів; їх самостійну творчу діяльність. Створення комфортних умов для виховання самостійності, взаємоповаги, почуття колективізму, відповідальності, інтересу до предмету.

формування ключових компетентностей:

спілкування державною мовою- чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень;

математична компетентність – оперувати числовою інформацією;

уміння вчитися впродовж життя – аналізувати результати своєї навчальної діяльності;

соціальна та громадянська компетентності- співпрацювати в команді, виділяти та виконувати власну роль у командній роботі.

Тип уроку: узагальнення та систематизація знань.

Обладнання: комп’ютер, презентація, таблиці.

Хід уроку

І. Організаційно-психологічна частина

ПАМ’ЯТКА « 7 Я»

Епіграфом уроку будуть слова:

«Ніколи не говори: «Я-неук»,

А завжди кажи: « Я-зірка».

Але кожен з вас повинен пам’ятати:

Я-учень

Я-хочу знати

Я-думаю

Я-вмію

Я-знаю

Я-особистість творча

Я-зірка

ІІ. Мотивація навчальної діяльності учнів.  

Повідомлення теми, мети, завдань уроку.

• Діти, хто знає, що таке «бенефіс»?
• Бенефіс- це спектакль на честь одного актора або спектакль одного актора.

Сьогодні у нас урок «Бенефіс похідною»

Весь урок ми присвятимо одному математичному поняттю - похідній, побачимо, що з її допомогою вирішуються не тільки алгебраїчні завдання, але і геометричні, і фізичні.

Вступна бесіда.

У XVII ст «…в математику ввійшли рух і діалектика і… стало неминуче необхідним диференціальне та інтегральне числення».

Тема нашого уроку «Похідна та її застосування».

Прийом «Мікрофон»

• Дати означення похідної.
• Який геометричний зміст похідної.
• Які задачі призводять до означення похідної?
• Що таке критичні точки функції?
• Як знайти проміжки зростання і спадання функції?
• Навести приклади зростаючої функції, спадної функції на всій області визначення
• навести приклад функції яка у точці не має похідної.

ІІІ. Узагальнення і систематизація знань учнів

I. Теоретична розминка.

«Похідна: складно, просто, цікаво!»

Диктант.

У математиків існує своя мова - це формули. Перевіримо як ви знаєте формули. Підготуйтеся до диктанту.

І варіант

Знайдіть похідну функції:

1. .

2. .

3. .

4. .

5. .

ІІ варіант

Знайдіть похідну функції:

1. .

2. .

3. .

4. .

5. .

II. Історична довідка

Термін «похідна» є буквальним перекладом на російську французького слова «derivee», яке ввів в 1797 році Ж. Лагранж (1736- 1813); він же ввів сучасні позначення y ', f'. Таку назву відображає зміст поняття: функція f '(x) відбувається з f (x), тобто є похідним від f (x). І. Ньютон називав похідну функцію флюксіями, а саму функцію -флюентой.

   Зверніть увагу на слова А.Н. Крилова: «Теорія без практики мертва або безплідна: практика без теорії неможлива або згубна. Для теорії потрібні знання, для практики, крім того всього того, - і вміння ».

III. Практичні завдання

 А) Похідна в фізиці.

 Тіло рухається прямолінійно за законом S (t) = t3 - t. (Координати вимірюються в метрах, час - в секундах)

Визначте: 1) швидкість в момент часу t = 3 c .;

 2) прискорення руху в момент часу t = 0,2 c.

 Б) Знайдіть значення похідної в точці :

1. .

2. , .

3. , .

 В) Розв’яжіть рівняння:

1. , якщо  .
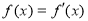2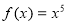. 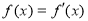, якщо  .

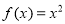Г) Таблиця-код

Варіант 1

б  ц       н   л  ей  и 

Варіант 2

ю  н  о  ь  н  т  

Відповіді (для самоперевірки):

1) [-1;2] и [5;6] л 4    5 н 1) [2;5]

2) [2;5]  ей 5    4 ь 2) [-1;2] и [5;6]

3) 2   б 1    1 ю 3) 2

4) (2;5)   н 3    6 т 4) (-1;2) и (5;6)

5) (-1;2) и (5;6) і 6    3 о 5) (2;5)

6) 5   ц 2    2 н 6) 5

ЛЕЙБНІЦ, НЬЮТОН

Д) Напишіть рівняння дотичної до графіка функції

     f (x) = х3 + х2 - 2х + 1 в точці з абсцисою х0 = -1.

     f (x) = 0,5x2-2x в точці з абсцисою х0 = 4.

 Е) Дана функція f (x) = 2х3 + 6х2- 1.

Знайдіть:

а) проміжки зростання і спадання функції;

б) найбільше і найменше значення функції на відрізку [-3; 0].

 ІV. Самостійна робота.

1. Знайдіть точки мінімуму функції f (x) = х2 - 3х.

а)0;  б) 2;   в) -2;  г) 1/5.

2. Знайдіть похідну функції y = (2х + 3) 8

  а) -16 (2х + 3) 7;    б) 24 (2х + 3) 7;

  в) 8 (2х + 3) 7;    г) -8 (2х + 3) 7.

3. Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка функції  f (x) = 9x - 4x3 в його точці з абсцисою х = 1.

  а) -3;  б) 0;   в) 3;   г) 5.

4. Знайдіть найбільше і найменше значення функції f (x) = -x3 + 2x2 - 8x+1 на відрізку [-2; 1]

ІV. Підсумок уроку

Інтерактивна вправа «Уявний мікрофон»

      Підведемо підсумки уроку. Продовжте, будь ласка, речення:

• На уроці мені знадобилися знання …
• Цікавим для мене було …
• Сьогодні я дізнався, що …
• Для мене було складно …

Сьогодні на уроці ми побачили з вами, що за допомогою Великої Похідній можна вирішувати фізичні завдання, отримувати рівняння дотичної до графіка функції, не бачачи і не будуючи цей графік

Оцінки за урок.

V. Домашнє завдання

  Повторити таблицю. похідних, геометричний зміст похідної.