Тема: Взаємообернені функції. Графіки обернених функцій

Мета :

- домогтися розуміння, яка функція може бути оборотною;  сформувати поняття оберненої функцій; домогтися засвоєння властивостей взаємно обернених функцій; навчитися виводити формулу, яка задає функцію, обернену до заданої; знаходити область визначення та множину значень функції;

– розвивати пам'ять і мислення, цікавість  до    математики, здатність до творчого застосування знань і вдосконалення умінь;

– виховувати наполегливість і відповідальність, уважність,  акуратність при побудові графіків функцій.

Тип уроку: засвоєння нових знань

Перебіг уроку

1.     Організаційний момент. Привітання, налаштування на роботу.
2.     Актуалізація опорних знань:
   • Фронтальна усна робота з класом - відповіді на теоретичні питання:

• Що називається областю визначення функції?
• Що називається областю значень функції?
• За якої умови функція парна? Непарна?
• Умова, за якої функція зростаюча; спадаюча.

За кожну правильну відповідь -1 бал.

• виконати наступні завдання у форматі ЗНО:
  1.                                                          2.                                                          3.

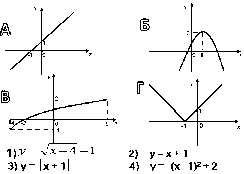
4.                                                                                      5.

Правильні відповіді (самоперевірка). Кожна правильна відповідь оцінюється в один бал-максимально 5 балів

3. Мотивація навчальної діяльності. Повідомлення теми і мети уроку.

 «Немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення»

                                                                                                     К. Ф. Лебединцев

В наші дні без функції неможливо не тільки розрахувати космічні траєкторії, роботу ядерних реакторів , біг океанської хвилі і закономірності розвитку циклону, але й економічно управляти виробництвом, організацією технологічних процесів, прогнозувати перебіг хімічних реакцій або зміну чисельності різних взаємозв’язаних в природі видів тварин та рослин, тому що все це – динамічні процеси, котрі описує функція.

На уроках математики ми вже вивчали поняття, що містять слово «обернений (на)»: обернені числа, обернена пропорційність, обернена задача, тощо. Згадайте, що означають ці поняття.

Розглядаючи різні функції, часто доводиться розв’язувати не тільки пряму задачу про знаходження за відомим значенням аргумента, а й обернену задачу про знаходження аргумента за відомим значенням функції. Наприклад, із формули , що описує функціональну залежність шляху від часу , можна знайти обернену залежність часу від пройденого шляху. Приведіть інші приклади обернених величин з фізики, математики, біології, інших галузей. (Відповіді учнів)

Тож, сьогодні ми з вами з'ясуємо, яку функцію називають оберненою, які її властивості, як побудувати її графік і як можна застосувати ці знання.

4. Усвідомлення нових знань за планом:

1. Поняття оберненої функції.
2. Властивості оберненої функції.
3. Практичний спосіб знаходження формули функції, оберненої до функції

Поняття про обернену функцію

На уроках математики ви неодноразово розв'язували задачу: обчислити значення функції у =f(x) при заданому значенніх₀аргументу. Іноді потрібно розв'язати і обернену задачу: обчислити значення аргументу х, при якому функція у =f(x) набуває даного значення у₀.

При розв'язуванні оберненої задачі виникають питання: Скільки таких значень існує? При яких умовах задача має єдиний розв'язок?

Розглянемо приклади.

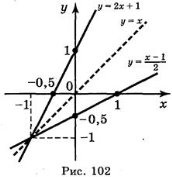
Приклад 1. Нехай задано функцію у = 2х + 1. Щоб знайти значення аргументу х, при яких функція дорівнює у₀, треба розв'я­зати рівняння у₀ = 2х + 1. Розв'язавши його

 2х = у₀ - 1;   , маємо, що для будь-якого у₀ рівняння   у₀ = 2х + 1 має і притому тільки один корінь.

Функція, яка набуває кожного свого значення в єдиній точці області визначення, називається оборотною. Таким чином, фун­кція у = 2х + 1 — оборотна, а функція у = х² (визначена на всій числовій осі) не є оборотною.

ЗАУВАЖЕННЯ

1)     Якщо функція у = f(x) задана формулою, то для знаходжен­ня оберненої функції потрібно розв'язати рівняння f(x) = у відносно х, а потім поміняти місцями х і у. Якщо рівняння f(x) = у має більше ніж один корінь, то функції, оберненої до функції 

у = f(x) не існує.

2)     Графіки даної функції і оберненої до даної симетричні віднос­но прямої     у = х.

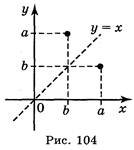Дійсно, при симетрії відносно прямої у = х вісь абсцис переходить у вісь орди­нат, а вісь ординат переходить у вісь аб­сцис, будь-яка точка (а; b) координатної площини при симетрії відносно прямої у = х переходить у точку (b; а) (рис. 104). Якщо точка (а; b) належить графіку даної функції, то точка (b; а)належить графіку оберненої функції, а ці дві точ­ки симетричні відносно прямої у = х.

3)     Якщо функція у =f(x) зростає (спадає) на деякому проміжку, то вона оборотна. Обернена функція до даної, визначена області значень функції у =f(x), також є зростаючою (спадною).

.

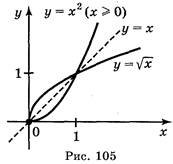Приклад 2. Функція у = х² не є оборотною в області визначення. Проте функція у = х², де х  [0; +) зростає на цьому проміжку, тому має обернену. Оберненою функцією є функція у=. Графіки цих функ­цій зображено на рис. 105.
 

Оборотні функції. Взаємно обернені функції

Розглянемо функцію y=x+4. Будь-яке значення функції y ми можемо отримати лише з одного значення змінної x. Такі функції, які набувають кожного свого значення в єдиній точці з її області визначення, називаються оборотними.

Для оборотних функцій y(x) можна знайти обернену залежність x(y), тобто знайти, яким значенням функції відповідають значення аргументу. Отримана залежність також є функцією, яка називається оберненою.

Отже, функції y=f(x) та y=g(x) називаються взаємно оберненими, якщо для кожного значення t з області визначення функції y=f(x) з рівності f(t)=m слідує, що g(m)=t.

Властивості обернених функцій:

•         Область визначення функції співпадає з областю значень оберненої, область значень функції співпадає з областю визначення оберненої (D(f(x))=E(g(x)), E(f(x))=D(g(x))).
•         Графіки взаємно обернених функції симетричні відносно прямої y=x (бісектриси І та ІІІ координатних чвертей).
•         Монотонність взаємно обернених функцій співпадає (якщо функція зростає, то обернена до неї також зростає; якщо функція спадає, то і обернена до неї функція спадає).

Як же знайти обернену функцію. Для цього достатньо виразити аргумент функції через її значення (у через х) та поміняти місцями аргумент і значення.

Приклад 1.

Знайти функцію, обернену до функції y=2x+4.

Розв'язання. Перенесемо 2х в лівий бік, а у - в правий. Отримаємо рівність -2х=4-у. Поділимо ліву та праву частину на -2. Отримаємо x= та поміняємо місцями у та х. Отримана функція y= і є оберненою.

Приклад 2.

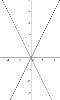
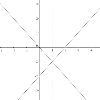
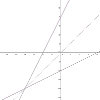
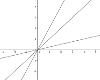
На якому малюнку зображено взаємно обернені функції.

Розв'язання. Графіки взаємно обернених функцій симетричні відносно прямої у=х, яка є бісектрисою І та ІІІ координатних чвертей. Із запропонованих малюнків пряма лише на 3 перших лінії симетричні відносно якоїсь прямої, але на першому малюнку вони симетричні відносно прямих у=0 та х=0, на другому відносно прямої х=2 і лише на третьому відносно прямої у=х. Тому правильна відповідь В.

5. Застосування набутих знань:

Робота з  підручником:

усно:  № 4.1, 4.2;

письмово: № 4.4, 4.6, 4.8, 4.11

6.   Підбиття підсумків уроку.

Дати письмові відповіді:  

1. Чи правильні твердження?

         А) Функція має обернену, якщо .

         Б) Функція має обернену, якщо .

 В) Множиною значень функції, оберненої до функції , є множина                                                                                                           дійсних  чисел.

2. Яка з наведених формул задає функцію, обернену до функції ?

  А)

  Б)

  В)

  Г) .

Послідуюча самоперевірка (за кожну правильну відповідь 1 бал). За роботу на місці протягом уроку  можна отримати максимально 10 балів. Оцінки виставляються за бажанням. Учням, які отримали не достатню, на їх думку, кількість балів, пропонується підвищити оцінку  на наступному уроці.

Рефлексія. Гарний настрій і функції

ЗАКОН ПІДЛОСТІ. Більшість дослідників дотримуються думки, що закон був відкритий  за часів Ахіллеса. ( Як гадаєте, чому?)

Закон підлості - це закон (функція) , що встановлює пряму залежність між бажанням і невдалим збігом обставин.

Тому, я вам бажаю все робити з  гарним  настроєм для отримання позитивних результатів.

7. Домашнє завдання:

Опрацювати § 4, виконати вправи № 4.5, 4.7, 4.9, 4.12*