Урок " Поняття похідної"

                                                                                                                                      Додаток

Урок 1. «Поняття похідної».

 

 

 

Тип уроку - урок вивчення нового матеріалу.

Мета уроку:

1. У предметному напрямку.

Оволодіння системою математичних знань і вмінь, необхідних для застосування у практичній діяльності, вивчення суміжних дисциплін, продовження освіти. Формування уявлень про ідеї і методи математики як універсальної мови науки і техніки, засоби моделювання явищ і процесів. Удосконалення інтелектуальних і мовленнєвих умінь шляхом збагачення математичної мови, розвитку логічного мислення. Знайомство з основними ідеями та методами математичного аналізу.

2. У метапредметному напрямку.

Виховання культури особистості, ставлення до геометрії як до частини загальнолюдської культури, формування розуміння значущості геометрії для науково-технічного прогресу.

3. У напрямку особистісного розвитку.

Формування якостей особистості, необхідних людині для повноцінного життя в сучасному суспільстві, властивих математичної діяльності: ясності і точності думки, критичності мислення, інтуїції, логічного мислення, просторових уявлень, елементів алгоритмічної культури, здатності до подолання труднощів.

Завдання уроку:

1. У предметному напрямку.

- Розглянути завдання, що призводять до поняття похідної.

- Ввести означення похідної.

- Розглянути похідні елементарних функцій.

2. У метапредметний напрямку.
3. Сформувати уявлення учнів про поняття похідної функції як про невід'ємну частину навколишнього нас світу, про використання придбаних знань і умінь в практичній діяльності. Показати учням способи опису практичної життєвої задачі математичною мовою, інтерпретувати результати вирішення завдань з урахуванням обмежень, пов'язаних з реальними властивостями розглянутих процесів і явищ. Використовувати набуті знання і вміння в практичній діяльності та повсякденному житті для дослідження (моделювання) нескладних практичних ситуацій на основі вивчених формул і властивостей фігур.
4. У напрямку особистісного розвитку.

Виховувати в учнів інтерес до математики. Формувати вміння слухати і вступати в діалог, розуміти партнера, вміти домовлятися; інтегруватися в групу однолітків і будувати продуктивну взаємодію і співробітництво з однолітками і вчителем; правильно висловлювати свої думки в мові; смислообразованіе; самовизначення; встановлення зв'язку між метою навчальної діяльності та визначенням того,                      «яке значення, сенс має ця тема для мене»; участь в колективному обговоренні проблем; планувати і узгоджено виконувати спільну діяльність, формувати адекватну самооцінку.

Навчальні матеріали уроку. 1) Алгебра і початки математичного аналізу. 11 клас. Підручник для учнів загальноосвітніх установ (профільний рівень) / Технічне оснащення: комп'ютер, презентація до уроку.

План уроку:

1. Організаційний момент.

2. Цілепокладання і мотивація.

3. Вивчення нового матеріалу (у вигляді лекції).

4. Організація первинного контролю.

5. Інформація про домашнє завдання.

6. Рефлексія (підведення підсумків уроку).

Опис основних етапів уроку.

1. Організаційний момент.

мета: створення сприятливого психологічного настрою на роботу.

Плановані результати.

Особистісні: самовизначення. Регулятивні: прогнозування своєї діяльності.

Комунікативні: вміння слухати і вступати в діалог.

Діяльність учнів: вітання, включення в діловий режим уроку. Діяльність учителя: Привітання, перевірка готовності учнів до уроку, організація уваги.

2. Цілепокладання і мотивація.

мета: забезпечення мотивації навчання учнями, прийняття ними мети уроку.

Плановані результати.

Особистісні: встановлення зв'язку між метою навчальної діяльності та визначенням того, «яке значення, сенс має ця тема для мене». Регулятивні: цілепокладання, планування, прогнозування. Комунікативні: участь в колективному обговоренні проблем; вміння чути, слухати і розуміти партнера; планувати і узгоджено виконувати спільну діяльність; вміти домовлятися; вести дискусію; правильно висловлювати свої думки в мові; поважати в спілкуванні та співпраці партнера і самого себе.Пізнавальні: самостійне дослідження, пошук, формулювання пізнавальної мети; рефлексія способів і умов дії.Логічні: підведення до поняття; побудова логічного ланцюга міркувань; висування гіпотез і їх обгрунтування.

Оголошення теми уроку. Спільна постановка мети уроку.

Фронтальна бесіда з класом.

На попередніх уроках ми ввели поняття «приріст аргументу» і «приріст функції», навчилися знаходити відношення приросту функції до приросту аргументу, а також границю цього відношення за умови, що Δx

Ці поняття допоможуть нам розглянути завдання, які приведуть нас до дуже важливого в математиці це - поняттю «похідною».

3. Вивчення нової теми (у вигляді лекції).

Мета : розгляд завдань, що приводять до поняття похідної; введення означення похідної; знаходження похідних елементарних функцій за означенням.

Плановані результати.

Пізнавальні: структурування знань, усвідомлення і виробництво мовного висловлювання, побудова моделі - перетворення об'єкта з чуттєвої форми до знаково-символічної, перетворення моделі з метою виділення загальних законів. Регулятивні: контроль у формі звірення дії і його результату за заданим еталоном з метою виявлення відхилень і відмінностей від еталону, передбачення результату і рівня засвоєння знань, його тимчасових характеристик. Комунікативні: вміння слухати і вступати в діалог; інтегруватися в групу однолітків і будувати продуктивну взаємодію і співпрацю з учителем; правильно висловлювати свої думки в мові. Особистісні: смислоутворення.

Пояснення вчителем нового матеріалу (супроводжується презентацією).

 

I. Завдання, що призводять до поняття похідної.

Завдання про швидкість руху.

Розглянемо прямолінійний рух деякого тіла. Закон руху заданий формулою                                         S = S (t), тобто кожному моменту часу t відповідає певне значення пройденого шляху S. Знайти швидкість руху тіла в момент часу t.

Розв’язання: нехай в момент часу t тіло знаходиться в точці М.

Надамо аргументу t прирощення Δt, за цей час тіло переміститься в деяку точку Р-пройде шлях ΔS.

Отже, за час Δt тіло пройшло шлях ΔS.

Що можна знайти, знаючи ці два значення?

, маємо середню швидкість руху тіла за проміжок часу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Означення: Середньою швидкістю руху тіла називається відношення пройденого шляху до часу, за який цей шлях пройдено.

У фізиці часто йде мова про швидкість v (t), тобто швидкості в певний момент часу t, часто її називаютьмиттєвою швидкістю.

Можна міркувати так: миттєву швидкість отримаємо якщо Δt, тобто Δt вибирається все менше і менше, тобто

 

 

Можна вказати ще багато завдань з фізики, геометрії (підручник, стор.157 - 159), для вирішення яких необхідно відшукати швидкість зміни відповідної функції.

Наприклад, відшукання кутової швидкості тіла, що обертається, відшукання теплоємності тіла при нагріванні, лінійний коефіцієнт розширення тіл при нагріванні, швидкість хімічної реакції в даний момент часу і т.п.

Всі ці завдання вимагають для свого рішення знаходження швидкості зміни відповідної функції.

Через велику кількість завдань, що призводять до обчислення швидкості зміни функції або, інакше, до обчислення межі відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля, виявилося необхідним виділити таку межу для довільної функції і вивчити його основні властивості.

Ця межа називається похідною функції.

II. Визначення похідної.

визначення: Похідною функції y = f (x) в даній точці x0 називається границя відношення приросту функції в цій точці до приросту аргументу, за умови, що приріст аргументу прямує до нуля.

Позначення похідної:. тоді або

 

 

 

Якщо уважно проаналізувати визначення похідної, то ми виявимо, що в ньому закладено алгоритм знаходження її.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

За допомогою цього алгоритму можна знайти похідну будь-якої функції, тобто отримати таблицю похідних, а також довести правила обчислення похідних, якими надалі ми і будемо користуватися.

4. Організація первинного контролю.

Перший приклад вчитель розглядає спільно з учнями з оформленням рішення на дошці і зразком записи в зошиті. Всі наступні приклади вирішуються учнями або самостійно з подальшою перевіркою, або роботою в групах (учитель - консультант), або один учень виконує роботу на дошці, інші ведуть запис рішення в зошиті.

Приклад 1.

Знайти похідну функції y = C.

Рішення: f (x) = C.

1.Рассмотрім два значення аргументу x і x + Δx.

2.

3.

4.Значіт, = 0 або похідна постійної дорівнює нулю.

 

Приклад 2.

Знайти похідну функції y = x.

Рішення: f (x) = x.

1.Рассмотрім два значення аргументу x і x + Δx.

2.

3.

4.іт, = 1.

 

Приклад 3.

Знайти похідну функції y = x2.

Рішення: f (x) = x2.

1.Рассмотрім два значення аргументу x і x + Δx.

2.

3.

4 ..

Значить, = 2x.

 

Приклад 4.

Знайти похідну функції y =.

Рішення: f (x) =.

1.Рассмотрім два значення аргументу x і x + Δx.

2.

3.

4 ..

Значить, = k.

 

Приклад 5.

Знайти похідну функції y =.

Рішення: f (x) =.

1.Рассмотрім два значення аргументу x і x + Δx.

2.

3.

4 ..

Значить, =.

 

Приклад 6.

Знайти похідну функції y =.

Рішення: f (x) =.

1.Рассмотрім два значення аргументу x і x + Δx.

2.

3.

4.

 

Помножимо чисельник і знаменник дробу на вираз, поєднане чисельнику

 

 

 

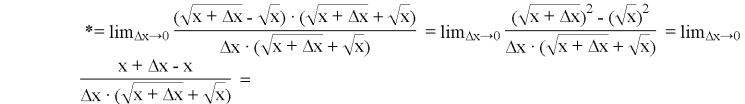
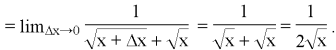
Значить, =.

 

Таким чином, за допомогою визначення похідної, можна знайти похідну будь-якої функції.

Запишемо знайдені похідні в таблицю і надалі будемо їй користуватися.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

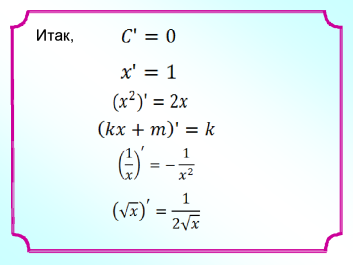
5. Інформація про домашнє завдання.

мета: забезпечення розуміння учнями цілей і змісту домашнього завдання.

Плановані результати.

Пізнавальні: пошук і виділення інформації.

6. Рефлексія (підведення підсумків уроку).

мета:якісна оцінка роботи класу і окремих учнів. Організувати рефлексію учнів з приводу їх психологічного стану, мотивації власної діяльності і взаємодії з оточуючими.

Плановані результати.

регулятивні: Оцінка - усвідомлення рівня і якості засвоєння матеріалу; контроль. Особистісні: морально-етичне оцінювання, смислообразованіе. Комунікативні: вміння з достатньою повнотою і точністю виражати свої думки. Пізнавальні: рефлексія способів і умов дії.