Співвідношення між тригонометричними функціями числового аргументу

Урок №                           дата______   10 клас

 

Тема уроку: Співвідношення між тригонометричними функціями числового аргументу

Мета уроку: Навчальна: вдосконалити знання учнів з теми; сформувати вміння виконувати перетворення виразів, використовуючи основні співвідношення тригонометричних функцій одного аргументу.

Розвиваюча: розвивати математичну мову та логічне мислення учнів; розширювати кругозір учнів.

  Виховна: виховувати колективізм, почуття відповідальності за      доручену справу.

Очікувані результати: учні повинні знати основну тотожність і наслідки з неї та використовувати ці знання при розв’язанні прикладів та висловлювати власні думки.

Обладнання: підручники, дидактичний матеріал, комп’ютерні технології.

Тип уроку: удосконалення вмінь та навичок учнів.

Вид уроку: урок з елементами інтеграції.

 

Хід уроку

 

І. Організаційний момент (1 хв.)

       Оголошення теми й мети уроку.

Сьогодні, на уроці ми з вами  повторимо тригонометричні функції, формули співвідношення тригонометричних функцій числового аргументу та пригадаємо, як вони використовуються при розв’язанні різних вправ.

ІІ. Перевірка домашнього завдання                      

1. Перевірити наявність домашнього завдання.    

ІІІ. Мотивація навчання

Розповідь учителя

Девізом  уроку  є слова видатного  українського  математика,  названого  академіком  М.М.Боголюбовим  «найталановитішим  алгебраїстом  XX  століття»,  М.П.Кравчука: «Не опускайте рук, займайтеся математикою, і ви прозрієте душею».

Я теж закликаю вас під час уроку бути максимально уважними та активно  працювати. 

 А для цього потрібно налаштуватися. Почнемо із завдання на увагу. Дивимося і запам’ятовуємо.

 

     

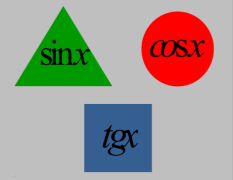
 1. Перерахуйте всі тригонометричні функції, які ви запам’ятали. 

  2. В якій геометричній фігурі розміщений вираз сosx?

            3. Якого кольору це коло?

          4. Яка функція знаходиться в середині квадрата?

          5. Якого кольору цей квадрат?

          6. Яка тригонометрична функція розташована в середині трикутника?

          7. Якого кольору цей трикутник?

IV. Актуалізація опорних знань

     Теоретична розминка

Графічний диктант

1. Чи вірно ,що косинус парна функція?
2. Чи правильно , що кут 390⁰  - кут ІІ чверті?
3. Чи вірно ,що період тангенса 2п ?
4. Чи вірно ,що відношення ординати точки до радіуса одиничного кола називається косинусом?
5. Відомо , що sin a  і cos a є від’ємними . Чи може кут а бути кутом ІV чверті?
6. Чи вірно ,що відношення протилежного катета до прилеглого катета називається тангенсом?           +,- ,- ,-,-,+

 

V.  Узагальнення  і систематизація  умінь і навичок  учнів щодо розв’язування вправ на перетворення тригонометричних виразів

Тригонометрія! Як багато ми про неї знаємо? Яка ж історія її виникнення? Якими історичними пам’ятками володіє? І головне – це те, де саме ми можемо її зустріти у повсякденному житті? Думаю, на усі ці питання ми знайдемо відповідь переглянувши презентацію.

 1. Перегляд презентації  ( слайд 5-9)

“Тригонометрія”(від грецьких слів “тригонон”–трикутник і “метріо”-вимірюю) означає “вимірювання трикутників”. Виникнення тригонометрії пов'язане з розвитком астрономії, зародилась та розвивалась у Вавилоні, Єгипті, Китаї, Індії та інших древніх країнах.

 Тригонометрія виникла із практичних потреб людини. З її допомогою можна визначити відстань до недоступних предметів й, взагалі, істотно спрощувати процес геодезичної зйомки місцевості для складання географічних карт. Тригонометричні функції широко застосовуються в математиці, фізиці, техніці. Багато процесів, такі як коливання струни, маятника, звукові коливання, напруга в ланцюзі змінного  струму описується за допомогою тригонометричних функцій

Леонард  Єйлер – видатний швейцарський математик.

Саме він ввів більшість математичних понять та символів у сучасну математику, наприклад: f(x), e, π (пі), уявна одиниця i, символ суми ∑ , знак             і багато інших;

увів означення сучасних тригонометричних функцій, вивів формули зведення

 

Рух риб у воді відбувається за законом синуса або косинуса, якщо зафіксувати точку на хвості, а потім розглянути траєкторію руху.

Під час плавання тіло риби набуває форми кривої, яка нагадує графік функції у = tg x.

 

 

 

 

 

2.Розвязування вправ біля дошки по рівнях

 

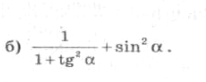Середній рівень

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

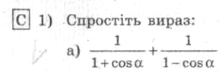
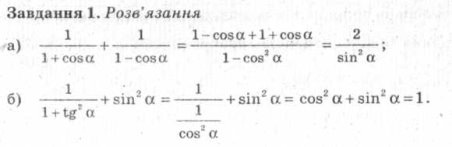
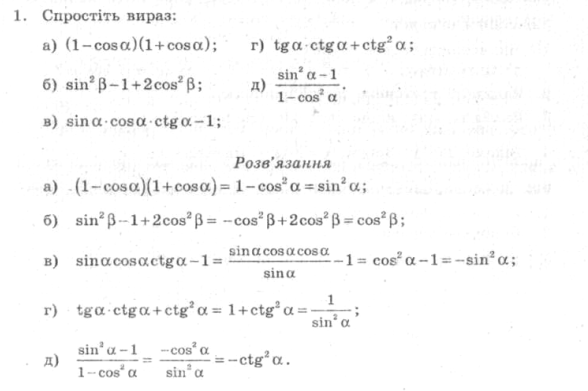
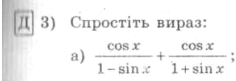
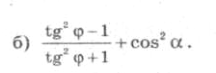
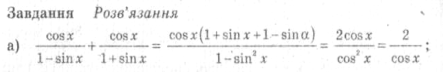
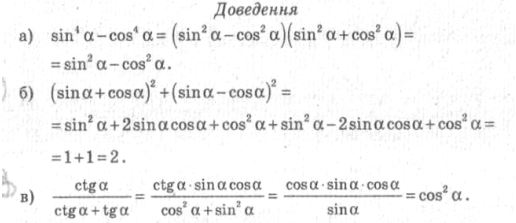
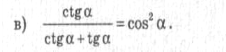
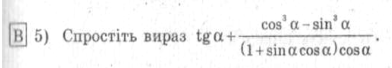
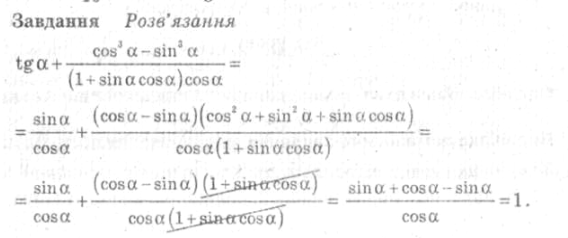
3.Поетична хвилинка

 

Косинус мій, чому ти не синус?

Я б за знак функції винесла мінус

Чому ти не тангенс,що швидко зростає,

До нескінченності з прірви сягає?

 

Косинус, графік я твій намалюю,

В кольори різні його розфарбую,

В класі його почеплю на стіні-

Іншим на смуток, на втіху мені.

 

Ряд коливань, наче хвилі на морі...

Учням не суть вони розпач і горе.

Точок китичних там дуже багато,

Важко їх навіть усі пригадати.

 

То він зростає, а то він спадає,

Модуля більш одиниці не має.

Має проте він багато нулів,

Всіх їх назнавати не вистачить слів.

Діти чи знаєте ви до , якого лікаря треба звернутись коли у людини болить  синус?

1.Якщо болять зуби, ми звертаємось до стоматолога, якщо болить серце – до кардіолога. А до якого лікаря треба звернутись, якщо болить синус?

Відповідь: До отоларинголога (вухо-горло-ніс). У носовій порожнині людини є западинки-синуси, їх запалення називається синуситом.

Інший варіант відповіді: у головному мозку теж є западинки-синуси.

 

 

 

3. Самостійна робота (7 хв.)

      І варіант       ІІ варіант

1) спростити вираз:     

 

а) (1 – cos²ℒ): cos²ℒ;     а) (1 – sin²ℒ): sin²ℒ;

б) (1 – cos²ℒ)(1 + tg²ℒ);    б) (1 – sin²ℒ)(1 + ctg²ℒ);

 

2) Доведіть тотожність:

  І варіант       ІІ варіант

tg²ℒ - sin²ℒ = tg²ℒ sin²ℒ;         ctg²ℒ - cos²ℒ = ctg²ℒ cos²ℒ;

 

 

 

VІ.підведеня підсумків.

VІІ. Домашнє завдання (1 хв.)

 

 

Створити презентацію на тему «Тригонометрія в різних науках»