Опорний конспект "Формули зведення"
Опорний конспект з алгебри
( 10 клас , рівень стандарт )
з теми « Формули зведення»
Формули зведення – це формули перетворення тригонометричних функцій кута, за допомогою яких тригонометричні функції від аргументів виду πk 
α і (2k+1)
α , де k∈Z , зводяться до тригонометричних функцій від аргумента α.
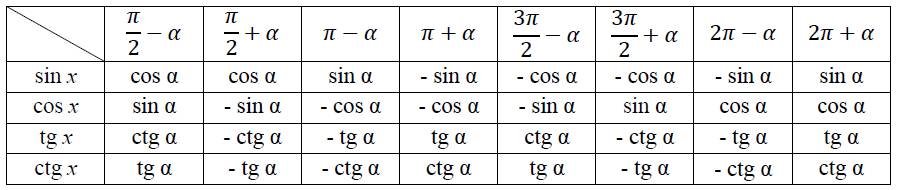
Щоб використовувати цю таблицю, необхідно мати гарну пам’ять. Тому для спрощення тригонометричних функцій від аргументів виду πk α і (2k+1) α , де k∈Z , пропонуємо наступний алгоритм.
Алгоритм використання формул зведення
- Якщо кут отриманий відхиленням на α від горизонтального діаметра (одиничного кола), то назва заданої
функції не змінюється.
- Якщо кут отриманий відхиленням на α від вертикального діаметра (одиничного кола), то назва заданої функції змінюється на конфункцію ( синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
- Знак отриманого виразу визначається знаком початкової функції ( кут α умовно вважаємо гострим).
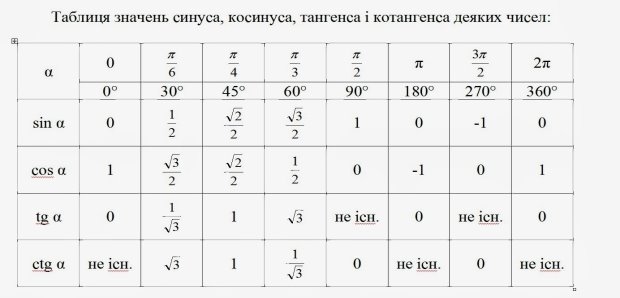
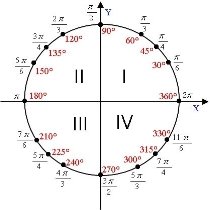
Повторимо опорні факти :
1.
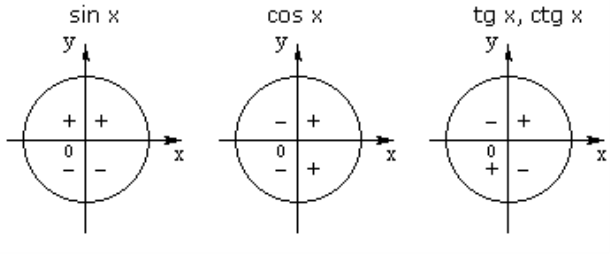
2. Знаки тригонометричних функцій за чвертями:
Приклади розв’язування вправ:
Розв’язання:
Відповідь : |
|
Розв’язання:
Відповідь : |
|
Розв’язання:
знак «+»
Відповідь :
|
|
Розв’язання:
Відповідь :
|
|
Розв’язання:
Відповідь :
|
|
Розв’язання:
Відповідь :
|
|
Розв’язання:
знак «+»
Відповідь :
|
|
|
8.Спростити вираз Розв’язання:
Відповідь : |
|
- 
+ 
- 
- 
+ 
- 
5π + 
Приклади застосування формул зведення.
|
Приклади |
Розв’язання
|
|
1 . Знайти значення виразу:
А)
Б)
В)
Г)
|
Розв’язання :
А)
Б)
В)
Г)
|
|
2. Спростити вираз:
А)
Б)
|
Розв’язання :
А)
Б)
= |
-
-
Чудово розписано! Набагато легше розуміється матеріал!
-
про публікацію авторської розробки
Додати розробку