Урок "Повторення формул скороченого множення"

 

 

 

 

 

 

 

 

 

 

 

 

Відкритий урок на тему:

 

ПОВТОРЕННЯ

ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Підготувала вчитель математики

Поддубна Юлія Володимирівна

 

Тема уроку. ПОВТОРЕННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ.

Мета уроку:    

                          – навчальна

формувати, удосконалити та поглибити знання та вміння учнів використовувати формули скороченого множення: , при розв’язуванні вправ;

–        розвивальна

розвивати логічне мислення, математичну мову, вміння чітко висловлювати думки, узагальнювати, активність;

–        виховна

інтерес до математики.

Тип уроку: урок-подорож (застосування знань умінь навичок).

Обладнання: роздатковий матеріал, картки з відповідями, картки самоконтролю. Презентація Power Point.

Форми роботи: колективна, індивідуальна.

 

ХІД УРОКУ

 

Девіз уроку: «Найкращий спосіб вивчити що-небудь – це відкрити самому» (Д . Пойа, угорський, швейцарський, американський математик)

 

І. ОРГАНІЗАЦІЙНА ЧАСТИНА

 

ІІ. ПОВІДОМЛЕННЯ ТЕМИ І МЕТИ УРОКУ

Добрий день! Сідайте. Я рада сьогодні бачити ваші допитливі очі, чути ваші правильні відповіді. Сьогодні на 45 хвилин ми поринемо у чудовий, незвичайний світ науки, яка зачаровує, дивує, манить. Науки, яка оточена містикою, магією. Звісно, це  –  математика.

Першим поштовхом до пізнання видатний грецький філософ Арістотель вважав здивування. Для первісної людини здивувань було надто багато, але минав час, проходили епохи, набувався досвід, здивувань меншало, з’являлись люди, які на дозвіллі могли цілеспрямовано займатися спогляданням. Це були жерці при культових храмах. Вони першими помічали закономірності, пов’язані зі зміною дня і ночі, фаз Місяця, положення сузір’їв на  небі. Фіксація цих закономірностей потребувала відповідної цифрової символіки. Їм зазвичай давались міфічні пояснення. Так з’явилась числова містика.

І ось вже від початку навчального року ми з вами подорожуємо містами нової для вас країни Алгебри. Нещодавно ми дісталися ще одного міста – ФСМ, що означає Формули скороченого множення.

Сьогодні ми пройдемося вулицями цього міста, щоб дізнатися, що тут є цікавого і незвичайного.

Працювати ми будемо над темою «Повторення формул скороченого множення».

 У кожного з вас на парті лежать картки самооцінювання. Сьогодні ми будемо працювати на довірі. Оцінювати себе ви будете самі.

ІІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

Для  подорожі містом, нам слід бути впевненими, настільки добре  ми до неї підготувались.

Звірте з дошкою правильність розв’язання домашнього завдання та оцініть його.             

    1)   (х+3)²=х²+6х+9;   

    2) (a²-c)²=a⁴-2a²c+c²;    

    3)  (ax+b²)²=a²x²+2axb²+b⁴;      

    4) (-1+2c³)²=4c⁶-4c³+1;    

    5)   12ab-(2a+3b)²=12ab-4a²-12ab-9b²= -4a²-9b²;    

    6)  (х-3)² =(х-5)(х+4);                          

         х²-6х+9=х²+4х-5х-20;                        

        -6х-4х+5х= -20-9;                               

        -5х= -29;                                             

              х= 5,8.  

                                              

ІV. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Щоб зайти в місто я повинна бути впевнена, що ви бадьорі і сповнені сил

     Графічний тренінг

Якщо вираз записано правильно, то учні ставлять в зошиті ˄, а якщо не правильно, то _

Вправа «Знайди помилку»

1. (b-y)²=b²-2by+y²
2. (3a+5b)²=9a²+30ab+25b²
3. (3п-2р)²=3п²-12пр+2р²
4. (2a+1)²=4a²+4a+1
5. 49-c²=(49-c)(49+c)
6. (p-10)²=p²-20p+100
7. (2а-с)(2а+с)=4а²-с²

 (Правильний запис ˄˄_˄_ ˄˄)

На що схожі ваші записи? На кардіограму. Отже, ваша кардіограма вказує на те, що настій у вас гарний і ви готові відвідати наше місто ФСМ.

 

Але для успішної подорожі містом нам потрібно придбати перепустки, які ви отримали на попередніх уроках.

Давайте разом пригадаємо з вами основні формули скороченого множення

- квадрат суми двох виразів

- квадрат різниці двох виразів

a²-b²=(a-b)a+b)- різниця квадратів двох виразів

 

  Гра «Дивись, не помились!».

На дошці записані завдання. Потрібно відновити записи – вставити пропущені символи.

 

Завдання. Відновіть записи:

1. (a+b)²=a²+2ab+…
2. (m-…)²=m²-2mn+n²
3. (…+y)²=…+2xy+y²
4. (a²…b)²=…-2a²b+b²
5. (3-y)²=9…6y…y²
6. (3x+2y)(3x-…)=9x²-4y²
7. (6x-…)²=36x²-…+1

 

Отже, сьогодні ми будемо працювати над повторенням формул скороченого множення, і дізнаємось, де їх можна використовувати.

 

V. ІСТОРИЧНА ДОВІДКА

Ось ми уже в місті ФСМ. І одразу ж потрапили на станцію «Історичну». Розгляньте уважно рисунок.

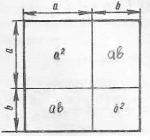          Формули скороченого множення, які ми зараз вивчаємо, античні математики використовували задовго до нашої ери. На той час формули подавалися не у звичному нам символічному вигляді, а формулювалися словами.

 Учені Давньої Греції алгебраїчні твердження, формули, що виражають певні залежності між величинами, трактували геометрично. Так, добуток вони розглядали як площу прямокутника зі сторонами та .

 Подивимося з вами на приклад алгебраїчного твердження, яке було відомим давньогрецьким ученим, і яке в геометричній термінології формулювалося так:

Площа квадрата, побудованого на сумі двох відрізків, дорівнює сумі площ квадратів, побудованих на кожному з цих відрізків, плюс подвоєна площа прямокутника, побудованого на цих відрізках. Як ви вважаєте, про яку формулу скорочено множення йдеться мова?

 Мова йдеться про формулу квадрата суми, яку ми символічно записуємо так:

.

Давньогрецький учений Евклід (3 ст. до н. е.), який створив посібник з математики «Начала», першим геометрично вивів формулу квадрата двочлена (буквенна символіка була введена пізніше у XVI-XVII ст.)

 

VІ.  ФІЗКУЛЬТХВИЛИНКА

Не можна пройти повз   вулиці «Спортивної». Погляньте як тут цікаво!  Давайте і ми з вами приєднаємося до жителів цієї вулиці.

 

     VІІ. РОЗВ’ЯЗУВАННЯ ВПРАВ НА ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ

Продовжуємо свою подорож. І ось вулиця «Рахувати-Хитрувати». Завітаємо сюди.

    Застосування формул скороченого множення для виконання обчислень (швидкої лічби).

1.   За допомогою якої формули  скороченого множення легко обчислити значення

 99·101

 99·101=(100-1)(100+1)=100² - 1=9999

 

Показати учням кілька прикладів знаходження квадратів двоцифрових чисел, що закінчуються цифрою 5.

Наприклад, 25²=625; 35²=1225; 75²=5625 і. т. д.

 

2. Обчислити: 57·53.

Розв’язання:

 

    Застосування формул скороченого множення для піднесення довільного многочлена до квадрата.

Наша подорож триває. Ми дістались вулиці «Дослідників». Давайте заглянемо, що тут відбувається.

Перейдемо до одного узагальнення, початок якому поклали стародавні вавілоняни.

 Ви знаєте тотожність (a+b)²=a²+2ab+b².

Запропонуйте спосіб піднесення двочлена до кубу.  (a+b)³=(a+b)²(a+b)=(a²+2ab+b²)(a+b)=a³+a²b+2a²b+ab²+b³=

=a³+3a²b+3ab²+b³.

Що ви можете сказати за показники числа а? (спадають); числа b? (зростають).

А якщо піднесемо двочлен до четвертого степеня, які будуть показники степенів? (Розписати без коефіцієнтів:

(a+b)⁴=   a⁴+  a³b+   a²b²+   ab³+   b⁴

 Чого не вистачає в цій формулі? (Коефіцієнтів.) Спробуємо знайти їх за допомогою незвичайного трикутника.

 Можна побачити, що “сторони” цього трикутника складені із одиниць, а числам, які стоять всередині  трикутника, притаманна властивість. Яка? (Кожне число можна подати у вигляді суми чисел, які стоять над ним у попередньому ряду праворуч і ліворуч:

Спробуйте дописати наступні рядки і  виправити формулу четвертого степеня двочлена:

(a+b)⁴ =a⁴+4a³b+6a²b²+4ab³+b⁴.

 Піднесіть двочлен до п’ятого степеня, використовуючи вказані властивості: 

(a+b)⁵ =a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵.

 Трикутник, складений за вказаним правилом, називають трикутником Паскаля, названим ім’ям відомого математика, фізика, філософа, письменника Блеза Паскаля (1623 - 1662), сучасника Декарта і Ферма.

 Де ви чули це прізвище?

-         На уроках фізики: тиск вимірюється в паскалях.

-         На уроках інформатики: існує мова програмування  Паскаль.

Це була дивовижна людина. 12-річним хлопчиком він доводить неймовірний факт: у будь-якому трикутнику сума всіх трьох кутів разом складає два прямі кути (зараз ми сказали б 180^о). У 16 років він здійснив справжнє наукове дослідження: відкрив нові властивості конічних перерізів. У 23 роки він завершив виснажливу роботу над першою в світі арифметичною машиною, за допомогою якої можна було виконувати дію додавання та віднімання. Саме завдяки цьому в інформатиці одна з мов програмування названа його іменем. А крім цього роботи з фізики, комбінаторики, філософські роздуми та багато іншого.

 Отже, яким чином ми узагальнили формулу квадрата двочлена?

(Навчились підносити двочлен до будь-якого натурального степеня)

 

     Застосування формул скороченого множення для спрощення і перетворення виразів.

Продовжуємо свою подорож. І ось ми дісталися «Вулиці письменників». Які цікавинки нас чекають тут?

Математичне лото

Відповіді знаходяться на зворотному боці карток, де записані завдання. При правильному виконанні учні мають отримати  вислів М. Горького: «Немає сили могутнішої за знання; людина, озброєна знаннями, - непереможна».

Спростіть вираз:

Робота в парах:

1.     (5х-3)(5х+3)-25х²
2.     (а-5)²-а(а-10)
3.     (х+4)²+(х+1)(х-9)
4.     (х-1)²-(х-2)²
5.     (3х+2)²+(3х-2)²
6.     (х-2)²-(х-3)(х+3)

 

     Застосування формул скороченого множення для розв’язування рівнянь.

І наша подорож закінчується відвідуванням будинку, де проживає «Містер Х»

1.     2х(8х-5)-(4х+1)²=35 – з поясненням біля дошки
2.     х(х-2)-(х+5)²=-1 – самостійно.

 

КВИТОК ДОДОМУ.  Знайдіть у правій колонці відповіді до прикладів у лівій колонці.

1.                                                                       1.

2.                                                               2.

3.                                                                  3.

4.                                                                       4.

5.                                                                    5.

6.                                                             6.

 

Правильні відповіді
        1 - 5
        2 - 6
        3 - 1
        4 - 3
        5 - 2
        6 - 4

 

VІІІ. ПІДСУМКИ УРОКУ

     Учні ставлять собі оцінку за урок і здають картки самооцінювання.

     Вчитель дякує за урок.

Я сподіваюсь, що вам сподобалася подорож містом ФСМ і ви відкрили для себе щось нове і цікаве; ви переконалися, що знання формул є досить важливим, оскільки набагато скорочує нашу роботу, а також допомагає при розв’язуванні нестандартних завдань і навіть завдань олімпіадного типу. І цим самим наші сили після цього уроку зміцніли. Тож, я бажаю вам набиратися сил з великою швидкістю, щоб у майбутньому стати непереможними!

 

ІХ. Домашнє завдання

Повторити ФСМ, розв’язати №576(2), №788 за підручником О.С.Істера. Алгебра, 7 клас