Урок "Правильні і неправильні дроби"

Мета уроку: формувати поняття «правильний дріб», «неправильний дріб»,
вміння розрізняти правильні і неправильні дроби, застосовувати правило порівняння дробів із однаковими знаменниками і розв'язувати задачі;
встановити правила порівняння дробів з однаковими знаменниками;
виховувати інтерес до математики, історії математики;
показати безпосередній зв'язок математичних понять з оточуючим світом.
План уроку
І.Організаційний етап
ІІ. Актуалізація опорних знань
1. Мотивація навчальної діяльності. Перевірка домашнього завдання.
2. Робота в групах. «Калейдоскоп знань»
ІІІ. Основний етап.
1. Вивчення нового матеріалу.
2. Закріплення вивченого матеріалу.
3. Практичне закріплення нового матеріалу
Фізкультхвилинка
ІV. Заключний етап.
1. Гра «Реальність часу»
2. Домашнє завдання:
3. Рефлексія
4. Підсумок уроку. Оцінювання учнів.
5. Заключне слово вчителя
. Хід уроку
І.Організаційний етап
ІІ. Актуалізація опорних знань
Перевірка домашнього завдання.
Учні обмінюються зошитами в парах і виконують взаємоперевірку, роблять помітки де виконано невірно, оцінюють разом зі мною. (№ 992, № 994)
Правильне розв’язування записане на дошці.
Мотивація навчальної діяльності учнів.
Для свідомого сприйняття учнями понять проводжу бесіду при наявності наочного матеріалу – різаних яблук. Учні бачать частини і записують їх кількість дробами. При підрахунку і записі чвертей, учні використовують звичайні їм дроби і дроби у яких чисельник більший знаменника - неправильні дроби. Це створює ситуацію інтересу, що стимулює їх до дальшої навчальної діяльності. На столі 4 яблука. Одне із них поділено на дві рівні частини, друге – на три, третє і четверте – на чотири.
Використовуючи метод «ключових» запитань, пропоную розглянути дані запитання з різних точок зору.
- Половина, третина, чверть . Це частини яких яблук?
- Чи можна записати такі частини натуральними числами?
- Якими дробами можна записати ці частини?
- На що вказує чисельник, знаменник дробів?
- Три чверті, чотири чверті, шість чвертей – записати дроби на дошці.
- Що необхідно зробити, щоб мати одинадцять четвертих яблука?![]()
- Чи можуть з’їсти гості на день народженні ![]()
![]() святкового торта? Чи може Працелюб виконати
святкового торта? Чи може Працелюб виконати ![]() норми?
норми?
Формулюється мета уроку.
«Калейдоскоп знань»
Вивчаючи тему «Звичайні дроби», ви збирали про них історичні матеріали, вірші, казки, малювали. Настав час повідомити іншим про свої здобутки.
Повідомлення учнів І групи «Математика на поетичній орбіті»
Учень1.
Для вивчення цих чисел
Вагомі є причини:
Вимірювати треба
Нам різні величини.
У прикладах, задачах
Ділити без остачі —
Допомогти готові
Тут числа нам дробові.
Учень 2.
У країні числовій є чарівні числа.
Ось одне із них - це дріб,
Риска — це намисто,
А чисельник — голова,
А знаменник — ноги.
Ось картина вам жива: Красені ці дроби.
Учень 3.
В математиці є дроби. І всі вони цікаві,
Як стають вони в рядок, то ідуть у свій танок!
З ними можна танцювати, їх лиш треба добре знати
Повідомлення учнів ІІ групи «Мандрівники в минуле ».
Наша група повинна була дізнатися про історію виникнення дробів. Тому ми вирушили в бібліотеку і дізналися про таке:
Учень1.
3 виникненням уявлень про цілі числа виникли уявлення і про частини одиниці. Першим дробом, з яким ознайомилося людство, було позначення половини якого-небудь реального предмета - 1/2.Є всі підстави припускати, що спочатку існували тільки дроби із числом 2 у знаменнику. Пізніше до них було приєднано дріб -1/3.
Учень 2.
У стародавньому Єгипті дробами оперували ще 4 тисячі років тому. Проте загальної форми запису дробів, як це прийнято нині у єгиптян не було. Запис дробу за допомогою дробової риски став відомим вже в 16 столітті.
Учень 3.
Римляни користувалися конкретними дробами. Вони зосередили свою увагу на аптекарський фунт. Аптекарський фунт ділився на 12 частин —унцій. З них складали всі дроби із знаменником 12
Учень 4.
Вавілоняни користувалися дробами із знаменником 60, які називали шістдесятковими дробами. Саме з ними пов'язаний сучасний поділ години на 60 хвилин (1год = 60 с), а хвилини на 60 секунд (1 хв = 60 с).
Учень 5.
Сучасне позначення дробів бере початок у стародавній Індії. Його використовували араби, а потім у XII—XIV ст. запозичили європейці. Спочатку дроби записували без дробової риски; пізніше дробову частину стали писати чорним чорнилом або відділяти вертикальною рискою. Риску дробу почали застосовувати близько 300 років тому.
Учень 6.
У Європі сучасний запис дробів у 1200 році ввів італієць Фібоначчі. Він першим ужив термін «дріб». Назви «чисельник» і «знаменник» у XIII ст. зустрічаються у грецького математика Максима Плануда.
Вчитель:
Дроби виникли в глибоку давнину, задовго до грецької цивілізації, точної дати часописи не містять.
Хронологія така:
в слов'янській мові слово дріб з'явилось у VIII ст., походило від слів "дрібнити", "ламати", "розбивати";
риску дробу почали використовувати 300 років тому;
сучасний запис дробу розповсюдив італійський купець Фібоначчі у 1202 р., він же ввів термін "Дріб";
терміни "чисельник", "знаменник" – у ХІІІ ст. Максим Плануд – грецький монах, учений математик.
Повідомлення учнів ІІІ групи «Журналісти»
Земля і дроби.
3/4 – покрито водою
1/4 – суша
1/8 – поверхня Землі на якій можна жити
1/8 - пустелі, гори, ліси,
3/32 – місця, де можуть жити люди
1/32 – поля, де вирощують врожай.
Уявіть собі, що яблуко – це наша Земля. Розріжте його на частинки і ви побачите, яка мала частина Землі придатна для життя людини.
Тож, бережіть її!
ІІІ. Основний етап.
1. Вивчення нового матеріалу.
В будинку живе Вінні Пух зі своїми друзями. Для знайомства з ним нам потрібно розв’язати нескладні задачі
1). На день народження Ослик спік пиріг, який порівну поділив між десятьма запрошеними. Але Пʼятачок зателефонував, повідомивши, що приїхати не зможе.
- Яку частину пирога отримав кожний з дев'яти прибулих гостей?
Обери правильну відповідь:
А) Кожний отримав частину 1/10; 1/8; 1/4;
- Яка частина залишилась на долю Пʼятачка?
Обери правильну відповідь:
Б) залишилась частина 1/6; 1/4; 1/10,
- Яку частину пирога з'їли всі присутні, якщо ніхто не відмовився і не просив добавки?
Обери правильну відповідь:
В) з'їли 9/10; 5/6; 9/8 частин.
2). На день народження Ослик спік два однакових пирога, обидва поділила порівну на 10 рівних частин за кількістю запрошених. Гості з'їли по одному шматочку, а потім двоє з них попросили по одному шматочку від другого пирога.
- Яку частину пирогів з'їли всі гості разом?
Обери правильну відповідь:
А) Вони з'їли 12/10; 10/10; 12/8 частин пирогів.
2. Закріплення вивченого матеріалу.
Вчитель:
Отже, виявляється, що:
1) чисельник дробу може бути меншим за знаменник 9/10, якщо кількість узятих частин менша від кількості частин ділення;
2) чисельник дробу може дорівнювати знаменнику 10, якщо взяти всі частини ділення, тому 10/10 = 1
3) чисельник дробу може бути більшим за знаменник 12/10 (якщо взято не один, а декілька однакових предметів, які поділено на рівну кількість частин і взято кількість частин, більших від тієї, що складають цілий предмет).
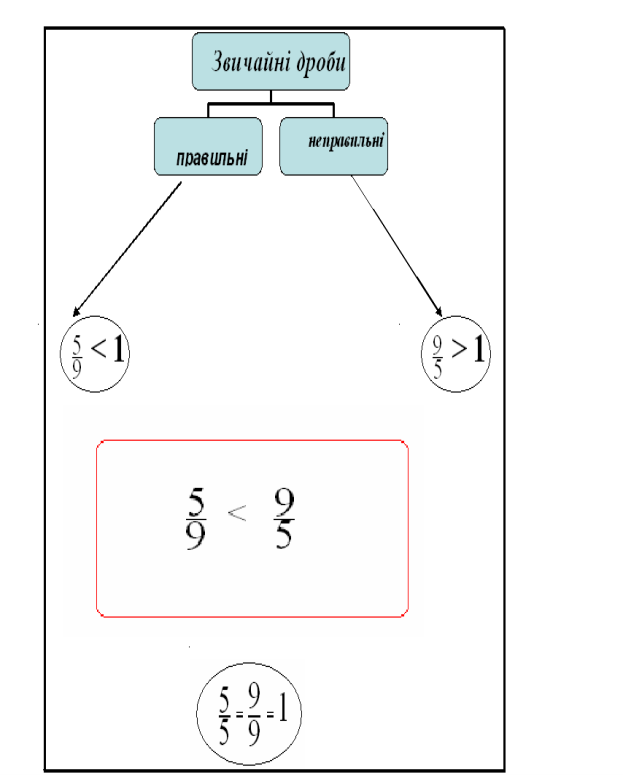
Таблиця на слайді пояснює, що існує класифікація дробів – правильні і неправильні дроби.
Слайд (наочність)
Правильні і неправильні дроби. Порівняння дробів
Правильні дроби: a/b , де а < b; 3/11; 5/17;18/95.
Неправильні дроби: a/b , де а > b; 6/4; 23/12; 102/72.
Порівняння дробів: a/b > c/d, якщо а > с, 7/10 > 6/10, бо 7 > 6;
Робота з підручником
Стор. 220 (правила)
3. Практичне закріплення нового матеріалу. (Слайди)
Усні вправи
1. Які з дробів: 2/3; 5/9; 16/3; 7/26; 19/11;85 /9; є правильними? неправильними?
Вчитель:
Отже, бачимо, що: 1) всі правильні дроби менші за неправильні ( 1/3< 4/3 тощо);
2. Правильний чи неправильний буде дріб y/12,
якщо: 1) у = 10; 2) у = 1; 3) у = 20; 4) у = 12?
Вчитель:
Отже, бачимо, що: 2) всі правильні дроби менші за 1, а неправильні більші або дорівнюють 1;
Фізкультхвилинка
Називаю дріб. Якщо він правильний-то піднімаємо руки вгору, якщо неправильний- то хлопаємо в долоні.
Робота з підручником:
№ 1001,
1007, Робота в парах .Один учень читає дроби, інший записує біля дошки і порівнює, формулюючи правило порівняння дробів. Всі учні побувають біля дошки, або читають дроби (за вибором в парі)
1010
V. Заключний етап
1. Гра «Реальність часу»
Вчитель: До речі, яка частина уроку вже пройшла? Чи встигнемо ми дізнатися на уроці ще щось цікаве?
Учні називають скільки хвилин уроку минуло, залишилось.
Яка частина уроку пройшла? Залишилась? ( Наприклад, ![]() і
і ![]() ).
).
До речі про час: 1хв теж можна записати у вигляді дробу.
1хв = ![]() год.
год.
Ну добре, ми сьогодні почули про Єгипет, Вавілон, а що говорили про звичайні дроби наші предки?
У Київській Русі дроби називали частинами. Найпоширенішими з них були:
![]() - полтинник,
- полтинник, ![]() - четь,
- четь, ![]() - півчеть,
- півчеть, ![]() - треть,
- треть, ![]() - півтреть,
- півтреть, ![]() - півпівтреть.
- півпівтреть.
Накресліть три квадрати із стороною 4 клітини.
(учні виконують побудову в зошиті самостійно, вчитель проходить по класу, допомагає, виправляє помилки).
Заштрихуйте полтинник квадрату, четь квадрата, півчеть квадрата.
Накреслити відрізок 6см . Побудувати треть і півтреть (півпівтреть.)
6 см
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
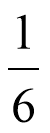
Гра „Хто швидше”
Із чисел 3, 7, 8, 15 скласти усі правильні і неправильні дроби.
2. Домашнє завдання:
1) За підручником: п.30 стор.220. №1008, 1005 , 1011
3. Рефлексія
Використовується метод «Мікрофон». Діти по черзі відповідають на запитання:
Що вам найбільше сподобалося на сьогоднішньому уроці?
Що найбільше запам’яталося?
4. Підсумок уроку. Оцінювання учнів.
Учитель підбиває підсумки уроку, зосереджує увагу учнів на помилках, які вони допускали під час виконання вправ та обчислень.
Найактивніші учні отримують оцінки.
5. Заключне слово вчителя
Вчитель:
Відомий письменник і педагог Лев Толстой вважав, що людина схожа з дробом, знаменник якого є те, що вона думає про себе сама, а чисельник те, що про неї думають інші. Я бажаю всім вам, щоб чисельник у вашому житті завжди був більшим від знаменника.
Думка інших про тебе
Запис на дошці: Людина = -----------------------------
Власна думка про себе
(Л.М.Толстой)


про публікацію авторської розробки
Додати розробку
