Урок «Теорема Пифагора. Обратная теорема Пифагора. Решение задач.»                                                                              8 класс

(используется презентация)

Цель урока:

• закрепить знание теоремы Пифагора и теоремы, обратной теореме Пифагора;
• совершенствовать навыки решения задач на применения этих теорем;
• показать практическое применение теорем;
• развивать смекалку, мышление, математическую речь, память и наблюдательность;
• воспитывать познавательный интерес к предмету.

Тип урока: урок закрепления полученных знаний, умений и навыков.

Формы урока: - фронтальная;

                            - индивидуальная;

                            - самостоятельная.

  Оборудование:

Мультимедиа проектор, ИД, мультимедиа презентация «Теорема Пифагора. Обратная теорема Пифагора. Решение задач.»

Таблицы квадратов натуральных чисел.

«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора»
                              Иоганн Кеплер   

                        Ход урока

І. Организационный момент.

ІІ. Проверка домашнего задания.

ІІІ. Активизация познавательной деятельности урока.

1. Опрос теории:

- в каком треугольнике применима теорема Пифагора;

- как называются стороны прямоугольного треугольника;

- что называется катетом; гипотенузой;

- какая из сторон прямоугольного треугольника является наибольшей;

-каким свойством обладают острые углы прямоугольного треугольника;

- чему равен катет, противолежащий углу 30°?

- сформулируйте теорему Пифагора;

- запишите теорему Пифагора, если катеты прямоугольного    треугольника равны а и   в, а гипотенуза равна  с;

- как по двум сторонам прямоугольного треугольника найти его третью сторону;

- сформулируйте теорему обратную теореме Пифагора;

- для чего используется теорема обратная теореме Пифагора;

- какой треугольник называется египетским?

- для чего мы изучаем теорему Пифагора? Где она применяется?

Где применялась теорема Пифагора? (слайды 4,5)

2. Решить задачи устно: (слайды 6,7).

IV. Обобщение и систематизация знаний и умений.

1. Решить задачи письменно: (слайды 8, 9).

V. Первичный контроль знаний, коррекция.

1.  Взаимоконтроль учащихся (обмениваются выполненной работой и оценивают работу друг друга по уже предложенным вариантам ответов (слайды 11,12,13,13)  

    (Самостоятельная работа  по вариантам прилагается).      

  VI. Подведение итогов.

 Выставление оценок.

VII.  Психологическая разгрузка (рефлексия):  (слайд 15)

         1.Что нового вы узнали на сегодняшнем уроке?

        2. Кто лучше всех работал?

       3. Что понравилось?

VIII. Домашнее задание: (слайд 16)

Спасибо за внимание!

                      Тесты к теме: «Теорема Пифагора. Обратная теорема Пифагора.»                                  Тесты к теме: «Теорема Пифагора. Обратная теорема Пифагора.»

                                 1 вариант                                                                                                                                          2 вариант

1. Дан ∆АВС (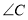=90°); катет АС=5см, а катет ВС= 12 см,                                               1. Дан ∆MNK (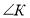=90°).  Катет КМ= 7 см, а  катет KN= 24 см,

тогда гипотенуза АВ равна:                                                                                                    тогда гипотенуза  MN равна:          

А                                                а) 11 см;      б) 13 см;                                                             М                                               а)25см;     б) 9 см;

                                                   в) 8 см;        г) 9.                                                                                                                         в) 14 см;   г) 10 см.

                                                                                               (1,5б.)                                                                                                                                                  (1,5б.)                   

С                                       В                                                                                                       К                                          N   

2. Гипотенуза прямоугольного треугольника 17 см , а один из катетов                    2. Гипотенуза прямоугольного треугольника 13 см, а один из катетов

15 см. Найдите другой катет.                                                                                               12 см. Найдите другой катет.                                

15           17                               а)8 см;  б) 9 см;                                                                        12           13                        а)5 см;   б) 11 см;

                                                   в)10 см; г) 11 см.                                                                                                                 в) 24 см;  г) 16 см.

                                                                                              (1,5б.)                                                                                                                                                    (1,5б.)    

3. Является ли треугольник со сторонами 12 см, 13 см и 4 см прямо-                      3. Является ли треугольник со сторонами 9 см, 40 см и 41 см прямо-

угольным?                                                                            (1б.)                                                 угольным?                                                                                 (1б.)

4. Если диагональ ВD прямоугольника ABCD равна 13 см, а сторона                        4. Если диагональ ВD прямоугольника ABCD равна   25 см, а сторона

АВ = 5 см , то AD равна:                                                                                                           ВС = 20 см, то АВ равна:

            В                                        С               а) 12 см;  б) 8 см;                                                     В               20                     С                   а) 4 см;   б) 11 см;

      5             12                                       в) 21 см;  г)  4 см.                                                                                                                         в)13 см;  г) 15  см.

         А                                        D                                                      (2б.)                                     А                                         D                                                                   (2б.)

  1  вариант                                                                                                                                      2 вариант

5. Если диагонали ромба  BD и AC равны 12 см и 16 см соответственно,                     5. Если сторона ромба ABCD равна 10 см, а диагональ АС = 16 см , то                       то  сторона АВ равна:                                                                                                               диагональ BD равна:

        В                   С           а) 8 см;   б) 6 см;                                                                                                                    В                   С      а) 6 см;  б) 9 см;

                                         в) 10 см; г) 4 см.                                                                                                                                                  в) 12 см;  г) 14 см.

А                    D                                                                    (2б.)                                                                                А                   D                                                  (2б.)

6. Если ABCD(ADIIВС)  – равнобокая трапеция, основания которой                               6. Если ABCD(ADIIВС) – равнобокая трапеция, основания которой

соответственно равны 11 см и 23 см, а боковая сторона АВ равна                              соответственно равны 10 см и 22 см, а высота ВК равна 8 см, то  10см, то высота ВК равна:                                                                                                         CD равна:                   

а) 7 см;    б) 8 см;  в) 24 см;   г) 5 см.                                                                                      а) 7 см;   б) 10 см;   в) 11 см;   г) 15 см.                                                                                                                                                                            

           B        11        C                                                                                                                    B      10          C

      10

                                                                                                                                                                                     D

          А           К      23            D                                                       (2б.)                                     А        K       22              D                                                                         (2б.)