Урок-проект за темою "Використання формул скороченого множення"

Про матеріал

Урок проходить у формі засідання клубу знавців формул скороченого множення. Діти розділені на міні-групи по 4 учні за місцем свого звичайного перебування. Мета уроку: узагальнити, систематизувати та поглибити знання, вміння та навички з використання формул скороченого множення під час розв'язування вправ; розвивати мислення, увагу, спостережливість, пізнавальну активність; виховувати навички самоаналізу, вміння працювати в групах, інтерес до предмета

Перегляд файлу

КЗ «НСЗШ І – ІІІ ступенів №9»

Урок – проект

«Клуб знавців формул»

з алгебри у 7 класі

за темою:

Використання формул
скороченого множення

Підготувала:

вчитель математики

Л.О. Дяченко

м. Нікополь

Мета: узагальнити, систематизувати та поглибити знання, вміння та навички з використання формул скороченого множення під час розв'язування вправ; розвивати мислення, увагу, спостережливість, пізнавальну активність; виховувати навички самоаналізу, вміння працювати в групах, інтерес до предмета

Обладнання: індивідуальні картки, наочність, картки членів клубу

Правило клубу: Знати! Мислити! Досягати мети!

У математиці є своя мова – це мова формул

С.В. Ковалевська

Хід уроку:

Урок проходить у формі засідання клубу знавців формул скороченого множення. Діти розділені на міні-групи по 4 учні за місцем свого звичайного перебування.

Привітання учнів. Промова про форму уроку, клубне правило. Повідомлення теми та мети уроку.
«Клубна картка». Перевірка домашнього завдання. Учні звіряють отримані відповіді з записами на дошці та відмічають правильно виконані завдання у картках членів клубу. Якщо завдання виконані правильно, учні виставляють у персональну картку 2 бали, якщо завдання частково правильне –
1 бал.

Клубна картка уч_______ 7 класу

_________________________________________

Запишіть у вигляді многочлена:

(2b + a) (2b – a) = _________________

(y – 6x) (y + 6x) = _________________

(m⁷ – n⁸) (n⁸ + m⁷) = _______________

(7 – 2x)² = _______________________

(3a – 5) (3a – 5) = _______________

(3 + b) (9 –3b + b²) = _____________

(b + x) (b² – bx + x²) = _____________

(a – 2) (a² + 2a + 4) = _______________

(3 + x) (3 – x) (9 + x²) = _____________

(x² + 1) (x – 1) (x + 1) = _____________

Розкладіть на множники:

p² – c² = _________________________

4a² – 9b² = _______________________

a⁸b⁶ – 25 = _______________________

f³ – d³ = _________________________

27a⁹ + 1000 = _____________________

m² – 2mn + n² = ___________________

4x² – 4x + 1 = _____________________

(m – n)² – b² = _____________________

1 – 100b² = _______________________

100 – 60a + 9a² = ___________________

«Знати = вміти» Учням пропонується, працюючи ланцюжком у міні-групі (передаючи картку) встановити відповідність між умовою завдання та формулою, яку необхідно застосувати для виконання вправи. Кожен наступний учень перевіряє роботу попередника. Учитель перевіряє роботу і за правильні відповіді діти отримають плюс 1 бал.

*Завдання*	*Формула для розв'язання*
16m² – 81n²	a²– b² = (a – b)(a + b)
(x – 9y)(x – 9y)	(a – b)² = a² – 2ab + b²
301 · 299	(a + b)(a – b) = a² – b²
102²	(a + b)² = a² +2ab + b²
x² – 100 = 0	a² – b² = (a – b)(a + b)
(x – 2)(x² + 2x + 4) = x³–x	(a – b)(a²+ ab + b²) = a³ – b³

*Завдання*	*Формула для розв'язання*
100m² – 49	a²– b² = (a – b)(a + b)
(8a – b)(8a – b)	(a – b)² = a² – 2ab + b²
201 · 199	(a + b)(a – b) = a² – b²
999²	(a – b)² = a² – 2ab + b²
x² – 625 = 0	a² – b² = (a – b)(a + b)
(x + 3)(x² – 3x + 9) = x³+x	a³ + b³

*Завдання*	*Формула для розв'язання*
(x – 5)(x² + 5x + 25) = x³–x	(a – b)(a²+ ab + b²) = a³ – b³
1 – x² = 0	a²– b² = (a – b)(a + b)
(2 – 7x) (2 + 7x)	(a – b)(a + b) = a²– b²
(8 – 9x)(8 – 9x)	(a – b)² = a² – 2ab + b²
101 · 99	(a + b)(a – b) = a² – b²
52²	(a + b)² = a² + 2ab + b²

«Обмін досвідом». Учні отримують на міні-групу чотири картки з завданнями та розподіляють картки між собою. Виконують запропоновані завданні у зошиті. І разом заповнюють картки на столі, зазначаючи правильні відповіді та перевіряючи один одного. Звіряють правильність виконання з записами на дошці. За кожну правильну відповідь в індивідуальних завданнях отримують по 1 балу.

Розкладіть на множники
100a⁴ – b²c⁴;

Запишіть у вигляді многочлена
(y – 8x)(y – 8x);

Обчисліть 201 · 199;

Розв'яжіть рівняння
(x – 7)² = x².

Розкладіть на множники
1 + 6a + 9a²;

Запишіть у вигляді многочлена
(b – 5)(b² + 5b + 25);

Обчисліть 49²;

Розв'яжіть рівняння
x² – 10x + 25 = 0.

Розкладіть на множники
(a + 5)² – 81;

Запишіть у вигляді многочлена
(6 + a)(36 – 6a + a²);

Обчисліть 43 · 37;

Розв'яжіть рівняння
(x – 5)² = (x – 3)(x + 3).

Розкладіть на множники
125 + 27x³;

Запишіть у вигляді многочлена
(5 – 3a)(5 + 3a);

Обчисліть 1001²;

Розв'яжіть рівняння
36 – x² = 0.

*Розкладіть на множники*
1) 100a⁴ – b²c⁴ =
2) 1 + 6a + 9a² =
3) (a + 5)² – 81 =
4) 125 + 27x³ =
*Запишіть у вигляді многочлена*
1) (5 – 3a)(5 + 3a) =
2) (y – 8x)(y – 8x) =
3) (b – 5)(b² + 5b + 25) =
4) (6 + a)(36 – 6a + a²) =
*Обчисліть*
1) 201 · 199
2) 1001²
3) 43 · 37
4) 49²
*Розв'яжіть рівняння*
1) (x – 7)² = x²
2) x² – 10x + 25 = 0
3) 36 – x² = 0
4) (x – 5)² = (x – 3)(x + 3)

*Розкладіть на множники*	*Відповіді*
1) 100a⁴ – b²c⁴ =	(10а² – bc²)( 10а² + bc²)
2) 1 + 6a + 9a² =	(1 + 3a) (1 + 3a)
3) (a + 5)² – 81 =	(a – 4)(a + 14)
4) 125 + 27x³ =	(5 + 3x)(25 – 15x + 9x²)
*Запишіть у вигляді многочлена*	*Відповіді*
1) (5 – 3a)(5 + 3a) =	25 – 9a²
2) (y – 8x)(y – 8x) =	y² – 16xy + 64x²
3) (b – 5)(b² + 5b + 25) =	b³– 125
4) (6 + a)(36 – 6a + a²) =	216 + a³
*Обчисліть*	*Відповіді*
1) 201 · 199	39999
2) 1001²	1002001
3) 43 · 37	1591
4) 49²	2401
*Розв'яжіть рівняння*	*Відповіді*
1) (x – 7)² = x²	x = 3,5
2) x² – 10x + 25 = 0	x = 5
3) 36 – x² = 0	x = –6 або x = 6
4) (x – 5)² = (x – 3)(x + 3)	x = 3,4

«Почесний гість». «Професор Форскор» виступає з доповіддю про геометричну інтерпретацію доведення деяких формул скороченого множення та доповнює її доведенням теореми Піфагора з використанням рисунка математика Бхаскара та формул скороченого множення.

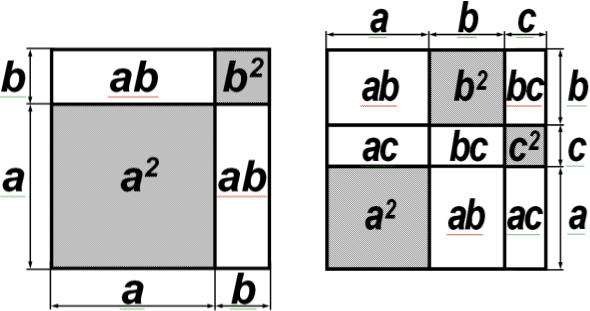
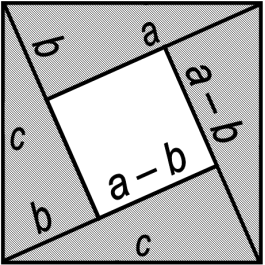
«Суспільна дискусія». Кожна міні-група отримує персональне завдання на доведення подільності. Колективно розв'язує його та передає на перевірку учасникам іншої міні-групи. Картки та розв'язання передаються за годинниковою стрілкою. Учасники іншої міні-групи, перевіривши завдання, презентують його розв'язання на дошці. За правильно розв'язане завдання кожен учасник отримує 2 бали.

Доведіть, що 156² – 144² ділиться на 300

Доведіть, що при довільному цілому значенні n вираз (7n – 2)² – (2n – 7)² ділиться на 5

Доведіть, що при довільному цілому значенні n вираз (7n + 1)² – (2n – 4)² ділиться на 15

Доведіть, що 27² – 14² ділиться на 13

Доведіть, що при довільному цілому значенні n вираз (2n + 7)² – 25
ділиться на 4

Доведіть, що 152² – 48² ділиться на 1600

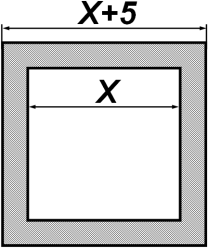
«Розробка рішень до практичних завдань». Учні міні-груп отримують задачі для розв'язання та створюють до них рисунки. Дивлячись на свій рисунок, звіряють його з шістьма запропонованими на дошці та у випадку відповідності забирають собі запропонований. Колективно розв'язують задачу та записують розв’язання до картки. Вивішують на дошку. Звіряють з записами на дошці та презентують коротку доповідь. За правильне розв’язання додають до своїх результатів ще по 3 бали. Якщо учні припустились помилки, учитель пояснює місце її утворення та повідомляє необхідну кількість балів.

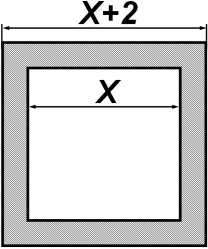
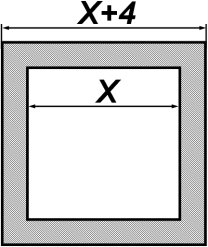
Сторона одного квадрата менша від сторони другого на 2 см,
а різниця їх площ дорівнює 76 см². Знайдіть сторони квадратів.

Нехай х см довжина однієї сторони квадрата, тоді (х + 2) см – довжина другої. Площі квадратів: х² см² та (х + 2)² см². До того ж різниця площ дорівнює 76 см². Складемо і розв'яжемо рівняння:

(х + 2)² – х²= 76;

х² + 4х + 4 – х² = 76;

4х = 72;

х = 18.

Отже, 18 см – сторона одного квадрата, тоді 18 + 2 = 20 (см) – сторона другого квадрата.

Відповідь: 18 см; 20 см.

Сторона одного квадрата менша від сторони другого на 4 см,
а площа – менша на 192 см². Знайдіть периметри кожного квадрата.

Нехай х см довжина однієї сторони квадрата, тоді (х + 4) см – довжина другої. Площі квадратів: х² см² та (х + 4)² см². До того ж різниця площ дорівнює 192 см². Складемо і розв'яжемо рівняння:

(х + 4)² – х²= 192;

х² + 8х + 16 – х² = 192;

8х = 176;

х = 22.

Отже, 22 см – довжина однієї сторони квадрата,
тоді 22 + 4 = 26 (см) – довжина другої сторони квадрата,
22 · 4 = 88 (с) – периметр одного квадрата,

26 · 4 = 104 (см) – периметр другого квадрата.

Відповідь: 88 см; 104 см.

Кожну сторону квадрата збільшили на 0,5 дм, відтак його площа збільшилась на 325 см². Знайдіть площу більшого квадрата.

Нехай х см довжина сторони квадрата. 0,5 дм = 5 см. Тоді (х + 5) см – збільшеної сторони квадрата. Площі квадратів: х² см² та (х + 5)² см².
До того ж різниця площ дорівнює 325 см². Складемо і розв'яжемо рівняння:

(х + 5)² – х²= 325;

х² + 10х + 25 – х² = 325;

10х = 300;

х = 30.

Отже, 30 см – довжина сторони квадрата,
тоді 30 + 5 = 35 (см) – довжина збільшеної сторони квадрата,
S = 35² = 1225 (см²) – площа більшого квадрата.

Відповідь: 1225 см².

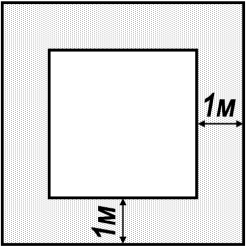
Клумба квадратної форми оточена доріжкою, ширина якої 1 м.
Площа доріжки 20 м². Знайдіть площу клумби.

Нехай х м довжина однієї сторони клумби, тоді (х + 2) м – довжина клумби, оточеної доріжкою. Площі квадратів: х² м² та (х + 2)² м².
До того ж різниця площ дорівнює 20 м². Складемо і розв'яжемо рівняння:

(х + 2)² – х²= 20;

х² + 4х + 4 – х² = 20;

4х = 16;

х = 4.

Отже, 4 м – довжина сторони клумби,
площа клумби S = 4² = 16 (м²).

Відповідь: 16 м².

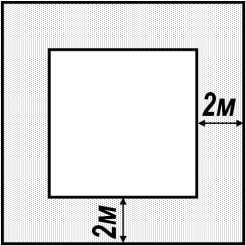
Басейн квадратної форми оточений доріжкою шириною 2 м.
Площа доріжки 88 м². Знайдіть площу басейну.

Нехай х м довжина однієї сторони басейна, тоді (х + 4) м – довжина басейна, оточеного доріжкою. Площі квадратів: х² м² та (х + 4)² м².
До того ж різниця площ дорівнює 88 м². Складемо і розв'яжемо рівняння:

(х + 4)² – х²= 88;

х² + 8х + 16 – х² = 88;

8х = 72;

х = 9.

Отже, 9 м – довжина сторони басейну,
площа басейна S = 9² = 81 (м²).

Відповідь: 81 м².

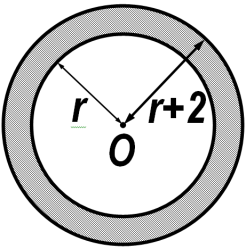
Радіус одного з концентричних кіл більше за інший на 2 см. Знайдіть діаметри цих кіл, якщо різниця площ відповідних кругів дорівнює 36π см²

Нехай r см радіус першого круга , тоді (r + 2) см – радіус другого круга. Площі концентричних кіл: πr² см² та π(r + 2)² см².
До того ж різниця площ дорівнює 36π см². Складемо і розв'яжемо рівняння:

π(r + 2)² – πr²= 36π;

π(r² + 4r + 4 – r²) = 36π;

4r + 4 = 36;

4r = 32;

r = 8.

Отже, 8 см – радіус меншого круга,
тоді 8 + 2 = 10 (см) – радіус більшого круга,
діаметр меншого круга d₁ = 8 · 2 = 16 (см);

діаметр більшого круга d₂ = 10 · 2 = 20 (см).
Відповідь: 16 см; 20 см.

«Таблиця висновків». Підведення підсумку уроку. Учитель вивішує у таблицю найкраще виконані завдання кожного типу та узагальнює з дітьми виконану роботу. Учні підраховують отримані результати роботи та повідомляють результати учителю.

Повідомлення домашнього завдання. Розв'язати завдання з №1.

Література:

Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 7 класс: Учебник для средней общеобразовательной школы.– М.: Просвещение, 1993.– 191с.
Возняк Г.М. Литвиненко Г.М., Мальований Ю.І. Алгебра. 7 клас: Підручник для загальноосвітніх навчальних закладів.– Тернопіль: Навчальна книга – Богдан, 2003. – 192 с.
Гандзій М.Д., Луцків Р.П., Пришляк І.М. Завдання для тематичного контролю з математики. 7 клас. – Тернопіль:СМП»Астон», 2000. – 88с.
Мерзляк А.Г., Полонський В.Б., Рабінович Ю.М., Якір М.С. Збірник задач і завдань для тематичного оцінювання з алгебри для 7 класу. Х.: Гімназія, 2007. – 112 с.

doc

Завантажити

Зберегти на потім

Додав(-ла)

Дяченко Лариса Олександрівна

Пов’язані теми

Алгебра, 7 клас, Розробки уроків

До підручника

Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)

До уроку

Застосування різних способів розкладання многочлена на множники

Додано